Предварительный расчет межосевого расстояния выполняем по формуле 8.13 из учебника для студентов вузов «Детали машин», автор М.Н. Иванов [2].
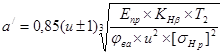 (8.13 [2])
(8.13 [2])
Приведенный модуль упругости: Епр = 2,1*105 МПа.
Коэффициент ширины колеса относительно межосевого расстояния 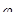 (табл. 8.4 [2]);
(табл. 8.4 [2]); 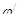 = 0,4.
= 0,4.
Коэффициент концентрации нагрузи при расчетах по контактным напряжениям 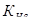 . Рис. 8.15 [2]
. Рис. 8.15 [2]
Чтобы определить значение 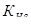 необходимо найти:
необходимо найти:
Коэффициент относительной ширины зубчатого венца относительно диаметра 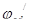
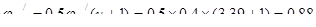 (8.12 [2])
(8.12 [2])
Сравниваем:
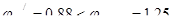 (табл.8.4 [2])
(табл.8.4 [2])
По графику рисунка 8.15 [2] находим: 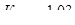
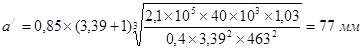
Для нестандартных редукторов межосевое расстояние округляем по ряду Ra40 ([2] стр. 136). Принимаем а = 80 мм.
Определяем модуль передачи
Модуль передачи определяем по формуле:  (8.15 [2])
(8.15 [2])
где:
вw - ширина зубчатого венца:  (8.16 [2]), это значение соответствует стандартному ряду линейных размеров.
(8.16 [2]), это значение соответствует стандартному ряду линейных размеров.
Коэффициент, учитывающий влияние ширины колеса, 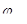
Принимаем 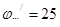 (табл.8.5 [2]).
(табл.8.5 [2]).
m/ = 32/25 = 1,28 мм
По табл.8.1. [2] приводим найденное значение модуля к стандартному m = 1,5 мм
Определяем число зубьев шестерни и колеса
6.1 Суммарное число зубьев шестерни и колеса определяем по формуле:
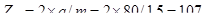 ([1], стр.31)
([1], стр.31)
6.2 Число зубьев шестерни:
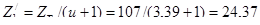 ([1], стр.31)
([1], стр.31)
Принимаем Z1 = 25 ≥ Zmin = 17
6.3 Число зубьев колеса:
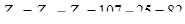 ([1], стр.31)
([1], стр.31)
Уточняем передаточное число
Определяем фактическое передаточное число по формуле:
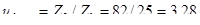
Погрешность значения фактического передаточного числа от номинального значения:
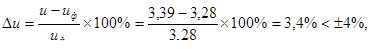 что допустимо даже для стандартных редукторов ([2], стр.137).
что допустимо даже для стандартных редукторов ([2], стр.137).
За передаточное число редуктора принимаем u = 3,28.
8. Определяем основные геометрические размеры
шестерни и колеса
8.1 Определяем делительные диаметры
Шестерни: d1 = z1 x m = 25 x 1,5 = 37 мм
Колеса: d2 = z2 x m = 82 x 1,5 = 123 мм
8.2 Определяем диаметры вершин зубьев
Шестерни: dа1 = d1 + 2 x m = 37 + 2 x 1,5 = 40 мм
Колеса: dа2 = d2 + 2 x m = 123 + 2 x 1,5 = 126 мм
8.3 Определяем диаметры впадин
Для прямозубых цилиндрических передач:
Шестерня: df1 = d1 – 2,5 x m = 37 – 2,5 x 1,5 = 33 мм
Колесо: df2 = d2 – 2,5 x m = 123 – 2,5 x 1,5 = 119 мм
8.4 Определяем высоту зуба
h = 2,25 x m = 2,25 x 1,5 = 3,4 мм
8.5 Определяем ширину венца шестерни и колеса
в1 = вw = 32 мм
в2 = 1,1 х вw = 35,2 мм
Принимаем 36 мм.
8.6 Проверяем величину межосевого расстояния
aw = 0,5 (d1 + d2) = 0,5 (37 + 123) = 80 мм (8.1 [2])
Корригирования зубьев не требуется.
Сводная таблица параметров прямозубого цилиндрического зацепления без смещения
Параметры зацепления
Числовые значения
Модуль, m
1,5
Межосевое расстояние, а
80
Нормальный исходный контур, α
20
Высота зуба, h
3,4
Шестерня
Колесо
Геометрические параметры
Число зубьев, z2
Ширина венца, в2
Делительный диаметр, d2
Диаметр вершин зубьев, da2
Диаметр впадин зубьев, df2
9. Проверка зубьев на выносливость
по контактными напряжениям
9.1 Определяем коэффициент расчетной нагрузки
Кн = Кнβ х Кнv ([2] стр.127)
Ранее было найдено: Кнβ =1,03
Для того, чтобы найти коэффициент динамической нагрузки по контактным напряжениям Кнv необходимо определить окружную скорость ведомого вала
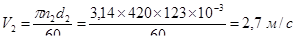
Учитывая, что V2 = 2,7 м/сек, по табл. 8.2 [2] назначаем 8ую степень точности.
Далее по таблице 8.3 [2] находим Кнv = 1,11
Кн = 1,03 х 1,11 = 1,1433
9.2 Определяем расчетные контактные напряжения по формуле 8.10 [2]
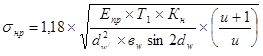 , где
, где
dw/ = d1 = 37 мм αw = α =20˚
вw = 32 мм sin2αw = 0,64
Крутящий момент на ведущем валу:
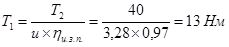
 - КПД закрытой цилиндрической передачи
- КПД закрытой цилиндрической передачи
По рекомендации параграфа 8.1 [2] для восьмой степени точности:
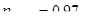
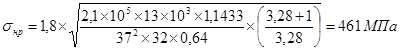
Дата: 2019-12-22, просмотров: 401.