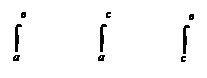 Теорема 1. Пусть с – промежуточная точка интервала [а,в] (а < с < в). Тогда имеет место равенство
Теорема 1. Пусть с – промежуточная точка интервала [а,в] (а < с < в). Тогда имеет место равенство
f(х)dх = f(х)dх + f(х)dх,
если все эти три интеграла существуют.
Доказательство: Разобьём [
а,в] на
п частичных интервалов [
а,х1], [
х1,х2], …, [
хп–1,
в] длиной соответственно D
х1, D
х2, …, D
хп так, чтобы точка
с была точкой деления. Пусть, например,
хт =
с (
т <
п). Тогда интегральная сумма
å f(a i)Dхi
соответствующая интервалу [
а,в], разобьётся на две суммы:
å f(a i)Dхi = å f(a i)Dхi = å f(a i)Dхi
соответствующие интервалам [а,с] и [с,в].
Переходя к пределу при неопределённом уменьшении длины максимального частного интервала Dхi, то есть, при max Dхi ® 0, будем иметь
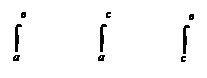 f(х)dх = f(х)dх + f(х)dх,
f(х)dх = f(х)dх + f(х)dх,
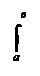
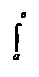 Теорема 2. Постоянный множитель можно выносить за знак определённого интеграла, то есть
Теорема 2. Постоянный множитель можно выносить за знак определённого интеграла, то есть
k f(х)dх = k f(х)dх.
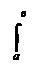 Доказательство: По определению:
Доказательство: По определению:
k f(
х)
dх = lim [
k f(
a1)D
х1 +
k f(
a2)D
х2 + … +
k f(
a п)D
хп] =
=
lim å
k f(
a i)D
хi.
Но так как, согласно одному из свойств предела,
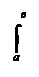
lim å
k f(
a i)D
хi = k lim å
f(
a i)D
хi,

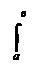
и так как, по определению,
lim å
f(
a i)D
хi = f(х)dх
то
k f(х)dх = k lim å
f(
a i)D
хi = k f(х)dх
Теорема 3. Определённый интеграл от алгебраической суммы нескольких непрерывных функций равен алгебраической сумме определённы интегралов от этих функций.
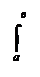
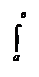

 Доказательство: Докажем, например, что
Доказательство: Докажем, например, что
[f1(х) + f2(х) – f3(х)]dх = f1(х)dх + f2(х)dх – f3(х)dх
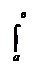
в самом деле имеем:
[
f1(
х) +
f2(
х) –
f3(
х)]
dх =
lim å [
f1(
a i)
dх +
f2(
a i)
dх –
f3(
a i)]D
хi =
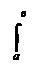
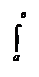
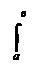
= lim å
f1(
a i)D
хi +
lim å
f2(
a i)D
хi –
lim å
f3(
a i)D
хi =
= f1(х)dх + f2(х)dх – f3(х)dх
Теорема 3. (о среднем значении определённого интеграла)
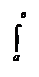 Если функция f(х) непрерывна на [а,в], то внутри него найдётся такая точка С.
Если функция f(х) непрерывна на [а,в], то внутри него найдётся такая точка С.
f(х)dх = (в–а) f(с)
Доказательство: Так как функция f(х) непрерывна на [а,в], то она достигает своего наибольшего и наименьшего значений М и т на [а,в]. произведём обычное разбиение интервала [а,в], на п частичных интервалов Di длиной Dхi = х f(a i) ³ т – хi–1 (i = 1, …, п).
Так как f(a i) ³ т при любом a i, то
f(
a i)D
хi ³
т D хi
откуда å
f(
a i)D
хi ³
т å D
хi
или å
f(
a i)D
хi ³
т(
в – а)
так как å Dхi = Dх1+Dх2 + … + Dхп = в – а.
Так как, далее, f(a i) £ т, при любом a i , то
f(
a i)D
хi £
МD
хi
а потому å
f(
a i)D
хi £
М åD
хi,
то есть, å f(a i)Dхi £ М(в – а).
Таким образом, имеем
т(в – а) £ å f(a i)Dхi £ М(в – а).
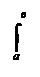 Переходя к пределу при max Dхi ® 0, получим неравенства
Переходя к пределу при max Dхi ® 0, получим неравенства
т(в – а) £ f(х)dх £ М(в – а)
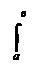
f(х)dх
(в – а)
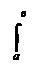 Из этих неравенств и теореме о непрерывной функции на [а,в], принимающей в этом [а,в] все промежуточные значения между своими наибольшими и наименьшими значениями, следует, что отношение
Из этих неравенств и теореме о непрерывной функции на [а,в], принимающей в этом [а,в] все промежуточные значения между своими наибольшими и наименьшими значениями, следует, что отношение
f(х)dх
(в – а)
можно принять за значение f(с) функции f(х) в некоторой промежуточной точке с интервала [а,в] (т £ f(с)£ М).
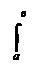 Таким образом,
Таким образом,
( f(х)dх) / (в – а) = f(с)
или
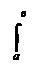 f(х)dх = (в – а)f(с)
f(х)dх = (в – а)f(с)
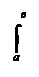 2.9. Геометрический смысл определённого интеграла.
2.9. Геометрический смысл определённого интеграла.
Известно, что площадь криволинейной трапеции, ограниченной сверху непрерывной кривой
у =
f(
х), снизу – интервалом [
а,в] оси О
х (
а £
х £
в) и с боковых сторон – прямыми
х =
а, х = в, равна
S =
lim å
f(
a i)D
хi
Но, по определению,
f(
х)
dх =
lim å
f(
a i)D
хi
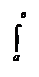 следовательно,
следовательно,
S = f(х)dх
Таким образом, в случае, когда f(х) ³ 0, то есть, когда график функции у = f(х) располагается над осью Ох, определённый интеграл численно равен площади S криволинейной трапеции.
Если же f(х) = 0 при а £ х £ в, то есть если кривая располагается под осью Ох, то сумма
å
f(
a i)D
хi
 равна сумме площадей криволинейной трапеции аАВв, взятой со знаком минус (рис. 4)
равна сумме площадей криволинейной трапеции аАВв, взятой со знаком минус (рис. 4)
Тогда с геометрической точки зрения определённый интеграл от f(х)dх численно равен площади S криволинейной трапеции, ограниченной интервалом [а,в] оси Ох (а £ х £ в), непрерывной кривой у = f(х) и отрезками прямых х = а, х = в, равными f(а) и f(в).
Теорема Ньютона–Лейбница.
Пусть функция f непрерывна на [а,в]. тогда она интегрируема на любом отрезке, [а,х], где а £ х £ в, то есть, для любого х Î [а,в], существует интеграл
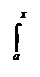 F(х) = f(t)dt (V)
F(х) = f(t)dt (V)
Если f(t)³0 " tÎ[а,в], то F(х) = S(х), где S(х) – площадь криволинейной трапеции аАL(х) (рис. 5)
Определение. Функция F определённая соотношением (V) на [
а,в] называется интегралом с переменным верхним пределом.
Эта функция непрерывна и дифференцируема на [а,в]. А именно имеет место следующая теорема.
Теорема. (Ньютона–Лейбница)
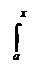
Производная определённого интеграла от непрерывной на [
а,в] функции
f , рассматриваемого как функция его верхнего предела, существует и равна значению подынтегральной функции в точке дифференцирования.
F’(х) = ( f(t)dt) = f(х)1, х Î [а,в] .
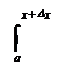

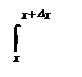 Доказательство: Пусть х Î [а,в], х + Dх Î [а,в]; тогда в силу теоремы 1 пункта 2.12. получим
Доказательство: Пусть х Î [а,в], х + Dх Î [а,в]; тогда в силу теоремы 1 пункта 2.12. получим
F(х + D х) = f(t)dt = f(t)dt + f(t)dt
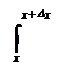 Найдём соответствующее приращение DF функции F. Используя равенства (V) и теорему 4 пункта 2.12. имеем
Найдём соответствующее приращение DF функции F. Используя равенства (V) и теорему 4 пункта 2.12. имеем
DF = F(х + D х) – F(х) = f(t)dt = f(с) D х, где
с Î [х, х + D х]
Вычислим производную функции (V):
F’(
х) =
lim =
lim = lim f(с)
Если Dх ® 0, то х + Dх ® 0 и с ® х, так как с Î [х, х+ D х]. Тогда в силу непрерывности f получим
F’(
х) =
lim f(с) = f(х)
Что и требовалось установить.
Легко вытекает следующее утверждение: всякая непрерывная на [а,в] функция имеет на этом отрезке первообразную при этом одной из первообразных является интеграл (V).
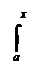
Действительно, пусть функция
f непрерывна на [
а,в]; тогда она интегрируема на любом на [
а,х], где
х Î [
а,в], то есть, существует интеграл (V), который и является первообразной функцией для
f . Следовательно, неопределённый интеграл от непрерывной на [
а,в] функции
f можно записать в виде
f(х)dх = f(t)dt + С, х Î [а,в]
где С – произвольная постоянная.
Формула Ньютона–Лейбница.
Теорема. Если Ф – первообразная для непрерывной на [а,в] функции f, то определённый интеграл от функции f вычисляется по формуле
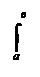 f(х)dх = Ф(в) – Ф(а).
f(х)dх = Ф(в) – Ф(а).
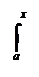 Доказательство: Пусть Ф некоторая первообразная для функции f . В силу предыдущей теоремы функция (V) также является первообразной для функции f . Поскольку две первообразные Ф и F отличаются друг от друга на некоторую постоянную, имеем
Доказательство: Пусть Ф некоторая первообразная для функции f . В силу предыдущей теоремы функция (V) также является первообразной для функции f . Поскольку две первообразные Ф и F отличаются друг от друга на некоторую постоянную, имеем
f(х)dх = Ф(х) + С (1)
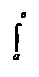 Положим в последнем равенстве х = а. Так как
Положим в последнем равенстве х = а. Так как
f(х)dх = 0,
то Ф(а) + С = 0, откуда С = – Ф(а)
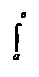 Подставляя найденное значение С в соотношение (1), имеем
Подставляя найденное значение С в соотношение (1), имеем
f(х)dх = Ф(х) – Ф(а).
Полагая в последнем соотношении х = в и обозначая переменную t через х, окончательно получим равенство указанное в теореме.
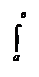
Формулу Ньютона–Лейбница в сокращённом виде принято записывать так:
f(х)dх = Ф(х)| = Ф(в) – Ф(а)
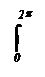 Примеры.
Примеры.
1)
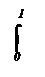 sin хdх = – cos х| = – cos 2 p + cos 0 = 0.
sin хdх = – cos х| = – cos 2 p + cos 0 = 0.
2) 
 = ln |x + x2+1| = ln (1+Ö2) – ln 1 = ln (1+Ö2)
= ln |x + x2+1| = ln (1+Ö2) – ln 1 = ln (1+Ö2)
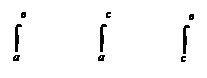 Теорема 1. Пусть с – промежуточная точка интервала [а,в] (а < с < в). Тогда имеет место равенство
Теорема 1. Пусть с – промежуточная точка интервала [а,в] (а < с < в). Тогда имеет место равенство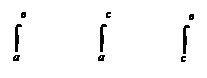 f(х)dх = f(х)dх + f(х)dх,
f(х)dх = f(х)dх + f(х)dх,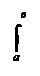
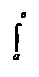 Теорема 2. Постоянный множитель можно выносить за знак определённого интеграла, то есть
Теорема 2. Постоянный множитель можно выносить за знак определённого интеграла, то есть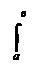 Доказательство: По определению:
Доказательство: По определению: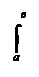

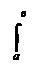
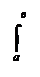
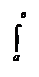

 Доказательство: Докажем, например, что
Доказательство: Докажем, например, что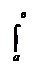 в самом деле имеем:
в самом деле имеем:
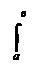
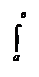
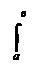
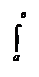 Если функция f(х) непрерывна на [а,в], то внутри него найдётся такая точка С.
Если функция f(х) непрерывна на [а,в], то внутри него найдётся такая точка С.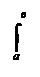 Переходя к пределу при max Dхi ® 0, получим неравенства
Переходя к пределу при max Dхi ® 0, получим неравенства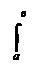
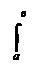 Из этих неравенств и теореме о непрерывной функции на [а,в], принимающей в этом [а,в] все промежуточные значения между своими наибольшими и наименьшими значениями, следует, что отношение
Из этих неравенств и теореме о непрерывной функции на [а,в], принимающей в этом [а,в] все промежуточные значения между своими наибольшими и наименьшими значениями, следует, что отношение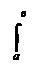 Таким образом,
Таким образом,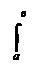 f(х)dх = (в – а)f(с)
f(х)dх = (в – а)f(с)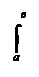 2.9. Геометрический смысл определённого интеграла.
2.9. Геометрический смысл определённого интеграла.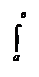 следовательно,
следовательно, равна сумме площадей криволинейной трапеции аАВв, взятой со знаком минус (рис. 4)
равна сумме площадей криволинейной трапеции аАВв, взятой со знаком минус (рис. 4)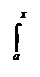 F(х) = f(t)dt (V)
F(х) = f(t)dt (V)
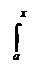
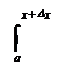

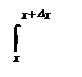 Доказательство: Пусть х Î [а,в], х + Dх Î [а,в]; тогда в силу теоремы 1 пункта 2.12. получим
Доказательство: Пусть х Î [а,в], х + Dх Î [а,в]; тогда в силу теоремы 1 пункта 2.12. получим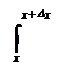 Найдём соответствующее приращение DF функции F. Используя равенства (V) и теорему 4 пункта 2.12. имеем
Найдём соответствующее приращение DF функции F. Используя равенства (V) и теорему 4 пункта 2.12. имеем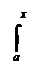 Действительно, пусть функция f непрерывна на [а,в]; тогда она интегрируема на любом на [а,х], где х Î [а,в], то есть, существует интеграл (V), который и является первообразной функцией для f . Следовательно, неопределённый интеграл от непрерывной на [а,в] функции f можно записать в виде
Действительно, пусть функция f непрерывна на [а,в]; тогда она интегрируема на любом на [а,х], где х Î [а,в], то есть, существует интеграл (V), который и является первообразной функцией для f . Следовательно, неопределённый интеграл от непрерывной на [а,в] функции f можно записать в виде
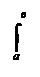 f(х)dх = Ф(в) – Ф(а).
f(х)dх = Ф(в) – Ф(а). 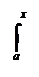 Доказательство: Пусть Ф некоторая первообразная для функции f . В силу предыдущей теоремы функция (V) также является первообразной для функции f . Поскольку две первообразные Ф и F отличаются друг от друга на некоторую постоянную, имеем
Доказательство: Пусть Ф некоторая первообразная для функции f . В силу предыдущей теоремы функция (V) также является первообразной для функции f . Поскольку две первообразные Ф и F отличаются друг от друга на некоторую постоянную, имеем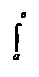 Положим в последнем равенстве х = а. Так как
Положим в последнем равенстве х = а. Так как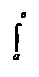 Подставляя найденное значение С в соотношение (1), имеем
Подставляя найденное значение С в соотношение (1), имеем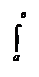 Формулу Ньютона–Лейбница в сокращённом виде принято записывать так:
Формулу Ньютона–Лейбница в сокращённом виде принято записывать так:
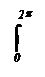 Примеры.
Примеры.
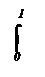 sin хdх = – cos х| = – cos 2 p + cos 0 = 0.
sin хdх = – cos х| = – cos 2 p + cos 0 = 0.

 = ln |x + x2+1| = ln (1+Ö2) – ln 1 = ln (1+Ö2)
= ln |x + x2+1| = ln (1+Ö2) – ln 1 = ln (1+Ö2)