Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Пусть интервал [а,в], на котором задана функция у = f(х), разбит точками деления х₁< х₂ < … < х_{п – 1} на п частичных интервалов D₁ = [х₀,х₁], D₂ = [х₁,х₂], …, D_n = [х_п–1,х_п], где а =х₀ , в = х_п, причём в каждом частичном интервале D_i выбрана какая–либо точка a_i:

х_i–1 £ a_i £ х_i (i = 1, 2, …, п). Пусть, далее, Dх_i – длина интервала D_i , то есть,

                 х_i – х_i–1 = Dх_i  (i = 1, 2, …, п),

а max Dх_i – наибольшее из чисел Dх_i.

п i=1

Требуется найти предел суммы

(1) f(a₁) Dх₁ + f(a₂) Dх₂ + … + f(a _п) Dх_п = å f(a _i) Dх_i,

когда длины Dх_i всех частичных интервалов D_i стремятся к нулю (при этом с необходимостью число п этих интервалов будет стремиться к бесконечности). Другими словами, требуется найти предел этой суммы при max Dх_i ® 0, так как условие, что максимальная из длин частичных интервалов D_i стремится к нулю, равносильно условию, что все Dх_i ® 0.

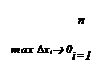Итак, требуется найти

                 lim å f(х_i) Dх_i.

Определение.  Сумму (1) называют интегральной суммой.

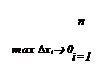Определение. Функция f(х) называется интегрируемой на интервале [а,в], если существует конечный предел       

                 lim å f(a _i) Dх_i, (2)

                 не зависящий от того, каким образом интервал [а,в] делится на частичные интервалы и каким образом выбираются точки a _i на этих частичных интервалах, лишь бы длина максимального из них стремилась к нулю. Этот предел называется определённым интегралом от функции f(х) на интервале [а,в] и обозначается символом

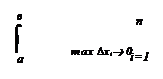                 f(х)dх = lim å f(a _i) Dх_i.

Для того чтобы не оставалось неясностей, сформулируем точно, как следует понимать предел (2).

п i=1

Определение. Число J называется пределом интегральной суммы å f(a _i)Dх_i при max Dх_i ® 0, если для любого заданного e > 0 найдётся такое d > 0, что выполняется неравенство:

                 |å f(a _i)Dх_i – J |< e

                 при любом выборе частных интервалов, D₁, D₂, …, D_п и точек a₁, a₂, …, a _п на этих интервалах, лишь бы только выполнялось требование max Dх_i ® 0, то есть лишь бы длина наибольшего (а значит, и всех) из частичных интервалов была меньше d.

Из определения определённого интеграла отнюдь не следует, что любая функция интегрируема на любом интервале. Можно подобрать такие функции, для которых определённый интеграл не существует, то есть для которых интегральная сумма не стремится к определённому пределу. Существование определённого интеграла от функции, заданной на интервале [а,в], обеспечивает непрерывность этой функции на [а,в], поэтому непрерывность функции на [а,в] является достаточным условием её интегрируемости на этом интервале, то есть

Теорема 1. Если функция f(х) непрерывна на замкнутом интервале [а,в], то она интегрируема на этом интервале, то есть имеет определённый интеграл

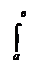                 f(х)dх.  

Иногда на практике приходится интегрировать и разрывные функции. Приведём несколько более широкое достаточное условие существования интеграла.

Теорема 2. Если на интервале [а,в] функция ограничена и имеет лишь конечное число точек разрыва, то она интегрируема на [а,в].