Для долговременного периода актуальными являются понятия общих и средних издержек, и здесь уже невозможно деление их на постоянные и переменные. Все издержки предприятия (фирмы) являются переменными.
SA Т C
LA Т C

SA Т C 1 SA Т C 5 SA Т C 1
А SA Т C 2 SA Т C 4
 В С SA Т C 3 D LA Т C
В С SA Т C 3 D LA Т C
Q
0 Q1 Q2 Q3 Q4
Рисунок 18. Кривая долгосрочных средних издержек.
На рисунке 18 показана кривая долгосрочных средних общих издержек (LАТС), которая состоит из участков кривых краткосрочных издержек (SАТС1, SАТС2 и т.д.) применительно к различным размерам тех предприятий, которые могут быть построены. Эти варианты фирма может рассматривать как ступени своего роста. На каких-то промежутках своей деятельности фирма не меняет производственные мощности, а использует то, что имеет, т. е. можно допустить, что на каждой ступени фирма функционирует в краткосрочном периоде (S). Поэтому кривая, описывая ее издержки на данном этапе, будет кривой краткосрочных средних издержек. Кривая S АТС1 описывает краткосрочные средние издержки для самого малого предприятия (1-й вариант). это значит, что предприниматель ставит цель получить объем продукции, не превышающий Q1 единиц. Но этот объем продаж может быть произведен и на большем предприятии, но тогда увеличатся средние общие издержки, поскольку увеличиваются производственные мощности. Выбор второго варианта размера предприятия предполагает расширение объема выпуска от Q1 до Q2 единиц продукции и т. д. Каждой точке на кривой долгосрочных средних издержек (L АТС) соответствует конкретный размер предприятия со своей собственной кривой S АТС. Кривая долгосрочных средних издержек L АТС (плановая кривая, или кривая-конверт) является касательной (огибающей) для всех возможных кривых краткосрочных S АТС. Она показывает наименьшие издержки на производство единицы продукции, с которыми может быть обеспечен любой объем производства при условии, что предприятие имело в своем распоряжении достаточно времени для проведения необходимых изменений в размерах предприятия. Следовательно, фирма определяет максимальный объем производства при наименьших издержках. На рис. 18 видно, что наращивание производственных мощностей предприятия будет сопровождаться уменьшением средних общих издержек на производство единицы продукции вплоть до достижения размеров предприятия, соответствующих S АТС3. Дальнейшее наращивание объема производства стремится к увеличению долгосрочных средних общих издержек. Дугообразную форму кривой L АТС можно объяснить с помощью эффекта масштаба. Выделяют положительный, нейтральный и отрицательный эффекты.
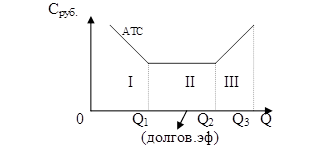
Рисунок 19. Изменение в масштаб производства (эффект масштаба).
Кривая долгосрочных издержек состоит из вариантов, которые называются ступени роста. В каждой ступени (I – III) фирма функционирует в краткосрочном периоде. Динамику кривой долгосрочных издержек (LATC) можно объяснить при помощи эффекта масштаба. Изменение фирмой параметров своей деятельности, т.е. переход от одного варианта размеров предприятия к другому получил название изменение в масштабе производства.
| I – на этом временном интервале долгосрочные издержки снижаются с увеличением объёма выпускаемой продукции, т.е. имеет место экономия от роста масштаба – положительный эффект масштаба (от 0 до Q1). |
| II – (это от Q1 до Q2), на этом временном интервале производства долгосрочные АТС не реагируют на увеличение объёма производства, т.е. остаются неизменным. И фирма будет иметь постоянный эффект от изменения масштаба производства (постоянная отдача от роста масштаба – нейтральный эффект). |
| III – долгосрочные АТС при увеличении объёма выпуска растут и имеет место ущерб от роста масштаба производства или отрицательный эффект масштаба (от Q2 до Q3). |
9. Понятие изокосты. Равновесие товаропроизводителя.
| ·Изокоста – это линия равных издержек при различных сочетаниях труда и капитала (рис. 19). |
В качестве переменных факторов выступают труд L (фактор Х) и капитал К (фактор Y). Цены труда и капитала постоянны (Px, Py = const). Изокоста (С) или бюджетное ограничение производителя (денежные средства, которыми располагает фирма для организации производства) определяется по следующей формуле:
| ТC = PK × k + PL × L |
(1)
(1)
где, PK, – цена одной единицы капитала;
PL – цена одной единицы труда.
К – капитал;
L – труд.
Поскольку PL = W (заработная плата) и PK= r (арендная плата за капитал):
·бюджетное ограничение производителя можно записать также при помощи следующей формулы:
ТС= WL + r К, (2) (2)
где,ТС-валовые издержки (инвестиционный бюджет);
WL- издержки на оплату труда;
rК – капитальные издержки.
| ·Для каждого значения валовых издержек существует своя изокоста. |
Если переписать уравнение (2) как уравнение для прямой линии, то получим:
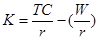 L L
|
(3)
Отсюда, угол наклона изокосты =| 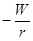 |, но поскольку
|, но поскольку
PL = W и PK= r ,
то угол наклона изокосты можно выразить 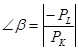 , через цены на переменные ресурсы (К) и (L).
, через цены на переменные ресурсы (К) и (L).
·Отсюда угловой коэффициент изокосты:
| 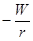 | = |
| = | 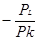 |.
|.
·Угловой коэффициент изокосты показывает :
–угол наклона изокосты;
–что при замене капитала на труд, либо труда на капитал ТС (валовые издержки) остаются неизменными (ТС= const ).

Рисунок 20. Изокоста.
·Равновесие производителя
Допустим фирме необходимо произвести определенное количество продукции равное Q1.Совместим карту изокост (ТС1, ТС2,) доступную по бюджету фирме, с изоквантой (Q 1), указав точку касания (В). Определим оптимальный объем производства при заданных бюджетных возможностях. В точке (В) (рис. 20) угол наклона изокосты 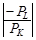 равен углу наклона изокванты
равен углу наклона изокванты 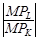 , где МРк – предельный продукт капитала, МРL – предельный продукт труда. Поскольку в точке (В), ТС1 <ТС2, на которой лежат точки А и С (рис. 21) , а угол наклона β изокосы и изокванты в точке (В) совпадают, то точка (В) является оптимальной для производителя. Точки (А) и (С) неэффективны, поскольку в них производителю необходимо было бы для производства Q1 единиц продукции затратить больше средств (ТС2>ТС1).
, где МРк – предельный продукт капитала, МРL – предельный продукт труда. Поскольку в точке (В), ТС1 <ТС2, на которой лежат точки А и С (рис. 21) , а угол наклона β изокосы и изокванты в точке (В) совпадают, то точка (В) является оптимальной для производителя. Точки (А) и (С) неэффективны, поскольку в них производителю необходимо было бы для производства Q1 единиц продукции затратить больше средств (ТС2>ТС1).
К


 А
А

В С Q1
 β
β
 0 ТС1 ТС2 L
0 ТС1 ТС2 L
Рисунок 21. Равновесие (оптимум) производителя
·Равновесие производителя находится в точке (В), поскольку фирма, производя одно и то же количество товара в точках А, В и С, выбирает в точке (В) наименьшие издержки ТС1. Точка касания изокосты и изокванты (В) определяет оптимальный набор факторов К и L (Рис.21).
| ·Точка (В) отражает состояние оптимума производителя, когда последний рубль, затраченный на каждый ресурс, приносит одинаковый предельный продукт. |
Математически система равновесий описывается следующей системой уравнений:
Т 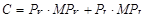
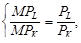
·отсюда
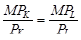
|
Это и есть условие оптимума производителя или правило минимизации издержек.
Траектория роста фирмы
·При наложении карты изоквант на курту изокост можно получить траекторию роста фирмы (линию ОК) или изоклиналь (рис. 22).
Изоклиналь показывает оптимальные объемы производства фирмы при разных производственных мощностях.


Рисунок 22. – Траектория экономической деятельности фирмы (изоклиналь).
Дата: 2019-12-22, просмотров: 408.