Метод групповых проверок заключается в том, что путем проверки одного или нескольких параметров определяется часть изделия, в которой находится неисправный элемент, затем проводится другая серия проверок, позволяющая выявить следующую подгруппу элементов, включающую в себя неисправный элемент, и так далее до тех пор, пока последний не будет локализован и однозначно определен.
Если исходные данные по надежности элементов отсутствуют, то наиболее приемлемым методом поиска отказавшего элемента является метод половинного разбиения. Сущность метода заключается в том , что участок схемы с последовательно соединенными элементами делится на две равные части и равнозначно выбирается для проверки левая или правая ветвь. Если в результате проверки, например левой части схемы, окажется, что неисправный элемент находится в правой ветви, то для локализации отказавшегося элемента правая ветвь дополнительно делится на два равнозначных участка. Такое деление будет продолжаться до тех пор, пока не будет обнаружен отказавший элемент. Критерий половинного разбиения учитывает только одну из характеристик проверок – число элементов, охваченных проверкой. Он может дать оптимальное решение только при равных вероятностях отказов элементов и одинаковом времени проверок групп. Поскольку надежность элементов, входящих в систему, может отличатся, лучше использовать метод разбиения последовательной системы на две части с равными суммарными вероятностями отказа или интенсивностями отказов. Для практического использования метода вводят следующие ограничения: в системе может отказать только один элемент, время проверок различных групп элементов одинаково. В этом случае в качестве критерия оптимальности при проведении диагноза можно использовать выражение [Р(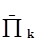 
) ] = min, где Р( 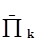) – вероятность отрицательного исхода,
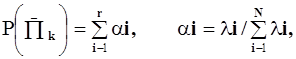(3.1)
где r- число элементов, охваченных проверкой.
Подсчитав значение Р(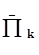 
) для всех проверок и используя предложенный критерий, можно выбрать место первой проверки. После проведения первой проверки схема разбивается на две части, которые рассматриваются как самостоятельные объекты. Для каждого из них определяются коэффициенты отказа a (сумма коэффициентов отказа должна быть равна 1), составляется перечень возможных проверок и выбирается проверка, для которой вероятности исходов близки к 0,5. Указанный процесс продолжается до однозначного определения отказавшего элемента.
3.3 Решение типовых примеров
Пример 1. Система автоматического управления технологическим процессом состоит из 14 элементов, соединенных в структурной схеме надежности последовательно (рис. 4.1)
Рис. 3.1. Структурная схема надежности системы автоматического управления
Выход каждого из элементов приводит к отказу системы. Заданы интенсивности отказов элементов (li × 10-5 ч-1)
l1 =7, l2 =3, l3 =4, l4 =5, l5 =4, l6 =5, l7 =6, l8 =1, l9 =1, l10 =2, l11 =1, l12 =2, l13 =2, l14 =1
Время поиска отказавшего элемента одинаково для всех проверок и составляет 5 мин. Используя метод последовательных поэлементных проверок, установить оптимальную последовательность диагностирования системы управления.
Решение. 1. Определяем суммарную интенсивность отказов системы
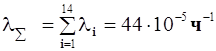
4. По формуле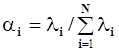 
находим значение показателя a i для всех элементов, в результате получаем a 1 = 0,16, a 2 = 0,068, a 3 = 0,09, a 4 = 0,11, a 5 = 0,09, a 6 = 0,11, a 7 = 0,136, a 8 = 0,022, a 9 = 0,022, a 10 = 0,045, a 11 = 0,022, a 12 = 0,045, a 13 = 0,045, a 14 = 0,022.
5. Определяем отношение a i / ti , с учетом того, что ti = t = 5 мин
a1 / t = 0,032, a2 / t = 0,0136, a3 / t = 0,018, a4 / t = 0,022, a5 / t = 0,018, a6 / t = 0,022, a7 / t = 0,028, a8 / t = 0,0046, a9 / t = 0,0046, a10 / t = 0,009, a11 / t = 0,0046, a12 / t = 0,009, a13 / t = 0,009, a14 / t = 0,0046.
4. В соответствии с принятым критерием оптимальности располагаем полученные отношения a i / ti в порядке возрастания. Окончательно устанавливаем следующую последовательность проверок
8® 9 ® 11 ® 14 ® 10 ® 12 ® 13 ® 2 ® 3 ® 5 ® 4 ® 6 ® 7 ® 1.
Пример 2. Основными элементами электропривода вентилятора (рис. 4.2) являются: аппарат защиты от токов короткого замыкания (1), вводное коммутационное устройство (2), силовые контакты магнитного пускателя (3), электродвигатель (4), устройство дистанционного включения и отключения электропривода (5), катушка магнитного пускателя (6).
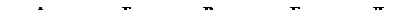
Рис. 3.2. Функциональная схема электропривода вентилятора
Буквами А, Б, В, Г, Д, Е, Ж, З обозначены входные и выходные сигналы элементов. Известны коэффициенты отказов элементов a1 = 0,3 , a2 = 0,1 , a3 = 0,1 , a4 = 0,2 , a5 = 0,1 , a6 = 0,2 . Используя метод групповых проверок, требуется составить алгоритм поиска отказавшего элемента, обеспечивающий минимальное среднее количество проверок.
Решение. 1. Составляем перечень возможных проверок (табл. 4.1). В таблицу также для каждой проверки поместим вероятности отрицательного исхода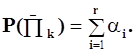 
Таблица 3.1
| Пk | Входной сигнал | Выходной сигнал | Проверяемые элементы | Р( )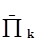
|
| П1 П2 П3 П4 П5 П6 П7 П8 П9 П10 П11 П12 П13 П14 П15 П16 П17 П18 П19 П20 | А А А А А Б Б Б Б Б ВЗ Г Е Ж Е ЕВ ЕВ ВЖ ВЖ ВЗ | Б В Г ВЖ ВЗ ВЕ ВЖ ВЗ Г Д Г Д Ж З З Г Д Г Д Д | 1 1,2 1,2,3,5,6 1,2,5 1,2,5,6 2 2,5 2,5,6 2,3,5,6 2,3,4,5,6 3 4 5 6 5,6 3,5,6 3,4,5,6 3,6 3,4,6 3,4 | 0,3 0,4 0,8 0,5 0,7 0,1 0,2 0,4 0,5 0,7 0,1 0,2 0,1 0,2 0,3 0,4 0,6 0,3 0,5 0,3 |
Из анализа последнего столбца таблицы видно, что минимальное значение критерия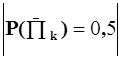 
соответствует проверкам П4, П9, П19.У проверки П9 4 элемента проверяется. Поэтому рассмотрение ведем по П4 и П19, имеющих по 3 элемента. Выбираем проверку П19 т.к. ее легче реализовать. При положительном исходе проверки П19 отказавший элемент будет находиться в группе, состоящей из 1, 2 и 5 элементов, а при отрицательном исходе – группе элементов 3, 6, 4.
2. Составляем перечни возможных проверок и вероятности их отрицательных исходов для вновь полученных групп, состоящих из 1, 2, 5 и 3, 6,4 элементов. Результаты показаны в табл. 3.2 и табл. 3.3. В этих таблицах Р(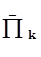 
) будет определяться суммой значений вероятностей отрицательного исхода ( для П1 : Р( 
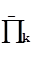) = 0,3+0,3. Первое 0,3 взято из табл. 3.1, а второе 0,3 значение вероятности элемента).
Таблица3.2
| Пk | Входной сигнал | Выходной сигнал | Проверяемые элементы | Р( )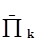
|
| П1 П2 П6 П7 | А А Б Б | Б ВЕ ВЕ ВЖ | 1 1,2 2 2,5 | 0,6 0,8 0,2 0,4 |
Таблица 3.3
| Пk | Входной сигнал | Выходной сигнал | Проверяемые элементы | Р( )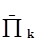
|
| П11 П12 П18 П20 | ВЗ Г ВЖ ВЗ | Г Д Г Д | 3 4 3,6 3,4 | 0,2 0,4 0,6 0,6 |
3. Проводим анализ материалов табл. 3.2 и 3.3. Данные табл. 3.2 свидетельствуют о том, что наиболее информативными являются проверки П1 и П7. Для обеих проверок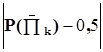 
= 0,1 . Выбираем проверку П1. При отрицательном исходе ее неисправен элемент 1, при положительном исходе – несправный элемент находится в группе элементов 2 и 5. Так как в последнем случае остается только 2 элемента, то дальнейшая последовательность проверок безразлична. Аналогичный подход применим при рассмотрении табл. 3.3.
Выбираем проверку П12 и П18. При положительном исходе проверки П12 нужно проверить элементы 3 и 6, при отрицательном – несправен элемент 4.
4. Строим алгоритм проверок
Литература
1. Ермолин Н.П., Жерихин И.П. Н Надежность электрических машин. Л.: Энергия, 1976.
2. Хорольский В.Я., Медведев А.А., Жданов В.Г. Задачник по эксплуатации электрооборудования. Ставрополь, 1997.
Приложения
Приложение 1
Функция Лапласа Ф ( х )
| Х | Ф(х) | Х | Ф(х) | Х | Ф(х) | Х | Ф(х) |
| 0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 1,00 | 0,500 0,519 0,539 0,559 0,579 0,598 0,618 0,639 0,665 0,673 0,691 0,709 0,725 0,742 0,758 0,779 0,788 0,802 0,816 0,829 0,841 | 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 1,45 1,50 1,55 1,60 1,65 1,70 1,75 1,80 1,85 1,90 1,95 2,00 2,05 | 0,853 0,864 0,874 0,885 0,894 0,903 0,911 0,919 0,926 0,933 0,939 0,945 0,950 0,955 0,959 0,964 0,968 0,971 0,974 0,977 0,979 | 2,10 2,15 2,20 2,25 2,30 2,35 2,40 2,45 2,50 2,55 2,60 2,65 2,70 2,75 2,80 2,85 2,90 2,95 3,00 3,05 3,10 | 0,982 0,984 0,986 0,987 0,989 0,990 0,991 0,992 0,993 0,994 0,995 0,996 0,997 0,997 0,9974 0,9978 0,9981 0,9984 0,999 0,999 0,999 | 3,15 3,20 3,25 3,30 3,35 3,40 3,45 3,50 3,55 3,60 3,65 3,70 3,75 3,80 3,85 3,90 3,95 4,00 4,5 5,0 6,0 | 0,999 0,9993 0,9994 0,9995 0,9996 0,9997 0,9998 1,0 1,0 1,0 1,0 1,0 1,0 1,0 1,0 1,0 1,0 1,0 1,0 1,0 1,0 |
Приложение 2
Значение гамма - функций Г(х).
| Х | Г(х) | Х | Г(х) | Х | Г(х) | Х | Г(х) |
| 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 | 1,00000 0,99433 0,98884 0,98355 0,97844 0,97350 0,96874 0,96415 0, 95973 0,95546 0,95135 0,94740 0,94359 0,93993 0,93642 0,93304 0,92980 0,92670 0,92373 0,92089 0,91817 0,91558 0,91311 0,91075 0,90852 | 1,25 1,26 1,27 1,28 1,29 1,30 1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 | 0,90610 0,90440 0,90250 0,90072 0,89904 0,89747 0,89600 0,89464 0,89338 0,89222 0,89115 0,89018 0,88931 0,88854 0,88785 0,88726 0,88676 0,88636 0,88604 0,88581 0,88566 0,88560 0,88563 0,88575 0,88595 | 1,50 1,51 1,52 1,53 1,54 1,55 1,56 1,57 1,58 1,59 1,60 1,61 1,62 1,63 1,64 1,65 1,66 1,67 1,68 1,69 1,70 1,71 1,72 1,73 1,74 | 0,88623 0,88659 0,88704 0,88757 0,88818 0,88887 0,88964 0,89049 0,89142 0,89243 0,89352 0,89468 0,89592 0,89724 0,89864 0,90012 0,90167 0,90330 0,90500 0,90678 0,90864 0,91057 0,91258 0,91467 0,91683 | 1,75 1,76 1,77 1,78 1,79 1,80 1,81 1,82 1,823 1,84 1,85 1,86 1,87 1,88 1,89 1,90 1,91 1,92 1,93 1,94 1,95 1,96 1,97 1,98 1,99 2,00 | 0,91906 0,92137 0,92376 0,92623 0,92877 0,93138 0,93408 0,93685 0,93369 0,94261 0,94561 0,94869 0,95184 0,95507 0,95838 0,96177 0,96523 0,96877 0,97240 0,97610 0,97988 0,98374 0,98768 0,99171 0,99581 1,00000 |
Приложение 3
Значение функции распределения Пуассона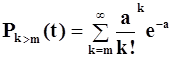 
| a | ||||||||||
| m | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| 0 | 1,000 | 000 | 000 | 000 | 000 | 000 | 000 | 000 | 000 | 000 |
| 1 | 0,095 | 1813 | 2592 | 3297 | 3935 | 4512 | 5034 | 5507 | 5934 | 6321 |
| 2 | 0047 | 0175 | 0369 | 0616 | 0902 | 1219 | 1558 | 1912 | 2275 | 2642 |
| 3 | 0002 | 0011 | 0036 | 0079 | 0144 | 0231 | 0341 | 0474 | 0629 | 0803 |
| 4 | 0001 | 0003 | 0008 | 0018 | 0034 | 0058 | 0091 | 0135 | 0190 | |
| 5 | 0001 | 0002 | 0004 | 0008 | 0014 | 0023 | 0037 | |||
| 6 | 0001 | 0002 | 0003 | 0006 | ||||||
| 7 | 0001 | |||||||||
| m | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 |
| 0 | 1,000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
| 1 | 0,667 | 6988 | 7275 | 7534 | 7769 | 7981 | 8173 | 8347 | 8504 | 8647 |
| 2 | 3010 | 3374 | 3732 | 4082 | 4422 | 4751 | 5068 | 5372 | 5663 | 5940 |
| 3 | 0996 | 1205 | 1429 | 1665 | 1912 | 2166 | 2428 | 2694 | 2963 | 3233 |
| 4 | 0257 | 0338 | 0431 | 0537 | 0656 | 0788 | 0932 | 1087 | 1253 | 1429 |
| 5 | 0054 | 0077 | 0107 | 0143 | 0186 | 0237 | 0296 | 0364 | 0441 | 0527 |
| 6 | 0010 | 0015 | 0022 | 0032 | 0045 | 0060 | 0080 | 0104 | 0132 | 0165 |
| 7 | 0001 | 0003 | 0004 | 0006 | 0009 | 0013 | 0019 | 0026 | 0034 | 0045 |
| 8 | 0001 | 0001 | 0002 | 0003 | 0004 | 0006 | 0008 | 0011 | ||
| 9 | 0001 | 0001 | 0002 | 0002 | ||||||
| m | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 |
| 0 | 1,000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
| 1 | 0,87 | 8892 | 8997 | 9093 | 9179 | 9257 | 9328 | 9392 | 9450 | 9502 |
| 2 | 6204 | 6454 | 6691 | 6916 | 7127 | 7326 | 7513 | 7689 | 7854 | 8009 |
| 3 | 3504 | 3773 | 4040 | 4303 | 4562 | 4816 | 5064 | 5305 | 5540 | 5768 |
| 4 | 1514 | 1806 | 2007 | 2213 | 2424 | 2640 | 2859 | 3081 | 3304 | 3528 |
| 5 | 0621 | 0725 | 0838 | 0959 | 1088 | 1226 | 1371 | 1523 | 1682 | 1847 |
| 6 | 0204 | 0249 | 0300 | 0357 | 0420 | 0490 | 0567 | 0651 | 0742 | 0839 |
| 7 | 0059 | 0075 | 0094 | 0116 | 0142 | 0172 | 0206 | 0244 | 0287 | 0335 |
| 8 | 0015 | 0020 | 0026 | 0033 | 0042 | 0053 | 0066 | 0081 | 0099 | 0119 |
| 9 | 0003 | 0005 | 0006 | 0009 | 0011 | 0015 | 0019 | 0024 | 0031 | 0038 |
| 10 | 0001 | 0001 | 0001 | 0002 | 0003 | 0004 | 0005 | 0007 | 0009 | 0011 |
| 11 | 0001 | 0001 | 0001 | 0002 | 0002 | 0003 | ||||
| 12 | 0001 | 0001 | ||||||||
| m | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3.8 | 3,9 | 4,0 |
| 0 | 1,000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
| 1 | 0,995 | 9592 | 9631 | 9666 | 9698 | 9727 | 9753 | 9776 | 9798 | 9817 |
| 2 | 8153 | 8288 | 8414 | 8532 | 8641 | 8743 | 8838 | 8926 | 9008 | 9084 |
| 3 | 5988 | 6201 | 6406 | 6603 | 6792 | 6973 | 7146 | 7311 | 7469 | 7619 |
| 4 | 3752 | 3975 | 4197 | 4416 | 4634 | 4848 | 5058 | 5265 | 5468 | 5665 |
| 5 | 2018 | 2194 | 2374 | 2558 | 2746 | 2936 | 3128 | 3322 | 3516 | 3712 |
| 6 | 0943 | 1054 | 1171 | 1295 | 1424 | 1559 | 1699 | 1844 | 1994 | 2149 |
| 7 | 0388 | 0446 | 0510 | 0579 | 0653 | 0733 | 0818 | 0909 | 1005 | 1107 |
| 8 | 0142 | 0168 | 0198 | 0231 | 0267 | 0308 | 0352 | 0401 | 0454 | 0511 |
| 9 | 0047 | 0057 | 0069 | 0083 | 0099 | 0117 | 0137 | 0160 | 0185 | 0214 |
| 10 | 0014 | 0018 | 0022 | 0027 | 0033 | 0040 | 0048 | 0058 | 0069 | 0081 |
| 11 | 0004 | 0005 | 0006 | 0008 | 0010 | 0013 | 0016 | 0019 | 0023 | 0028 |
| 12 | 0001 | 0001 | 0002 | 0002 | 0003 | 0004 | 0005 | 0006 | 0007 | 0009 |
| 13 | 0001 | 0001 | 0001 | 0001 | 0002 | 0002 | 0003 | |||
| 14 | 0001 | 0001 | ||||||||
| m | 4,1 | 4,2 | 4,3 | 4,4 | 4,5 | 4,6 | 4,7 | 4.8 | 4,9 | 5,0 |
| 0 | 1,000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
| 1 | 0,983 | 9850 | 9864 | 9877 | 9889 | 9899 | 9909 | 9918 | 9926 | 9933 |
| 2 | 9155 | 9220 | 9281 | 9337 | 9389 | 9437 | 9482 | 9523 | 9561 | 9596 |
| 3 | 7762 | 7898 | 8026 | 8149 | 8264 | 8374 | 8477 | 8575 | 8667 | 8753 |
| 4 | 5858 | 6046 | 6228 | 6406 | 6577 | 6743 | 6903 | 7058 | 7207 | 7350 |
| 5 | 3907 | 4102 | 4296 | 4488 | 4679 | 4868 | 5054 | 5237 | 5418 | 5595 |
| 6 | 2307 | 2469 | 2633 | 2801 | 2971 | 3142 | 3316 | 3490 | 3665 | 3840 |
| 7 | 1214 | 1325 | 1442 | 1564 | 1689 | 1820 | 1954 | 2092 | 2233 | 2378 |
| 8 | 0573 | 0639 | 0710 | 0786 | 0866 | 0951 | 1040 | 1133 | 1231 | 1334 |
| 9 | 0245 | 0279 | 0317 | 0358 | 0403 | 0451 | 0503 | 0558 | 0618 | 0681 |
| 10 | 0095 | 0111 | 0129 | 0149 | 0171 | 0195 | 0222 | 0251 | 0283 | 0318 |
| 11 | 0034 | 0041 | 0048 | 0057 | 0067 | 0078 | 0090 | 0104 | 0120 | 0137 |
| 12 | 0011 | 0014 | 0017 | 0020 | 0024 | 0029 | 0034 | 0040 | 0047 | 0055 |
| 13 | 0003 | 0004 | 0005 | 0007 | 0008 | 0010 | 0012 | 0014 | 0017 | 0020 |
| 14 | 0001 | 0001 | 0002 | 0002 | 0003 | 0003 | 0004 | 0005 | 0006 | 0007 |
| 15 | 0001 | 0001 | 0001 | 0001 | 0001 | 0002 | 0002 | |||
| 16 | 0001 | 0001 | ||||||||
Приложение 4
Продолжительность простоя технологических процессов
| Предприятия | Технологический процесс | Допустимое время простоя, ч |
| Молочные По откорму крупного рогатого скота Свиноводческие (откорм свиней) Приготовление кормов Закрытого грунта | Доение Поение Кормление Обеспечение требуемого микроклимата Первичная обработка молока Удаление навоза Поение Кормление Обеспечение требуемого микроклимата Удаление навоза Поение Кормление Обеспечение требуемого микроклимата при температуре наружного воздуха,С: 0 ...+12 +13...+20 -20...-1 Удаление навоза Приготовление витаминной муки Обеспечени микроклимата при температуре наружного воздуха,С: -35...-20 -15...-5 0 | 1,5 3,0 3,0 3,5 3,0 8,0 3,0 3,5 3,5 8,0 3,0 4,0 6,0 3,0 - 8,0 3,5 4/7* 7/12 9/- |
*В числителе приведены данные при выращивании огурцов и томатов, в знаменателе - зелени.
Приложение 5
Определение среднего числа простаивающих технологических процессов
| a | ||||||
| n | m | 2*10-2 | 1*10-2 | 8*10-3 | 6*10-3 | 4*10-3 |
| nп | nп | nп | nп | nп | ||
| 6 | 0 | 0,129 | 0,062 | 0,049 | 0,036 | 0,024 |
| 1 | 0,016 | 0,0037 | 0,0023 | 0,0013 | 0,0006 | |
| 10 | 0 | 0,236 | 0,108 | 0,085 | 0,062 | 0,041 |
| 1 | 0,047 | 0,0108 | 0,085 | 0,062 | 0,041 | |
| 2 | 0,0094 | 0,001 | 0,0005 | 0,0002 | 0,0001 | |
| 14 | 0 | 0,362 | 0,158 | 0,123 | 0,09 | 0,059 |
| 1 | 0,101 | 0,022 | 0,014 | 0,0075 | 0,0032 | |
| 2 | 0,028 | 0,003 | 0,0015 | 0,0006 | 0,0002 | |
| 3 | 0,0007 | 0,0004 | 0,0002 | 0,0001 | 0 | |
| 20 | 0 | 0,605 | 0,242 | 0,186 | 0,134 | 0,086 |
| 1 | 0,239 | 0,048 | 0,029 | 0,016 | 0,0069 | |
| 2 | 0,095 | 0,0097 | 0,0047 | 0,0019 | 0,0006 | |
| 3 | 0,038 | 0,0019 | 0,0008 | 0,0002 | 0 | |
| 4 | 0,015 | 0,0004 | 0,0001 | 0 | 0 | |
| 5 | 0,006 | 0,0001 | 0 | 0 | 0 |
Приложение 6
Таблица значений функции е-х.
|
|
| Доли х |
| ||||||
| х | 0 | 0 ,001 | 0,002 | 0,003 | 0,004 | ||||
| 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 | 1,0000 0,9900 0,9802 0,9704 0,9608 0,9512 0,9418 0,9324 0,9231 0,9139 | 0,9990 0,9891 0,9792 0,9695 0,9598 0,9502 0,9408 0,9315 0,9222 0,9130 | 0,9980 0,9881 0,9782 0,9685 0,9588 0,9493 0,9399 0,9305 0,9213 0,9121 | 0,9970 0,9871 0,9773 0,9675 0,9579 0,9484 0,9389 0,9226 0,9204 0,9112 | 0,9960 0,9861 0,9763 0,9666 0,9570 0,9474 0,9380 0,9287 0,9194 0,9103 | ||||
|
|
| Доли х |
| ||||||
| х | 0,005 | 0 ,006 | 0,007 | 0,008 | 0,009 | ||||
| 0,00 | 0,9950 | 0,9940 | 0,9930 | 0,9920 | 0,9910 | ||||
| 0,01 | 0,9851 | 0,9841 | 0,9831 | 0,9822 | 0,9812 | ||||
| 0,02 | 0,9753 | 0,9743 | 0,9734 | 0,9724 | 0,9714 | ||||
| 0,03 | 0,9656 | 0,9646 | 0,9637 | 0,9627 | 0,9618 | ||||
| 0,04 | 0,9560 | 0,9550 | 0,9541 | 0,9531 | 0,9522 | ||||
| 0,05 | 0,9465 | 0,9455 | 0,9446 | 0,9436 | 0,9427 | ||||
| 0,06 0,07 0,08 0,09 | 0,9371 0,9277 0,9185 0,9094 | 0,9361 0,9258 0,9176 0,9085 | 0,9352 0,9259 0,9167 0,9076 | 0,9343 0,9250 0,9158 0,9066 | 0,9333 0,9240 0,9148 0,9057 | ||||
|
|
| Доли х |
| ||||||
| х | 0 | 0 ,01 | 0,02 | 0,03 | 0,04 | ||||
| 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 18, 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 | 0,9048 0,8187 0,7408 0,6703 0,6065 0,5484 0,4966 0,4493 0,4066 0,3679 0,3329 0,3012 0,2725 0,2466 0,2231 0,2019 0,1827 0,1653 0,1496 0,1353 0,1225 0,1108 0,1003 0,0907 0,0821 0,0743 0,0672 0,0608 0,0550 | 0,8959 0,8106 0,7334 0,6637 0,6005 0,5434 0,4916 0,4449 0,4025 0,3642 0,3296 0,2982 0,2698 0,2441 0,2209 0,1999 0,1809 0,1637 0,1481 0,1340 0,1212 0,1097 0,0993 0,0898 0,0813 0,735 0,0665 0,0602 0,0545 | 0,8869 0,8025 0,7261 0,6570 0,5945 0,5379 0,4868 0,4404 0,3985 0,3606 0,3263 0,2952 0,2671 0,2417 0,2187 0,1979 0,1791 0,1620 0,1466 0,1327 0,1200 0,1086 0,0983 0,0889 0,0805 0,0728 0,0659 0,0596 0,0539 | 0,8781 0,7945 0,7189 0,6505 0,5886 0,5326 0,4819 0,4360 0,3946 0,3570 0,3230 0,2923 0,2645 0,2393 0,2165 0,1959 0,1773 0,1604 0,1451 0,1313 0,1188 0,1075 0,0973 0,0880 0,0797 0,0721 0,0652 0,0590 0,0534 | 0,8694 0,7866 0,7118 0,6440 0,5825 0,5273 0,4771 0,4317 0,3906 0,3535 0,3198 0,2894 0,2618 0,2369 0,2144 0,1940 0,1755 0,1588 0,1437 0,1300 0,1177 0,1065 0,0963 0,0872 0,0789 0,0714 0,0646 0,0584 0,0529 | ||||
|
|
| Доли х |
| ||||||
| х | 0,05 | 0 ,06 | 0,07 | 0,08 | 0,09 | ||||
| 0,1 | 0,8607 | 0,8521 | 0,8437 | 0,8353 | 0,8270 | ||||
| 0,2 | 0,7788 | 0,7711 | 0,7634 | 0,7558 | 0,7483 | ||||
| 0,3 | 0,7047 | 0,6977 | 0,6907 | 0,6839 | 0,6771 | ||||
| 0,4 | 0,6376 | 0,6313 | 0,6250 | 0,6188 | 0,6126 | ||||
| 0,5 | 0,5769 | 0,5712 | 0,5665 | 0,5599 | 0,5543 | ||||
| 0,6 | 0,5220 | 0,5169 | 0,5117 | 0,5066 | 0,5016 | ||||
| 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 | 0,4724 0,4274 0,3867 0,3499 0,3166 0,2865 0,2592 0,2346 0,2122 0,1920 0,1738 0,1572 0,1423 0,1287 0,1165 0,1054 0,0954 0,0863 0,0781 0,0707 0,0639 0,0578 0,0523 | 0,4677 0,4232 0,3829 0,3465 0,3135 0,2837 0,2567 0,2322 0,2101 0,1901 0,1720 0,1557 0,1409 0,1275 0,1153 0,1044 0,0944 0,0854 0,0773 0,0699 0,0633 0,0573 0,0518 | 0,4630 0,4190 0,3791 0,3430 0,3104 0,2808 0,2541 0,2299 0,2080 0,1882 0,1703 0,1541 0,1395 0,1262 0,1142 0,1033 0,0935 0,0846 0,0765 0,0693 0,0627 0,0567 0,0513 | 0,4584 0,4118 0,3753 0,3396 0,3073 0,2780 0,2516 0,2276 0,2060 0,1864 0,1686 0,1526 0,1381 0,1249 0,1130 0,1023 0,0926 0,0837 0,0758 0,0686 0,0620 0,0561 0,0508 | 0,4538 0,4107 0,3716 0,3362 0,3042 0,2753 0,2491 0,2254 0,2039 0,1845 0,1670 0,1511 0,1367 0,1237 0,1119 0,1013 0,0916 0,0829 0,0750 0,0679 0,0614 0,0556 0,0503 | ||||
|
|
| Доли х | |||||||
| х | 0 | 0 ,1 | 0,2 | 0,3 | 0,4 | ||||
| 3 4 5 6 | 0,0498 0,0183 0,0067 0,0025 | 0,0450 0,0166 0,0061 0,0022 | 0,0408 0,0150 0,0055 0,0020 | 0,0368 0,0136 0,0050 0,0018 | 0,0334 0,0123 0,0045 0,0017 | ||||
|
|
| Доли х |
| ||||||
| х | 0,5 | 0 ,6 | 0,7 | 0,8 | 0,9 | ||||
| 3 4 5 6 | 0,0302 0,0111 0,0041 0,0015 | 0,0273 0,0101 0,0037 0,0014 | 0, 0247 0,0091 0,0033 0,0012 | 0,0224 0,0082 0,0030 0,0011 | 0,0200 0,0074 0,0027 0,001 | ||||
Приложение 7
Интенсивность отказов электротехнических изделий.
| Тип элемента | Интенсивность отказов, 10-6 ч-1 |
| Транзисторы Диоды Резисторы Конденсаторы Контактные соединения Интегральные микросхемы Катушки индуктивности Реле разные Переключатели Реостаты Контакторы Плавкие предохранители Лампы накаливания Нагревательные элементы Электрические счетчики Измерительные приборы Электродвигатели серии 4А Генераторы переменного тока Трансформаторы 6(10) кВ Воздушные ЛЭП до 35кВ Аккумуляторы Машины постоянного тока Электродвигатели с кольцами | 0,01 0,06 0,001 0,006 0,001 0,006 1 0,1 0,1 11,3 2,5 0,045 7,8 7,6 1,3 0,034 11 16 2,2 5,7 7,2 29 13 |
Дата: 2019-12-22, просмотров: 282.
