Решение ряда задач эксплуатационного характера по оперативному обслуживанию электрооборудования, снабжению ЭТС запасными частями, работе участков по ремонту электрооборудования и в других случаях удобно выполнять с использованием теории массового обслуживания.

Под системой массового обслуживания (СМО) будем понимать любую систему, предназначенную для обслуживания потока требований. Ограничимся рассмотрением пуассоновских СМО с простейшим потоком требований.

Работа СМО определяется следующими параметрами:

числом каналов n,

плотностью потока заявок l,

плотностью потока обслуживания одного канала m,

числом состояний системы k.

При этом m = 1/Т_о , (2.1)

где Т_о - среднее время обслуживания одной заявки.

Системы массового обслуживания делятся на системы с отказами и системы ожиданием. В системах с отказами заявка, поступающая в момент, когда все каналы обслуживания заняты, немедленно получает отказ, покидает систему и в дальнейшем обслуживании не участвует. В системе с ожиданием заявка, заставшая все каналы занятыми, не покидает систему, а становится в очередь и ждет, пока не освободится какой-либо канал.

СМО с отказами

Вероятность состояния СМО с отказами определяется по формуле Эрланга

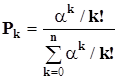
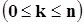, (2.2)

где 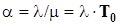 - приведенная плотность потока заявок.

Вероятность отказа (вероятность того, что поступившая заявка найдет се каналы занятыми)

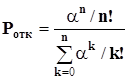
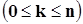 (2.3)

Для одноканальной системы

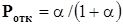 (2.4)

СМО с ожиданием

В практике работы эксплуатационных служб такие системы встречаются наиболее часто. Для СМО с ожиданием обычно определяют вероятности состояний, среднюю длину очереди, среднее время пребывания в очереди.

Вероятности состояний СМО с ожиданием при установившемся режиме работы рассчитывают по формуле

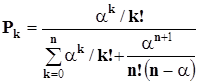
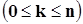 (2.5)

Вероятность наличия очереди

R_o = 1-(P₀+P₁+P₂+ … + P_n) (2.6)

Средняя длина очереди

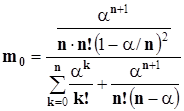 (2.7)

Среднее время пребывания в очереди

t₀ = m₀/ l (2.8)

2.2 Аналитический метод расчета резервного фонда электрооборудования

В практике решения задач о количестве запасных элементов для технических систем широкое распространение получил упрощенный аналитический метод.

При экспоненциальном законе распределения длительности безотказной работы и простейшем потоке отказов вероятность того, что имеющихся в хозяйстве запасных элементов хватит для обеспечения надежной работы системы в течение времени t , определяется по формуле

Р _{k < m} ( t )= 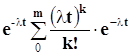, (2.9)

а вероятность того, что число отказов за время t будет больше числа резервных элементов

Р _{k > m} ( t ) = 1- Р _{k < m} ( t ) (2.10)

Значение функции распределения Пуассона Р _{k > m} ( t ) для различных значений l t и m приведены в табл. 3 приложения.

Поскольку процесс отказов электрооборудования носит случайный характер, достаточность имеющегося резервного фонда для обеспечения надежной работы электроприемников задается с определенной вероятностью. Обычно достаточность резервного фонда Р_д находится в диапазоне 0,9...0,99. Расчет необходимого запаса резервных элементов для неремонтируемого и ремонтируемого электрооборудования выполняется в следующей последовательности.