Неремонтируемые объекты работают до первого отказа. Различные показатели надежности таких объектов являются характеристиками случайной величины наработки до первого отказа. Для таких объектов обычно используются следующие показатели: P(t) - вероятность безотказной работы, f(t) - плотность распределения наработки до отказа, l (t) - интенсивность отказов, Т1 - наработка до отказа.
Вероятность безотказной работы - вероятность того, что в пределах заданного интервала времени или наработки не возникнет отказ объекта. Это убывающая функция, при t ® Ґ P(t) ® 0, значения ее находятся в диапазоне 0...1 [1].
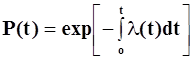= e - l t (1.1)
Плотностью распределения наработки до отказа (частотой отказов) называется производная от функции надежности [1]
a(t) = f ( t ) = dQ (t) / dt = - dP (t) / dt (1.2.)
Интенсивность отказов характеризует условную вероятность того, что объект откажет на интервале (t +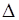 
t), при условии, что он был работоспособен в начале интервала. Интенсивность отказов определяется по формуле [1]
l ( t ) = f ( t ) / P ( t ) (1.3.)
Наработкой до первого отказа называется математическое ожидание наработки объекта до первого отказа. На основании известного соотношения между математическим ожиданием и дифференциальным законом распределения случайной величины устанавливается связь Т1 с вероятностью безотказной работы [1]
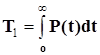(1.4)
Различные периоды работы технических устройств [1].
При рассмотрении работоспособности любого технического устройства или изделия различают три периода его “жизни”:
а) период приработки. В это время проявляются конструктивные и технологические отказы внезапного характера. Постепенные отказы практически отсутствуют. За счет устранения дефектных элементов и мест некачественной сборки и по мере приработки деталей интенсивность отказов уменьшается и в конце периода снижается до некоторого наименьшего значения. Графически это выглядит следующим образом:
l в
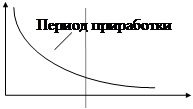
t 1 t
Рис. 1 Изменение интенсивности внезапных отказов в период приработки (участка 0-t1) примерно описывается законом Вейбулла.
б) Период нормальной эксплуатации
На этом интервале внезапные конструктивно-технологические отказы продолжают уменьшаться, но одновременно возрастает доля постепенных отказов.
l п
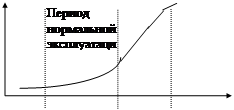
0 t 1 t 2 t 3
Рис.2. Изменение интенсивности постепенных отказов в период нормальной эксплуатации (участок t1-t2).
Участок нормальной эксплуатации обычно в десятки раз продолжительнее периода приработки. На этом участке показатели надежности достаточно строго описываются экспоненциальным распределением случайных величин.
в) Период износа
В это время преобладают постепенные отказы из-за износа и старения
электрооборудования. Интенсивность отказов постепенно растет, причем темпы роста трудно прогнозировать. На рис. 2 это характеризуется участком t2-t3. Для описания показателей надежности в большей мере подходят закономерности нормального распределения случайных величин. Суммарный же график “жизни” устройства будет иметь вид:
 |
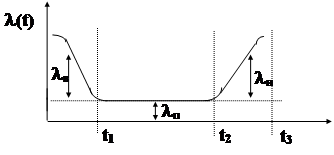Рис. 3 График “жизни” устройства l п - постепенные отказы; l в - внезапные отказы; l и - износовые отказы
Описанная закономерность появления отказов позволяет сделать следующие выводы по организации рациональной эксплуатации электрооборудования - в период приработки электрооборудования необходим более тщательный надзор за каждым элементом и постоянный контроль за режимом работы; в период нормальной эксплуатации нельзя нарушать периодичность обслуживания электрооборудования, т.к. это увеличит интенсивность отказов и преждевременно наступит период износа; в начальный период износа электрооборудование должно быть направлено в капитальный ремонт или снято с эксплуатации. Из трех рассмотренных законов распределения случайной величины наиболее часто используется показательное распределение. Оно применимо для сложных систем, характеризует работу изделия на участке длительной эксплуатации, расчеты ведутся по простым формулам. При оценке надежности используются также нормальный закон распределения на участке ускоренного износа изделий и распределение Вейбулла на участке приработки.
Для описания дискретных случайный величин в теории надежности применяется распределение Пуассона. Согласно закону Пуассона вероятность того, что случайная величина примет вполне определенное значение k, вычисляется по формуле [2]
Pk = (ak / k ! ) e-a , (1.5)
где а - параметр распределения.
Тип распределения случайной величины наработки до отказа зависит от особенностей процесса развития отказа. Для электротехнических изделий, находящихся в эксплуатации, наиболее часто применяются следующие законы распределения: экспоненциальный, нормальный, Вейбулла. Ниже в табл. 1.1.приведены формулы для оценки показателей надежности при различных законах распределения наработки до отказа.
Таблица 1.1.
| Тип распределения | Показатели надежности |
| Экспоненциальное | Вероятность безотказной работы P ( t ) = exp (-lt ) Плотность распределения f ( t ) = l exp ( - lt ) Интенсивность отказов l ( t ) = l Наработка до отказа Т1 = 1/ l |
| Вейбулла | Вероятность безотказной работы P ( t ) = exp ( -l0 tb ) Плотность распределения f ( t) =l0 b t(b-1) exp ( - l0 tb ) Интенсивность отказов l ( t ) =l0 b t( b-1 ) Наработка до отказа T1 =l0-1/b Г ( 1 + 1/b ) |
| Нормальное ( усеченное t > 0) | Вероятность безотказной работы
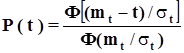Плотность распределения
Интенсивность отказов
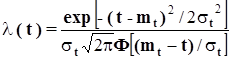Наработка до отказа
|
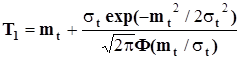
Примечание
В табл. 1.1. l0 и b - параметры распределения Вейбулла, Г - гамма - функция (см. табл. 2 приложения), mt и st - параметры нормального распределения, Ф(х) = 2/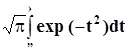 
- функция Лапласа.
1.2 Показатели безотказности ремонтируемых объектов [2]
Ремонтируемые объекты после возникновения отказа восстанавливают и продолжают эксплуатировать. Процесс их использования можно представить как последовательное чередование интервалов времени работоспособного и неработоспособного состояний. Показатели безотказности ремонтируемых объектов являются: вероятность безотказной работы Р( t ), параметр потока отказов m( t ), и средняя наработка на отказ Т.
Вероятность безотказной работы для нового оборудования рассматривается до первого отказа, а для оборудования, находящегося в эксплуатации, - до отказа после восстановления работоспособности. Расчет показателя ведется по формуле (1.1). Параметр потока отказов представляет собой отношение математического ожидания числа отказов восстанавливаемого объекта за достаточно малую наработку к величине этой наработки
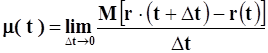, (1.6)
где D t - малый отрезок наработки; r (t) - число отказов, наступивших от начального момента времени до достижения наработки t .
Разность r (t+ D t) – r(t) представляет собой число отказов на отрезке D t.
Наработка на отказ Т характеризует среднее число часов работы между двумя соседними отказами
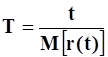, (1.7)
где t - суммарная наработка; r (t) – число отказов, наступивших в течение этой наработки; М [ r(t) ] - математическое ожидание этого числа отказов.
Дата: 2019-12-22, просмотров: 252.
