Для комплексной оценки надежности работы электрооборудования применяется коэффициент технического использования (kт и). Коэффициент технического использования – отношение математического ожидания времени работоспособного состояния объекта за некоторый период времени к суммарному времени работоспособного состояния и плановых и неплановых простоев
kт и= Т е /( Т е + ТР е + ТТО е ), (1.23)
где Т е - суммарная наработка объекта; ТР е - суммарное время простоев из-за плановых и неплановых ремонтов; ТТО е - суммарное время простоев из-за плановых и неплановых технических обслуживаний.
По сравнению с коэффициентом готовности коэффициент технического использования является более общим и универсальным показателем.
1.6 Надежность систем из последовательно и параллельно соединенных элементов [1]
Сложное техническое устройство состоит из нескольких отдельных частей или комбинации разных групп однотипных элементов. Каждая составная часть устройства обладает в течение заданного промежутка времени разным уровнем вероятности безотказной работы (или надежности). От определенного сочетания этих надежностей зависит общий уровень надежности всего устройства. Например. электрическая машина состоит из следующих основных частей: магнитопровод, обмотка статора и ротора, подшипников. Отказ любой из частей приводит к выходу из строя всей машины.
Для расчета вероятности безотказной работы машины как целого устройства в течение заданного промежутка времени нужно знать к какому типу соединения (в смысле теории надежности) принадлежит комбинация этих частей - к последовательному или параллельному.
Электрическая машина относится к устройству с последовательно соединенными элементами, т.к. выход любой из этих частей из строя приводит к отказу всей машины.
Если предположить отказы частей устройства независимыми, то на основании теорем теории вероятностей можно представить следующие уравнения для расчета надежности, например комбинации из двух частей P 1 ( t ) , P 2 ( t ) - надежность одного и другого элемента системы; Q 1 ( t ), Q 2 ( t ) - отказ одного и лругого элемента системы.
Вероятность того, что оба элемента в последовательной системе будут работать безотказно в течение заданного промежутка времени будет выглядеть так:
Рпс( t ) = P 1 ( t ) × P 2 ( t ), (1.24)
Вероятность того, что в последовательной системе один или оба элемента откажут
Q пс ( t ) = 1 - Рпс( t ), (1.25)
или Q пс ( t ) = 1- P 1 ( t ) × P 2 ( t ),
Согласно уравнению (2.1) отказ любого элемента приводит к отказу системы.
Вероятность того, что будут работать один или два элемента системы при параллельном соединении.
Рпр( t ) = P 1 ( t ) + P 2 ( t ) + P 1 ( t ) × P 2 ( t ) (1.26)
Вероятность того, что оба элемента откажут при параллельном соединении
Q пр ( t ) = Q 1 ( t ) × Q 2 ( t ) = 1- Рпр( t ) (1.27)
Параллельное соединение элементов иначе называется системой с постоянно нагруженным резервом. Такая параллельная система из двух элементов не отказывает в работе, если отказал один из элементов.
1.7 Решение типовых примеров
Пример 1. Наработка до отказа щита управления электрооборудованием подчинена экспоненциальному закону с интенсивностью отказов l ( t ) = 1,3 × 10-5 ч-1. Определить количественные характеристики надежности устройства P ( t ), f ( t ) и T 1 в течение года.
Решение. 1. По формуле P ( t ) = exp (- l t ) определяем
Р(8760) =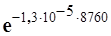 
= 0,89.
2. f(t) = l ( t ) × P(t) = 1,3 × 10 -5 × 0,89 = 1,16 × 10 -5 ч -1
3. Т1 = 1/ l = 1/(1,3 × 10 -5) = 76923 ч.
Пример 2. Сравнить между собой наработку до отказа двух неремонтируемых объектов, имеющих функцию надежности, определяемую по формулам
Р1( t ) = ехр[-(2,5× 10 -3 t)] и Р2 ( t ) = 0,7ехр - (4,1 × 10-3 t) + 0,08ехр - (0,22 × 10 -3 t).
Решение. По общей формуле для определения наработки до отказа
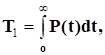
находим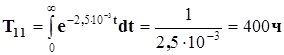 
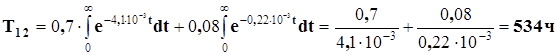
Наработка до отказа второго объекта выше, чем первого.
Пример 3. Вероятность безотказной работы машины постоянного тока на этапе приработки подчиняется распределению Вейбулла с параметрами l 0 = 2 × 10-4 ч-1 и b = 1,2. Определить вероятность безотказной работы и наработку до отказа машины за время t = 400 ч.
Решение. 1. Р( t ) = exp- (l0tb) = exp-(2 × 10-4 ×4001,2) = 0,767
2. T1 = l0-1/bГ(1+1/b) = (2 × 10-4 )-1/1,2×Г(1+1/1,2) = 1126 ч.
Значения гамма-функции взято по табл.2 приложения.
Пример 4. На испытаниях находилось N= 1000 осветительных приборов. За время t = 3000 ч отказало n = 200 изделий. За последующие Dti = 200 ч отказало еще Dni = 100 изделий. Определить Р*(3000), Р*(3200), f*(3200), l*(3200).
Решение
1. 
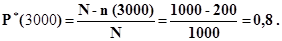
2. 
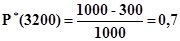
3. 
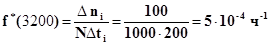
4. 
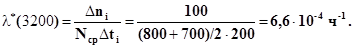
Пример 5. Прибор состоит из четырех блоков. Отказ любого из них приводит к отказу прибора. Первый блок отказал 9 раз в течение 21000 ч, второй - 7 раз в течение 16000 ч, третий - 2 раза и четвертый - 8 раз в течение 12000 ч работы. Определить наработку на отказ, если справедлив экспоненциальный закон надежности.
Решение. 1. Определяем суммарную наработку прибора
t = 21000 + 16000 + 12000 + 12000 = 61000 ч.
2. Определяем число отказов за суммарное время наработки
r ( t ) = 9 + 7 + 2 + 8 = 26
3. Находим среднюю наработку на отказ
Т* = t / r ( t ) = 61000 / 26 = 2346 ч.
Пример 6. При эксплуатации электрооборудования животноводческой фермы зарегистрировано 20 отказов, из них: электродвигателей - 8, магнитных пускателей - 2, реле - 4, электронагревательных приборов - 6. На ремонт затрачивалось: электродвигателей - 1,5 ч, магнитных пускателей - 25 мин, реле - 10 мин, электронагревателей - 20 мин. Найти среднее время восстановления.
Решение 1. Определяем вес отказавших элементов по группам mi = ni / No
m1 = 8/20 = 0,4; m2 = 2/20 = 0,1; m3 = 4/20 = 0,2; m4 = 6/20 = 0,3.
2. Находим среднее время восстановления
ТВ*=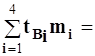 
90 × 0,4 + 25 × 0,1+10 × 0,2+20 × 0,3 = 46,5 мин
Пример 7. В результате наблюдения за работой 1000 электродвигателей в течение 10000 ч было получено значение l = 0,8×10 -4 ч -1. Закон распределения отказов экспоненциальный, среднее время ремонта электродвигателя равно 4,85 ч. Определить вероятность безотказной работы, наработку до первого отказа, коэффициент готовности и коэффициент оперативной готовности.
Решение.
1. Р ( t ) = е -l t = e - 0,8×10^-4 × 10^4 = 0,45
2. T1 = 1/l = 1250 ч.
3. kг = Т1 / (Т1 + Тв) = 1250/(1250 +4,85) = 0,996
4. kог = Р( t )kг = 0,45× 0,996 = 0,448
Пример 8. Навозоуборочный транспортер имеет 2 электродвигателя. Суммарная наработка транспортера за год составляет 200 ч. Эксплуатационные мероприятия включают в себя 1 текущий ремонт продолжительностью 3 ч на каждый электродвигатель и 7 технических обслуживаний по 0,5 ч на каждый электродвигатель. Определить коэффициент технического использования электродвигателей навозоуборочного транспортера.
Решение
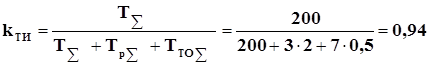
Пример 9. Тиристорный преобразователь имеет параметры усеченного нормального распределения m= 1200 ч и st = 480 ч. Определить значение вероятности безотказной работы и интенсивности отказов для t = 200 ч.
Решение
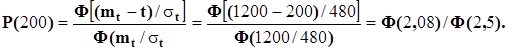
Значения Ф(2,08) и Ф(2,5) найдем по табл. 1 приложения. Тогда Р(200) = 0,982/0,993 = 0,988.
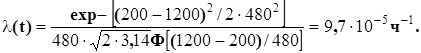
Эти зависимости пригодны для исследования электрических машин как в целом, так и поэлементно.
Пример 10. Необходимо произвести приближенную оценку вероятности безотказной работы Р(t) и среднюю наработку до первого отказа То асинхронного электродвигателя для двух промежутков времени его работы t = 1000 и 3000 ч, если интенсивность отказов l = 20 × 10 -6 ч -1.
Решение
Т1 = 1/l = 10 6 /20 = 5 × 10 4 ч.
При Р ( t ) = е -(t/10)
Р(1000) =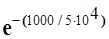 
= е - 0,02 = 0,98
Р(3000) =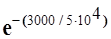 
= е - 0,06 = 0,94
Пример 11. Для системы автоматического управления известно
l = 0,01 ч -1 и время работы t = 50 ч. Определить:
Р ( t ); Q ( t ); f ( t ); T1.
Решение:
Р ( 50 ) = е -l t = е - 0,01×50 = е - 0,5 = 0,607
Q ( 50 ) = 1 - Р ( 50 ) = 1 - 0,607 = 0,393
Т1 = 1/l = 1 / 0,01 = 100 ч.
f ( 50 ) = l е -l t = 0,01× е - 0,01×50 = 0,00607 ч -1.
Пример 12. Определить конструкционную надежность электродвигателя постоянного тока для трех промежутков времени его работы: t1 = 1000 ч., t2 = 3000 ч., t3 = 5000 ч о следующим средним статистическим данным об интенсивности отказов основных её частей в долях единицы на час работы: магнитная система с обмоткой возбуждения l1 = 0,01×10-6 ч -1 ; обмоткой якоря l2 = 0,05 × 10 -6 ч -1; подшипники скольжения l3 = 0,4 ×10-6 ч -1 ; коллектор l4 = 3 ×10-6 ч -1 ; щеточное устройство l5 = 1 ×10-6 ч -1 .
Решение. Определим среднюю результирующую интенсивность отказов всех частей машины
l = l1 + l2 + l3 + l4 + l5 = (0,01+0,05+0,4+3+1)×10-6 = 4,46 ×10-6 ч -1 .
Средняя наработка до первого отказа машины
Т1 = 1/ l = 106 / 4,46 = 2,24×105 ч.
Вероятность безотказной работы или конструкционная надежность рассматриваемой машины для трех промежутков времени работы будет
Р(1000) =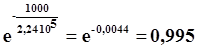 
Р(3000) = е - 0,014 = 0,988
Р(5000) = е -0,022 = 0,975
Статистическая оценка интенсивности отказов может быть определена отношением числа отказавших изделий к моменту времени D t к числу изделий поставленных на эксплуатацию (в начале испытания).
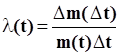
Например, испытанию подверглись 100 дверей шахты лифты и в интервале между седьмыми и восьмыми сутками испытаний было зарегистрировано 46 отказов. Тогда l = 46/100 = 0,46 отказа за сутки на дверь шахты для оговоренного интервала времени.
Пример. 13. Определить вероятность безотказной работы узла, состоящего из трех элементов, у которых вероятность безотказной работы Р1 = 0,92; Р2 = 0,95; Р3 = 0,96
Решение
Рузла(t) = Р1(t) × Р2(t) × Р3(t) = 0,92 × 0,95 × 0,96 = 0,84
Она меньше, чем вероятность безотказной работы самого надежного элемента.
Даже если взять 4 элемента и у четвертого элемента Р4 ( t ) = 0,97, то
Рузла(t) = 0,92 × 0,95 × 0,96 × 0,97 = 0,81
При последовательной системе соединения элементов лучше иметь меньше элементов в цепи
Ру = 0,92 × 0,95 = 0,874
При параллельном соединении
Рузла(t) = Р1(t) + Р2(t) - Р1(t) × Р2(t) = 0,92 + 0,95 - 0,92 × 0,95 = 1,87 - 0,874 = 0,996.
2.Определение резервного фонда электрооборудования [2]
Дата: 2019-12-22, просмотров: 227.
