1.Принимаются следующие исходные условия: поток отказов оборудования простейший, отказавшие элементы заменяются, интенсивность отказов i-го изделия li, число изделий i-го типа ni, достаточность резервного фонда Рд.
2. Определяется суммарная интенсивность отказов i-го изделия
l i S = l i ni . (2.11)
3. Зная заданное время работы системы , рассчитывается параметр распределения Пуассона а= l i S t .
4. По табл. 3 приложения для заданного значения а определяется число резервных элементов такое, чтобы 1- Р k > m ( t ) > Рд.
Ремонтируемое электрооборудование
Процесс использования и пополнения запаса для такого оборудования отличается тем, что вышедшие из строя изделия подвергаются ремонту в течение времени Тр и поступают снова в резервный фонд. Вычисление объема запасных частей в этом случае ведется следующим образом.
1. По заданной интенсивности отказов элементов и их количеству определяется суммарная интенсивность отказов.
2. С учетом времени ремонта Тр и суммарной интенсивности отказов устанавливается параметр распределения Пуассона а= l S Тр.
3. Используя табл. приложения, выбирается число резервных элементов m с таким расчетом, чтобы Р k < m ( t ) > Рд.
2.3 Решение типовых примеров
Пример 1. Система диспетчерской связи энергосистемы имеет 5 каналов. В систему поступает простейший поток заявок с плотностью l = 4 вызова в минуту. Средняя продолжительность разговора 3 минуты. Определить вероятность застать систему диспетчерской связи занятой.
Решение. 1. Определяем приведенную плотность потока заявок
a = l / m = l × То = 4 × 3 = 12
2. По формуле
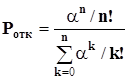
определяем Ротк = 12! / [5!(1+12/1+122/2!+123/3!+124/4!+125/5!)] = 0,63
Пример 2. Заданы параметры микропроцессорной системы: число каналов - 3, интенсивность потока обслуживания m = 20 с-1, суммарный входящий поток заявок l = 40 с-1. Определить вероятность предельного состояния и среднее время ожидания заявки в очереди. Принять СМО с неограниченной очередью.
Решение. По условию примера определяем a = l / m = 40/20 = 2, т.к. a<n, то режим системы установившийся.
Рассчитываем Рk для k=n=3
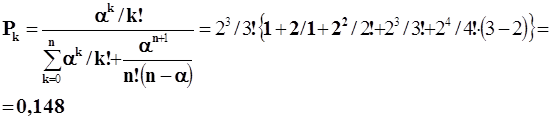
3. Для оценки среднего времени нахождения в очереди вначале определим среднюю длину очереди
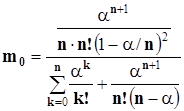
m0 = 24/{3×3!(1-2/3)2[1+2/1+22/2+23/3!+24/4!(3-2)]} = 0,9
Определяем среднее время ожидания заявки в очереди
t0 = m0 / l = 0,022 с.
Пример 3. В свинарнике - откормочнике на 3750 мест для обеспечения микроклимата используется комплект оборудования “Климат” с 20 электродвигателями серии 4А мощностью 1,1 кВт и частотой вращения 1500 мин-1. Интенсивность отказов электродвигателей l = 10 -5 ч-1, среднее время капитального ремонта отказавшего электродвигателя 30 суток. Определить резервный запас электродвигателей для свинарника, исключающий аварийный простой технологического процесса поддержания микроклимата сверх допустимой нормы tд = 3 ч. Принять kи = 0,6.
Решение. 1.Для заданного среднего времени ремонта электродвигателя Тр = 30 суток определяем
m = 1/Тр = 1/(30×24) = 1,38 × 10-3 ч-1, тогда
a = l/m = 10-5/ 1,38 × 10-3 = 0,72 × 10-2
2. Из выражения tП = nПkи/l(n- nП) c учетом того, что nП<<n определяем
nП » tПl n/ kи = 3 × 10-5 ×20/0,6 = 10-3.
3. По табл. 5 приложения для n=20, a = 0,72×10-2, nП = 10-3 устанавливаем, что в резерве необходимо иметь 4 электродвигателя. Для 4 электродвигателей среднее число простаивающих технологических процессов nП » tПln / kи = 0,0004.
4. Проверяем соответствие tд взятому приближенно tП
tП = nПkи/l(n- nП) = 0,0004× 0,6 / 10-5(20-0,0004) = 1,2 ч < tд.
Если взять 3 резервных электродвигателя, то nП= 0,0019 и
tП=nПkи/l(n- nП)= 0,0019 × 0,6 / 10-5(20-0,0019) = 5,7 ч > tд.
Таким образом, для выполнения заданных ограничений по продолжительности перерывов в работе системы микроклимата свинарника необходимо иметь 4 резервных электродвигателя.
Пример 4. На вычислительной станции сельскохозяйственного предприятия установлено 4 ЭВМ. Средняя интенсивность на выполнение расчетов - 4 заявки в час (l = 4). Среднее время решения одной задачи То = 0,5 ч. Станция принимает и ставит в очередь на решение не более 4 заявок. Заявки, поступившие на станцию, когда в очереди находится более 4 задач, получают отказ. Определить вероятность отказа и вероятность того, что все ЭВМ свободны.
Решение. 1. Имеем многоканальную СМО с ожиданием при ограниченном числе мест в очереди.
2. Предварительно вычисляем
m = 1/То = 1/0,5 = 2 ч-1, a = l/m = 2.
3. По формуле (3.3) определяем вероятность того, что все 4 ЭВМ заняты и 4 заявки стоят в очереди, тогда n=8.
Ротк = 28/[8!(1+2/1+22/2!+23/3!+24/4!+25/5!+26/6!+27/7!+28/8!)] = 0,00086.
4. По формуле (3.5) находим вероятность, что все ЭВМ свободны, k=n=4
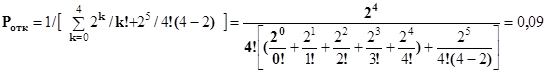
Пример 5. Требуется определить вероятность того, что отказы в системе электроснабжения появятся менее 3 раз, если параметр распределения Пуассона а = lt = 3,9.
Решение. По табл. 6 приложения определяем Рk>3(t), тогда
Рk< 3 ( t ) = 1- 0,7469 = 0,253.
Пример 6. Требуется определить число резервных электронагревательных элементов, имеющих интенсивность отказов l = 4×10-6 ч-1. Общее число электронагревательных элементов в хозяйстве 80, период пополнения резервного фонда 7000 ч. Принять достаточность резервного запаса Рд = 0,98.
Решение. 1. Определяем суммарную интенсивность отказов электронагревательных элементов lS = 4×10-6 × 80 = 3,2 × 10-4 ч-1.
2. Определяем значение параметра а
а = lS×t = 3,2 × 10-4× 7000 = 2,24
3. Для заданного значения а=2,24 по табл.6 приложения определяем Рk>m(t), равное 0,0025. Учитывая, что Р k< m ( t )= 1- Р k> m ( t )>Pд>0,98, получим
Р k< m ( t ) = 0,9925 при m = 7.
4. Поскольку Р k< 7 ( t ) = 0,9925 > Рд = 0,98, в резервном фонде целесообразно иметь 7 электронагревательных элементов.
Пример 7. В телятнике на 600 голов эксплуатируется 9 электродвигателей серии 4А, имеющих интенсивность отказов l1 = 0,1×10-4 ч-1, и 11 электродвигателей серии АО2сх с интенсивностью отказов l2 = 0,5×10-4 ч-1. Достаточность резервного фонда 0,95. Рассчитать число запасных электродвигателей при пополнении резервного фонда 1 раз в течение года ( в году 8760 часов).
Решение. 1. Определяем суммарную интенсивность отказов электродвигателей по группам
l1S= l1n1= 9 × 0,1×10-4 = 0,9×10-4 ч-1.
l2S= l2n2 = 11 × 0,5×10-4 = 5,5 ×10-4 ч-1.
2. Определяем параметры распределения Пуассона а1 и а2
а1 = l1St = 0,9×10-4×8760 = 0,788 а2 = l2St = 5,5 ×10-4×8760 = 4,82
3. По табл. 3 приложения по а1 и а2 находим значение функции Р k> m ( t ), такое чтобы Р k< m ( t ) было больше, чем Рд. Определяем число резервных элементов: для электродвигателей серии 4А :т.к. Рk < m( t ) = 1-0,0474 = 0,9526 > 0,95, то m1 = 3 ;
для электродвигателей серии АО2сх, т.к. Рk < m( t )= 1-0,025 = 0,975 > 0,95, m2 = 10.
Пример 8. 100 комплектов однотипной аппаратуры предполагается эксплуатировать в течении 500 ч. Каждый комплект аппаратуры содержит неремонтируемых элементов:
типа А n1= 5 шт c l1 = 2 ×10-6 ч-1
типа Б n2= 10 шт c l2 = 4 ×10-6 ч-1
типа С n3= 8 шт c l3 = 0,6 ×10-5 ч-1
кроме этого имеется 3 типа ремонтируемых элементов
типа Г n4= 2 шт c l4 = 1,9 ×10-5 ч-1, Тв4 = 60 ч,
типа Д n5= 10 шт c l5 = 8 ×10-6 ч-1, Тв5 = 90 ч,
типа Е n6= 3 шт c l6 = 0,4 ×10-4 ч-1, Тв6 = 42 ч.
Определить число запасных элементов по всем группам, если требуется гарантированная вероятность работы аппаратуры за счет неремонтируемых элементов каждого типа Р1 ( t ) = 0,99, а за счет ремонтируемых элементов каждого типа Р2 ( t ) = 0,96. Рассчитать также вероятность выполнения аппаратурой в целом своих функций при наличии запасных элементов.
Решение. 1. Определяем параметр а для неремонтируемых элементов (N=100).
а1 = l1Nn1t = 2 ×10-6 × 100 × 5 ×500 = 0,5
а2 = l2Nn2t = 4 ×10-6 × 100 × 10 ×500 = 2
а3 = l3Nn3t = 0,6 ×10-5 × 100 × 8 ×500 = 2,4
2. По табл. 3 приложения для полученных значений а с учетом того, что 1-Р1( t ) = 0,01 находим m1= 4, m2 = 7, m3 = 8.
3. Определяем параметр распределения Пуассона для ремонтируемых элементов
а4 = l4Nn4Тв4 = 1,9 ×10-5 × 100 × 2 × 60 = 0,228
а5 = l5Nn5Тв5 = 8 ×10-6 × 100 × 10 × 90 = 0,72
а6 = l6Nn6Тв6 = 0,4 ×10-4 × 100 × 3 × 42 = 0,5
4. По табл. 3 приложения для Р2( t ) = 0,96 находим m4 = 2, m5 = 3, m6 = 3.
5. Определяем вероятность выполнения аппаратурой своих функций
Р( t ) = 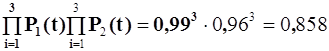
Пример 9. Решить пример 8 при условии проведения капитального ремонта вышедших из строя электродвигателей в течение 720 ч и пополнения ими резервного запаса.
Решение. 1. Определяем суммарную интенсивность отказов электродвигателей l1å=l1×n1= 9 × 0,1 × 10-4 = 0,9 × 10-4 ч-1.
l2å=l2×n2= 11 × 0,5 × 10-4 = 5,5 × 10-4 ч-1.
2. Определяем параметр а
а1= l1å ×Тр= 0,9 × 10-4 ×720 = 6,48 × 10-2
а2= l2å ×Тр= 5,5 × 10-4 ×720 = 0,396 × 10-2
Р1 k<m( t ) = 1-0,0047 = 0,9953 >0,95 (m=2)
P2 k<m ( t ) = 1-0,0079 = 0,9926 > 0,95 (m=3)
3. По табл. 3 приложения определяем число резервных элементов: для двигателей серии 4А m1 = 2, для двигателей АО2сх m 2= 3.
3. Техническая диагностика электрооборудования [2]
Дата: 2019-12-22, просмотров: 357.