Попадая в электрические и магнитные поля, заряженные частицы оказываются под действием лоренцевых сил 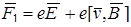 и изменяют свое первоначальное движение.
и изменяют свое первоначальное движение.
Рассмотрим движение заряженной частицы с зарядом e и скоростью v0 в однородном электростатическом поле напряженностью E. Если 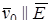 , то действующая на частицу кулоновская сила
, то действующая на частицу кулоновская сила 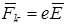 , не меняя ее направления, лишь ускоряет или замедляет ее, сообщая ей дополнительную кинетическую энергию, определяемую разностью потенциалов U:
, не меняя ее направления, лишь ускоряет или замедляет ее, сообщая ей дополнительную кинетическую энергию, определяемую разностью потенциалов U:
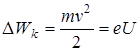 .
.

Предположим, что частица попадает в электрическое поле плоского конденсатора параллельно его пластинам. (Будем считать поле конденсатора однородным). Вдоль оси конденсатора кулоновская сила не действует, и частица сохраняет начальную скорость vx = v0. В перпендикулярном направлении под действием кулоновской силы частица приобретает ускорение 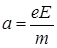 и вертикальную составляющую скорости
и вертикальную составляющую скорости 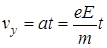 . В результате частица в конденсаторе движется по параболе: y ~ t2, x ~ t, следовательно, y ~ x2.
. В результате частица в конденсаторе движется по параболе: y ~ t2, x ~ t, следовательно, y ~ x2.
После выхода из электрического поля (из конденсатора) частица движется равномерно со скоростью v под углом α к пластинам кондесатора. Если их длина l, то время t можно найти из условия 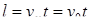 .
.
Тогда скорость v равна
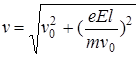 ,
,
а угол α составляет
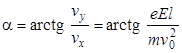 .
.

Рассмотрим теперь движение заряженной частицы с зарядом e и скоростью v0 в однородном магнитном поле индукцией B. Если частица попадает в это поле параллельно его силовым линиям ( 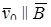 ), то действующая на частицу магнитная составляющая лоренцевой силы
), то действующая на частицу магнитная составляющая лоренцевой силы 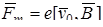 равна нулю.
равна нулю.
Если же частица влетает со скоростью v0 в магнитное поле перпендикулярно его силовым линиям, то на нее будет действовать магнитная составляющая лоренцевой силы  . Эта сила направлена перпендикулярно вектору скорости, то есть направлению движения, и является центростремительной силой. Поэтому частица будет двигаться по окружности. Следовательно, абсолютное значение скорости движения частицы v0 и ее энергия останутся постоянными при движении.
. Эта сила направлена перпендикулярно вектору скорости, то есть направлению движения, и является центростремительной силой. Поэтому частица будет двигаться по окружности. Следовательно, абсолютное значение скорости движения частицы v0 и ее энергия останутся постоянными при движении.
Радиус этой окружности определяется из условия:
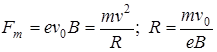 .
.
Таким образом, траектория движения частицы в перпендикулярном магнитном поле имеет радиус, обратно пропорциональный удельному заряду частицы e/m и магнитной индукции B.
Кругообразное движение заряженных частиц в магнитном поле происходит с постоянным периодом обращения, не зависящим от их скоростей:
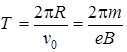 .
.
Частота обращения частицы в перпендикулярном магнитном поле называется циклотронной частотой и равна
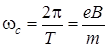 .
.
В случае, если частица влетает в однородное магнитное поле со скоростью v0 под некоторым углом α к силовым линиям, то ее скорость можно разложить на две составляющие, одна из которых vx = v0cosα параллельна полю, а другая vy = v0sinα – перпендикулярна к нему. На частицу будет действать магнитная составляющая силы Лоренца, обусловленная перпендикулярной составляющей ее скорости, то есть 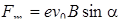 .
.
Под ее действием частица будет двигаться по окружности радиуса 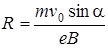 с периодом обращения
с периодом обращения
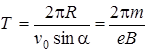 .
.

Параллельная полю составляющая скорости vx = v0cosα не вызывает появления добавочной силы, так как магнитная составляющая силы Лоренца при 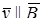 равна нулю. Поэтому в направлении поля частица двигается по инерции равномерно со скоростью vx = v0cosα. В результате сложения обоих движений частица будет двигаться по цилиндрической спирали, радиус которой приведен выше, а шаг равен
равна нулю. Поэтому в направлении поля частица двигается по инерции равномерно со скоростью vx = v0cosα. В результате сложения обоих движений частица будет двигаться по цилиндрической спирали, радиус которой приведен выше, а шаг равен
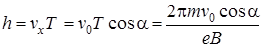 .
.
Дата: 2019-12-22, просмотров: 450.