На движущиеся заряды, кроме электростатических (кулоновских) сил действуют силы, определяемые магнитным полем – магнитные силы. Это обусловлено релятивистскими свойствами пространства-времени. Полная сила взаимодействия движущихся зарядов складывается из кулоновской силы 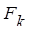 и магнитной силы 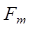, причем

.

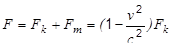Магнитная сила является величиной второго порядка малости по отношению v / c к кулоновской силе. Следовательно, магнитное взаимодействие сравнимо по величине с электростатическим лишь при больших скоростях движения зарядов.

Магнитное взаимодействие осуществляется через поле, называемое магнитным. Движущиеся заряды (токи) изменяют свойства окружающего их пространства – создают в нем магнитное поле. В отличие от электростатического, оно не действует на покоящийся заряд. Проявляется магнитное поле в том, что на движущиеся в нем заряды (токи) действуют магнитные силы.

Способность магнитного поля вызывать появление магнитной силы, действующей на какой-либо элемент тока, можно количественно описать, задавая в каждой точке поля некоторую векторную величину 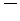, которая носит название магнитной индукции.

Тогда магнитная сила, действующая на элемент тока 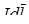, может быть представлена в виде:

.

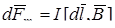(Это соотношение и определяет магнитную индукцию). Направление магнитной силы определяется направлением векторного произведения векторов элемента тока и магнитной индукции.

Магнитная индукция является основной силовой характеристикой магнитного поля.

Для магнитного поля, как и для электростатического, справедлив принцип суперпозиции: если имеется несколько токов (движущихся зарядов), то магнитная индукция результирующего поля равна векторной сумме магнитных индукций полей, содаваемых каждым из токов (движущихся зарядов):

.

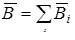Отсюда следует, что принцип суперпозиции справедлив и для элементов тока. Поэтому магнитную индукцию, создаваемую каким-либо контуром с током. можно найти, суммируя магнитные индукции от отдельных элементов тока на которые можно разбить данный контур.

Магнитные поля, создаваемые постоянными электрическими токами, подчиняются закону Био–Савара–Лапласа:

,

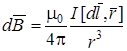где 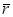 - радиус-вектор точки, в которой элемент тока  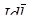создает магнитное поле индукцией .

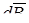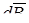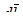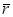Вектор магнитной индукции  направлен перпендикулярно к плоскости векторов  и , так что вращение от  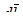к 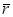 задает правым винтом его направление.

Модуль индукции магнитного поля элемента тока определяется как модуль векторного произведения:

,

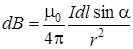где α – угол между dl и r.

Магнитное поле, обусловленное электрическими токами, является стационарным. Его нельзя осуществить движением отдельного заряда, так как в этом случае магнитное поле неизбежно будет переменным.

Единица магнитной индукции [B] = 1 Тл (тесла). Это величина магнитной индукции однородного поля, в котором на 1 м длины перпендикулярного к вектору В прямого проводника, по которому течет ток силой в 1 А, действует магнитная сила 1 Н.

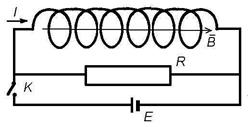
Энергия магнитного поля. Рассмотрим цепь, включающую соленоид индуктивностью L (рис.). При замкнутом ключе через соленоид протекает ток I ₀, создающий в нем магнитный поток 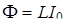. При размыкании ключа ток начинает течь через сопротивление, уменьшаясь до нуля. В результате изменяется магнитный поток и в соответствии с законом электромагнитной индукции Фарадея возникает эдс самоиндукции ε_s . Работа, которую совершит эдс самоиндукции за время своего существования,

.

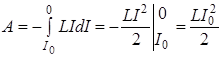Совершение этой работы сопровождается исчезновением магнитного поля, существовавшего в соленоиде. Таким образом, проводник с индуктивностью L, по которому течет ток I, обладает энергией 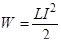, которая локализована в возбуждаемом током магнитном поле.

Выразим энергию магнитного поля через величины, характеризующие само поле. Для соленоида (заполненного однородным магнетиком с магнитной проницаемостью μ) магнитная индукция составляет 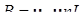 (где n – число витков на единицу длины). Тогда энергия магнитного поля

.

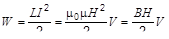Так как магнитное поле внутри бесконечного соленоида однородно и отлично от нуля только внутри него, то энергия этого поля локализована внутри соленоида и распределена по его объему с постоянной плотностью:

.

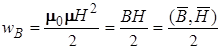Для всего пространства, в котором локализовано магнитное поле, его энергия может быть определена интегрированием по объему этого пространства

.

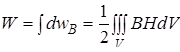22. Законы геометрической оптики. Принцип Гюйгенса – Френеля

Основу геометрической оптики образуют четыре закона: 1) закон прямолинейного распространения света; 2) закон независимости световых лучей; 3)закон отражения света; 4) закон преломления света.

1) Закон прямолинейного распространения света – в однородной среде свет распространяется прямолинейно

2) Закон независимости световых лучей – лучи при пересечении не возмущают друг друга (справедлив при небольших интенсивностях)

3) Закон отражения света:

a) падающий луч, отраженный луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча лежат в одной плоскости;

b) угол отражения равен углу падения.

4) Закон преломления света:

a) Луч падающий, преломленный и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости

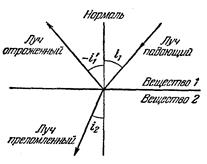
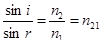
Принцип Гюйгенса – Френеля: каждая точка фронта волны является источником вторичных волн, распространяющихся во все стороны со скоростью распространения волны в среде