Взаимодействие между покоящимися зарядами осуществляется через электрическое поле. То есть, всякий заряд изменяет свойства окружающего его пространства – создает в нем электрическое поле, существующее независимо от присутствия других зарядов. Для выявления электрического поля в некоторой точке пространства нужно поместить в нее некоторый "пробный" заряд q0. По величине кулоновской силы, действующей на него, можно будет судить об интенсивности электрического поля:
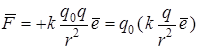 .
.
Из формулы видно, что 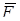 зависит от q0, однако отношение
зависит от q0, однако отношение 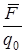 уже не зависит от величины пробного заряда и поэтому может служить характеристикой электрического поля. Эта векторная величина называется напряженностью электрического поля в данной точке:
уже не зависит от величины пробного заряда и поэтому может служить характеристикой электрического поля. Эта векторная величина называется напряженностью электрического поля в данной точке:
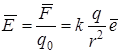 .
.
Напряженность является силовой характеристикой электрического поля и численно равна силе, действующей на единичный положительный заряд, находящийся в данной точке. Вектор 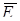 направлен от заряда, если он положителен, и к заряду, если он отрицателен. Отсюда следует, что на любой заряд q, помещенный в точку с напряженностью
направлен от заряда, если он положителен, и к заряду, если он отрицателен. Отсюда следует, что на любой заряд q, помещенный в точку с напряженностью 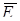 , будет действовать сила
, будет действовать сила
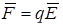
Как уже отмечалось, результирующая сила, с которой система зарядов действует на не входящий в нее заряд, равна векторной сумме отдельных сил 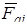 . Отсюда следует, что напряженность электрического поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый заряд в отдельности
. Отсюда следует, что напряженность электрического поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый заряд в отдельности
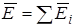 .
.
Это утверждение носит название принципа суперпозиции электрических полей. Данный принцип позволяет вычислить напряженность поля любой системы зарядов, в том числе разбив протяженные заряды на достаточно малые доли.
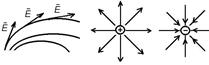
Электрическое поле можно описать, указав для каждой точки величину и направление вектора напряженности 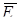 . Графически оно описывается силовыми линиями, касательная к которым в каждой точке совпадает с направлением вектора
. Графически оно описывается силовыми линиями, касательная к которым в каждой точке совпадает с направлением вектора 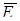 , а число линий, пронизывающих единицу перпендикулярной поверхности, численно равно E. Силовые линии нигде, кроме зарядов, не начинаются и не оканчиваются.
, а число линий, пронизывающих единицу перпендикулярной поверхности, численно равно E. Силовые линии нигде, кроме зарядов, не начинаются и не оканчиваются.
Другой – энергетической – характеристикой электрического поля является потенциал.
Работа кулоновских сил
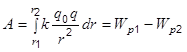 ,
,
где Wpi – потенциальная энергия заряда q0 в поле заряда q, равная
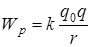 .
.
Для одной и той же точки поля отношение Wp/q0 будет одним и тем же для любой величины q0. Эта величина 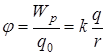 называется потенциалом электрического поля в данной точке.
называется потенциалом электрического поля в данной точке.
Потенциал численно равен работе, которую надо совершить над единичным положительным зарядом при удалении его из данной точки на бесконечность.
За единицу потенциала принимают потенциал, необходимый для перемещения заряда в 1Кл с совершением работы в 1Дж: 1 В = 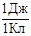 : [j]= 1 В.
: [j]= 1 В.
Связь между напряженностью электрического поля 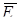 и потенциалом j можно определить следующим образом:
и потенциалом j можно определить следующим образом: 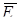 = –grad j, или
= –grad j, или 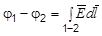 .
.
Энергия заряженного плоского конденсатора (заряды на его пластинах q и –q, а потенциалы – φ+ и φ–)
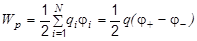 .
.
Так как q = C(φ+ – φ–) = С U, то
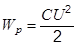 .
.
Энергия электрического поля в общем виде (после замены емкости на ее выражение
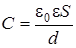 ):
):
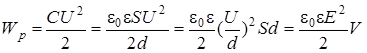 ,
,
где V – объем пространства между пластинами конденсатора, в котором сосредоточено все электрическое поле.
Если электрическое поле однородно, то плотность энергии электрического поля
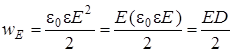 .
.
В изотропном диэлектрике (κ = const) 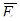 ||
|| 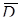 , то есть
, то есть
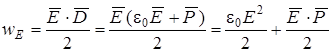 .
.
Первое слагаемое – плотность энергии электрического поля напряженностью E в вакууме, второе – плотность энергии, затрачиваемой на поляризацию вещества.
По плотности энергии электрического поля w можно найти энергию электрического поля WE, заключенную в любом объеме пространства V:
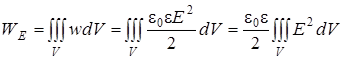 .
.
Дата: 2019-12-22, просмотров: 370.