Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

9.1. Кривые размагничивания постоянных магнитов

 

В МПТ малой мощности перспективно использование постоянных магнитов, позволяющих уменьшить габариты машин и увеличить их КПД.

Расчёт МПТ с постоянными магнитами производится теми же методами, что и машин с обмотками возбуждения. Особенностью расчёта является правильный выбор габаритов магнита при известных его параметрах.

Постоянный магнит характеризуется кривой размагничивания, снимаемой для образцов с замкнутым магнитопроводом, вид которой представлен на рис.8.

Рис. 8. Кривая размагничивания постоянного магнита

При отсутствии размагничивания режим работы магнита определяется положением точки 1 (В _r, 0) на кривой размагничивания. Значение магнитной индукции в этой точке называется остаточной индукцией В _r. Максимальная напряжённость магнитного поля, необходимая для размагничивания  магнита, называется коэрцитивной силой H_C, а режим работы магнита при  этом определён положением точки 2(0, H_C). Если постоянный магнит имеет воздушный зазор, то магнитная индукция в зазоре и самом магните оказывается меньше остаточной, т.к. его МДС распреде-

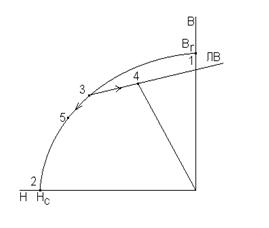
ляется между зазором и сердечником магнита. Наличие воздушного зазора эквивалентно размагничивающему действию обмотки с током. Рабочая точка постоянного магнита с зазором оказывается смещённой, занимая положение точки 3 на кривой размагничивания.

При повторном намагничивании в силу необратимых процессов, произошедших в магните, намагничивание происходит не по основной кривой, а по частному циклу (точки 3,4). Для расчётов частные циклы заменяются прямой линией, называемой линией возврата (ЛВ). Характер процессов размагничивания магнита определяется величиной МДС размагничивания. При малых значениях МДС размагничивание происходит по линии возврата до точки 3. Если же МДС значительна, то процесс размагничивания вначале происходит по линии возврата до точки 3, а затем - по основной кривой размагничивания (точка 5). Последующие режимы намагничивания в этом случае будут происходить по новой линии возврата, проходящей через точку 5.

Магнитная цепь МПТ рассчитывается так, чтобы рабочая точка лежала на середине прямой возврата, а возможные колебания МДС не выводили её за пределы данной линии возврата.

Наклон линии возврата определяется магнитной проницаемостью возврата

m_В = DВ/DН.                                              (9.1)

Значения m_В с достаточной точностью определяются наклоном касательной к кривой размагничивания в точке (В _r, 0).

Различным точкам на кривой размагничивания соответствуют различные величины удельной энергии магнита:

W_M = 0,5 B H.                                           (9.2)

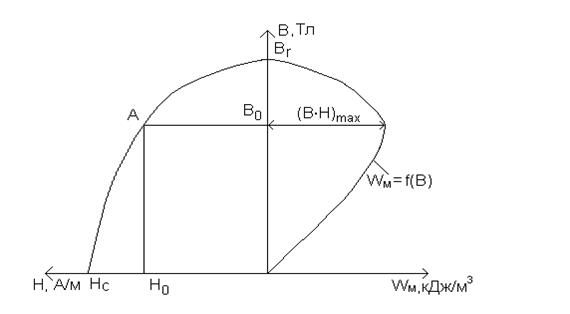
Зависимость удельной энергии от напряжённости магнита представлена на рис.9. Как видно из рисунка, при некотором значении напряжённости Н_о наблюдается максимум удельной энергии в точке А с координатами (В_о, Н_о). Магнитная система должна проектироваться так, чтобы рабочий режим магнита находился вблизи точки максимума.

Для расчётов магнитных систем с постоянными магнитами необходимо иметь аналитическое описание кривой размагничивания. Наиболее часто эта зависимость представляется в виде гиперболы:

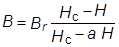.                                         (9.3)

В этом выражении коэффициент а зависит от формы кривой размагничивания и выражается через коэффициент формы g следующим образом:

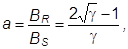                                       (9.4)

где

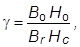                                                                                                    (9.5)

Рис.9. Удельная энергия постоянного магнита

 

В_о и Н_о - координаты точки, соответствующие максимуму энергии постоянного магнита на кривой размагничивания.

Величина коэффициента формы кривой размагничивания постоянных магнитов 0,25 £ g £ 0,9.

При g = 0,25 коэффициент а = 0 и гипербола вырождается в прямую

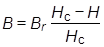,                                         (9.6)

Рис. 10. Аналитическое представление кривой размагничивания пос- тоянного магнита

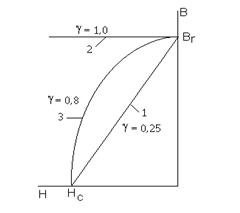
показанную на рис. 10 (кривая 1).

При g = 1 коэффициент а = 1 и уравнение гиперболы принимает вид

В = В _r,

т.е. имеем горизонтальную прямую, касательную к кривой размагничивания.

При g = 0,5 коэффициент а = 0,8 и гипербола становится близкой к окружности (кривая 3 на рис.10).

Коэффициент формы кривой размагничивания определяется материалом постоянного магнита, и для бариевых магнитов g = 0,316 -

- 0,390, для метоллокерамики g = 0,36 - 0,64, для сплавов ЮНДК g = 0,5 - 0,9, для магнитов на основе редкоземельных элементов g = 0,27 - 0,3.

 

9.2. Совместная работа постоянных магнитов

с внешней магнитной цепью

 

Простейшая магнитная цепь состоит из постоянного магнита, двух воздушных зазоров и внешнего магнитопровода.

Магнитный поток, создаваемый постоянным магнитом, состоит из основного потока, проходящего через воздушные зазоры и внешний магнитопровод, и потока рассеяния, замыкающегося по воздуху, между полюсами магнита.

Эти потоки по отношению к магниту являются внешними, и их сумма должна быть равной потоку постоянного магнита

Ф_М = Ф_ВН = Ф_d + Ф_s.                                     (9.7)

Величина потока рассеяния принимается пропорциональной МДС магнита:

                                         Ф_s = l_s F_M.                                                (9.8)

Согласно закону полного тока для магнитной цепи справедливо соотношение

2 H_M l_M + 2 H_d d + 2 H_CT l_CT = 0,                             (9.9)

где l_M и l_CT - половина длины магнита внешнего магнитопровода.

В этом случае

F_M = - (F_d + F_CT) или по модулю ½F_M½ =½F_d + F_CT½.        (9.10)

Поскольку магнитный поток пропорционален магнитной индукции, а напряжённость магнитного поля - МДС, то кривую размагничивания постоянного магнита можно изобразить в координатных осях (Ф, F). В этих же осях можно построить зависимости Ф_d = f (F_ВН) и Ф_s = f (F_м):

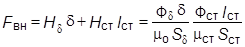.                       (9.11)

Для последовательно включенных участков Ф_СТ = Ф_d ,поэтому указанное выражение записывается в виде

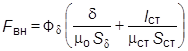,                              (9.12)

отсюда

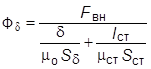.                                  (9.13)

Полученная зависимость нелинейна, так как по мере увеличения магнитной индукции материала внешнего магнитопровода его магнитная проницаемость падает (кривая Ф_d(F_ВН) на рис.11).

При выполнении условия (9.7) поток рассеяния пропорционален внешней МДС:

Ф_s = l_s F_м  = l_s F_BH,                                   (9.14)

и эта зависимость может быть построена в тех же координатных осях (кривая Ф_s (F_BH) на рис.11).

Просуммировав ординаты указанных кривых, построим ту же зависимость (9.7) с учётом нелинейности

Рис. 11. Совместная работа постоянного магнита с внешней магнитной цепью

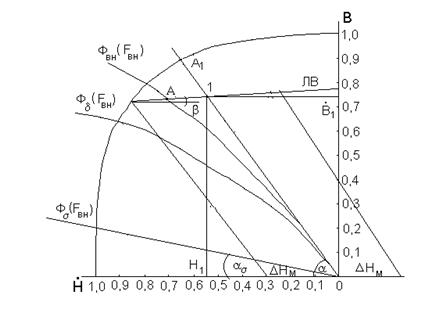
Ф_BH = Ф_d + Ф_s = f (F_BH).

 

Совместная работа постоянного магнита и внешней магнитной цепи возможна согласно (9.7) и (9.10) при равенстве магнитных потоков и МДС, т.е. в точке пересечения линии возврата магнита и вебер-амперной характеристики внешней магнитной цепи (точка А на рис.11).

В тех случаях, когда внешняя магнитная цепь не насыщена, вебер-амперная характеристика изображается прямой, проведённой относительно оси абсцисс под углом

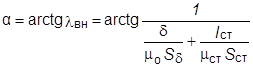,                        (9.15)

где l_ВН - магнитная проводимость внешней магнитной цепи.

Совместная работа магнита и внешней цепи соответствует рабочей точке 1 с координатами (Н₁, В₁).

Если магнитная цепь имеет обмотку, по которой протекает ток, то к МДС магнита будет добавляться МДС обмотки -DF. Эта МДС не влияет на характеристики внешней магнитной цепи. Поэтому для учёта её влияния достаточно сместить вебер-амперную характеристику внешней цепи Ф_ВН = f (F_ВН) параллельно самой себе на величину DF в зависимости от её полярности. Случай размагничивания показан на рис. 11.

Для того чтобы МДС обмотки не вызывала размагничивания постоянного магнита, необходимо ограничить её величину: DF < F_РАЗМ.

Подмагничивание магнита не вызывает ухода рабочей точки с линии возврата, и величина МДС обмотки в этом случае не ограничивается.

Таким образом, задача расчёта магнитной цепи заключается в том, чтобы, зная характеристики постоянного магнита, внешней магнитной цепи и величину размагничивающей МДС обмотки, выбрать положение рабочей точки, обеспечивающей максимум энергии, или, другими словами, минимальный объем магнита.

 

9.3. Расчёт оптимальных параметров постоянного магнита

 

Пусть задана кривая размагничивания постоянного магнита

,

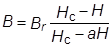с известными параметрами B _r, H_c, a.

Введём относительные величины:

,

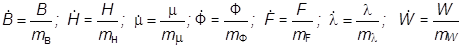где в качестве масштабов выбраны m_B = B _r; m_H = H_c; m_m = B _r / H_C; m_Ф = B _r S_M; m _F = H_C l_M; m_l = m_Ф / m _F; m _W = B _r H_C / 2.

Кривая размагничивания в относительных единицах записывается в виде

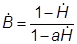.                                             (9.16)

Допустим, что рабочая точка магнита, положение которой необходимо определить, изображается на рис. 12 точкой 1. Положение этой точки, как было показано выше, соответствует точке пересечения линии возврата и вебер-амперной характеристики внешней цепи. При отсутствии насыщения наклон последней определяется выражением

tg a = l_ВН.                                               (9.17)