Состояние квантовой частицы задается волновой функцией (для одной частицы 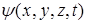 ) Состояние-это та ситуация , в данных условиях которой нах-ся система.
) Состояние-это та ситуация , в данных условиях которой нах-ся система.
Система-то множ-во взаимодей-щих эл-тов, образующих нечто целое,единое.
Волновая фун-ция – это такая функция квадрат модуля которой есть вероятность обнаружения ч-цы в том или ином месте пространства или плотности вероятности.
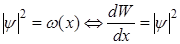
Стандартные условия: 1)непрерывность 2)ф-ция должна быть однозначная(не иметь 2 знач)
3) должна быть ограниченной (конечной)≠∞.
Условие нормировки вол.ф-ции. 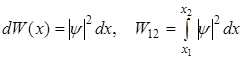 вероятность попадания час. в (x1, x2).
вероятность попадания час. в (x1, x2). 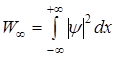 вер-сть нахождения часицы хоть где нибудь.
вер-сть нахождения часицы хоть где нибудь.
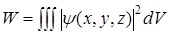 в трёх мерном пространстве.
в трёх мерном пространстве.
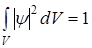 -то , что частица гдето находится , есть достоверное событие (условие нор-вки). Вер-сть достов. событ. = 1, а невоз-ного =0.
-то , что частица гдето находится , есть достоверное событие (условие нор-вки). Вер-сть достов. событ. = 1, а невоз-ного =0.
Принцип суперпозиции состояний. Если система может находится в состоянии 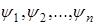
то она может находится в состоянии 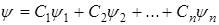 которая представляет собой произвольную линейную комбинаций состояний
которая представляет собой произвольную линейную комбинаций состояний 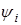 .
.
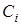 - произвольные комплексные числа.
- произвольные комплексные числа.
(В классике y1+y1=2y1 (маятник колеблется и колеблется в той же плоскости т. подвеса получаем двойное колебание с той же частотой. В квант.мех. 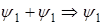 .Дело все в нормировке , приводит к тому ,что наложение двух состояний приводит к одному состоянию)
.Дело все в нормировке , приводит к тому ,что наложение двух состояний приводит к одному состоянию)
Физические величины в квантовой механике.Линейные операторы. Самосапр. операторы, их соб.фун-ции и соб.знач. Операторы координаты, импульса и мом.импульса.Коммутация операторов.Сред.знач. и вероятности возможных значений наблюдаемых.
Физ.величины кв.мех. не могут быть такими как в классической физике. В кв.мех. физич. величина характеризуется не её числовым значением, а оператором, которым она пред-ется.
В данной ситуации числовое значение физ.вел. неопределенное, а оператор в полнее определен.
Оператор- правило, по которому каждой функции из некоторого множества ф-ций сопоставляется ф-ция из тогоже мно-ва ф-ций или другого.
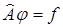
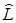 наз-ся линейным еслидля него выполняется следующее равенство
наз-ся линейным еслидля него выполняется следующее равенство
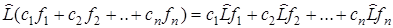
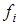 -произвольные комплексные функции
-произвольные комплексные функции
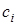 - произвольные комплексные числа
- произвольные комплексные числа
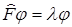 - уравнение для отыскания собственных значений и собств функций оператора
- уравнение для отыскания собственных значений и собств функций оператора 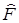 .
.
Решение ур-ния удовлетворяющее стандартным условиям наз-ся собственной функцией.
Значение 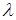 соот-щее собственным функциям наз-ся собственным значением операторов.
соот-щее собственным функциям наз-ся собственным значением операторов.
Множество соб.ф-ций – наз-ся система собственных функций.
Набор соб.значений – наз-ся спектром соб.зн-ний оператора 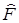 .Постулаты кв.мех.
.Постулаты кв.мех.
1)Каждой наблюдаемой отвечает определенный оператор.
2)Вол-я ф-ция сис-мы в состоянии когда физ.велич-на А принимает значение а совподает с соб-нной функ-ей оператора 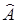 соответс-щее соб.знач-ию а.
соответс-щее соб.знач-ию а. 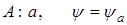
3)Если система находится в состоянии 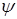 и эта функ-ция
и эта функ-ция 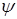 совподает с соб.функ-ей оператора некоторой физической величины, то эта виличина имеет значение совподающая с соо-щим соб.значением данного оператора.
совподает с соб.функ-ей оператора некоторой физической величины, то эта виличина имеет значение совподающая с соо-щим соб.значением данного оператора.
Операторы кв.мех. величины должны быть линейными(для выполнения принципа супер позиции) и самосапреженными(вещественность соб.значений)(Эрмитовы( 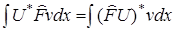 ))
))
Операторы: 1)координат 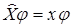 . 2)импульса
. 2)импульса 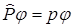
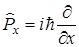
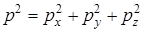
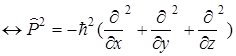
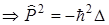
3)Оператор момента импульса 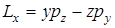 (Кл.мех)
(Кл.мех)
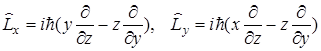
Коммутирующий оператор 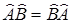 - коммутатор,
- коммутатор, 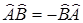 - антикомутатор.
- антикомутатор.
Сред.знач. и вероятности возможных значений наблюдаемых.
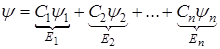
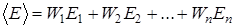
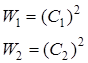
Дата: 2019-12-22, просмотров: 374.