Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Функция, предложенная Бернулли, имела вид U(x) = b*ln[(a+x)/a]. Заметно, что производная первого порядка dU(x)/dx = b/(a+x) обратно пропорциональна богатству. Кроме того,  производная второго порядка d²U(x)/dx² < 0

 

 

Приложение Д.

Модели ожидаемой полезности.

11.		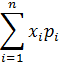Ожидаемый денежный выигрыш.
22.		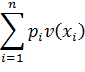Бернуллианская ожидаемая полезность. (Бернулли, 1738)
33.		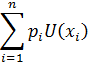Ожидаемая полезность Д. Неймана и О. Моргенштерна, (1970).
44.		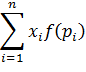Теория достоверных эквивалентов (Schneeweiss, 1974; Handa, 1977, de Finetti, 1937).
55.		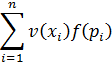Субъективная ожидаемая полезность (Edwards, 1955).
66.		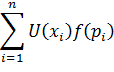Субъективная ожидаемая полезность (Ramsey, 1931; Savage, 1954; Quiggin, 1980).
77.		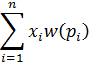Взвешенный денежный выигрыш.
88.		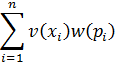Теория перспектив (Kahneman and Tversky, 1979).
99.		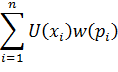Субъективная взвешенная полезность (Karmarkar, 1978).
110.		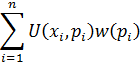Lynch, 1979; Lehner, 1980.

 

Приложение Е.

Модель неприятия риска.

 

 

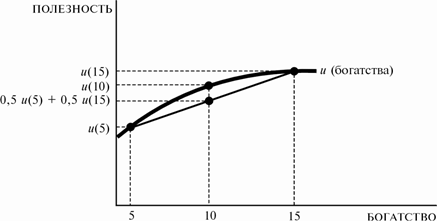
Приложение Ж.

Модель предпочтения риска.

        

 

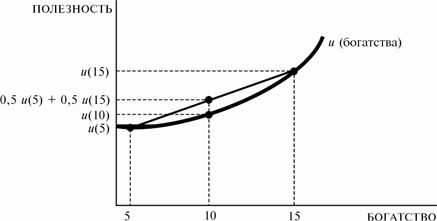
Приложение З.

Коэффициент Эрроу-Пратта.

Коэффициент Эрроу-Пратта 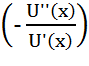 , где 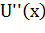 – производная U(x) второго порядка, а 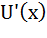- первого. Эта мера не зависит от линейных преобразований функций, и имеет постоянное значение для линейных и экспоненциальных функций полезности.

 

Приложение К.

 Риск и доход.

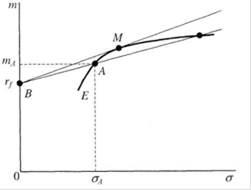
Бюджетная линия показывает издержки получения большего ожидаемого дохода, выраженные через возросшее стандартное отклонение дохода. В точке оптимального выбора кривая безразличия должна касаться бюджетной линии.

Приложение М.

Линия фондового рынка.

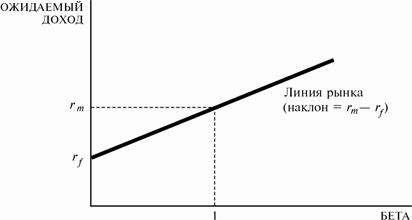
Линия рынка показывает комбинации ожидаемого дохода и беты для активов, находящихся в равновесии.

 

Приложение Н.

 Взаимные фонды.

 

 

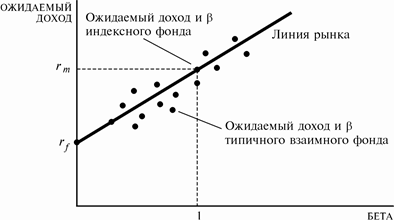
[1] Санкт-петербургский парадокс (названный так, поскольку работа Бернулли появилась в Комментариях Санкт-Петербургской Академии) заключается в следующем: монета подкидывается n раз до тех пор, пока не выпадет "орел"; затем выплачивается 2 в степени n дукатов. Парадоксально, но математическое ожидание выигрыша представляет собой бесконечно большую величину, хотя здравый смысл приводит к заключению, что справедливым вознаграждением за участие в игре должна быть ограниченная сумма.

[2] Найт Ф. Х. Риск, неопределенность и прибыль / Пер. с англ. – М.: Дело. 2003. с. 225-230.

[3] Найт Ф. Понятия риска и неопределенности // THESIS. - 1994. - Вып. 5. С. 26.

[4] В.Н. Салин, В.Г. Медведев. Понятие рисков и управления ими; методология оценки. // Вестник Финансовой академии. 2004. № 3. С. 28-41.

[5] Найт Ф.Х. «Риск, неопределенность и прибыль» / Пер. с англ. – М.: Дело, 2003. -210 с.

[6] Дж. фон Нейман, О. Моргенштерн «Теория игр и экономическое поведение». М.: Наука, 1970. – С.47.

[7] Шумейкер П. Модель ожидаемой полезности: разновидности, подходы, результаты, пределы возможностей// THESIS. – 1994. – Вып.5. – с. 32-37; Фридмен М. Анализ полезности при выборе среди альтернатив, предполагающих риск // Теория потребительского поведения и спроса. СПб. - 1993. - с. 208-249.

[8] Найт Ф.Х. «Риск, неопределенность и прибыль» / Пер. с англ. – М.: Дело, 2003. С. 230.

[9] Там же.-С. 235

[10] Нуреев Р. М. Курс микроэкономики: учебник / Р. М. Нуреев. – 2-е изд., изм. – М.: Норма, 2008. – С.400-401.

[11] Шоломицкий А.Г. Теория риска. Выбор при неопределенности и моделирование риска. -М.: ИД ГУ-ВШЭ, 2005. – С.51.