В данной главе мы постараемся рассмотреть, как влияют риски и неопределенность на рынок активов. Установим связь между доходностью актива и степенью риска.

Активы – это средства, обеспечивающие денежные поступления в форме как прямых выплат (прибыль, дивиденды, рента и т. д…), так и скрытых выплат (увеличение стоимости фирмы, недвижимости, акций и т.д…). Рисковые активы – это активы, доход от которых частично зависит от случая.[10]

Инвестор, оперирующий на финансовом рынке, где цены бумаг (например, облигаций, акций) колеблются непредсказуемым образом, вынужден принимать решения в условиях риска. Одна из наиболее известных задач в таких условиях – задача формирования инвестиционного портфеля (набора) из различных ценных бумаг. Допустим, у инвестора имеется информация о колебании цен в прошлом. Как инвестору обработать эту информацию, чтобы принять правильное решение?

Математическое ожидание (среднее значение) – наиболее простой и естественный критерий выбора в ситуациях, когда будущие поступления/потери случайны. Это также исторически самый первый критерий. Если бы инвестор действовал по правилу максимального среднего, он мог бы выбрать для инвестирования ценную бумагу с наибольшей доходностью, оцененной по данным за определенный период времени, возможно, с поправкой на будущее состояние рынка.

Такой выбор, однако, не учитывает риска возможных случайных колебаний доходностей вокруг среднего. А в условиях неопределенности это весьма важно. Поэтому широкое распространение в теории и на практике получило использование дисперсии в качестве показателя риска. Пример выбора, основанного на измерении риса дисперсии, дает так называемая модель оценки фондовых активов (capital assets pricing model – CAMP). Мы рассмотрим её лишь в самых общих чертах, преимущественно с точки зрения принципов сравнения и выбора альтернатив в условиях риска.

Теория CAMP возникла как развитие теории выбора портфеля Марковица. Марковиц ввел принцип сравнения по среднему и дисперсии, который в общем можно сформулировать так. Если рассматривать альтернативы, характеризующиеся случайными величинами, то принцип сравнения по среднему и дисперсии заключается в том, что из двух случайных величин «лучшей» считается величина, имеющая большее среднее и меньшую дисперсию.[11] Стоит отметить, что в этой формулировке скрыто подразумевающее и свойственное людям неприятие риска, а если точнее – стремление к наименьшему риску.

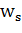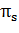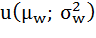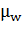В модели средней и дисперсии относительно нее предполагается, что полезность распределения вероятностей, приносящего инвестору богатство  с вероятностью , можно выразить как функцию средней данного распределения и дисперсии относительно этой средней, , где - математическое ожидание богатства, 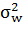- его дисперсия. Или, если это более удобно, полезность можно выразить в виде функции средней и стандартного отклонения, 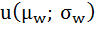, где 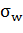- среднее квадратичное отклонение. Поскольку и дисперсия, и стандартное отклонение есть меры степени риска, характеризующей распределение вероятностей, можно считать полезность зависящей от любого из этих двух показателей.

Эту модель можно рассматривать как упрощение модели ожидаемой полезности, описанной в предыдущей главе. Если существует возможность полностью охарактеризовать варианты производимого выбора с помощью соответствующей им средней и дисперсии относительно нее, то на основе функции полезности для средней и дисперсии можно ранжировать варианты выбора таким же образом, как и на основе функции ожидаемой полезности. Но это так только в первом приближении.

Модель средняя - квадратичное отклонение применяется в простейшей задаче об оценке портфеля, содержащего различные ценные бумаги. В данной работе рассмотрим портфель, состоящий из двух ценных бумаг. Одна из них будет приносить фиксированный доход - 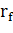. Это – безрисковый актив. Такими активами являются надежные (в основном государственные) облигации.

Другой актив - это рисковый актив. Доход по нему непостоянен во времени и зависит от многих факторов, в том числе конъюнктуры на рынке. Тогда 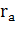 - доход на этот актив при исходе a, а  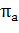- вероятность наступления данного исхода. При этом  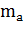- ожидаемый доход на рисковый актив, а  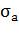- стандартное отклонение дохода.

Если обозначить через х долю средств, вложенных в рисковый актив, и соответственно (1-х) – в безрисковый актив, то ожидаемый доход на весь портфель будет задан формулой:

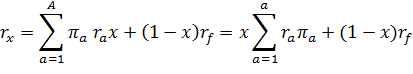
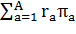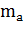= , ожидаемый доход на рисковый актив. Подставив, получим

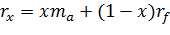
Таким образом, ожидаемый доход на портфель из двух активов есть среднее арифметическое взвешенное двух ожидаемых доходов. Если же портфель состоит из N  активов, то ожидаемый доход представится так:

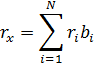
, где 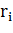- доходность одного активна,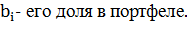

Дисперсия портфельного дохода задана формулой

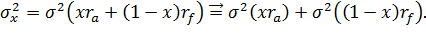
Так как 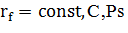дисперсия портфельного дохода будет равняться дисперсии значений рискового актива, взвешенной в ее доле.

,

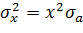
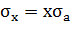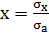
 Если подставить х в уравнение ожидаемого дохода, то получится равенство

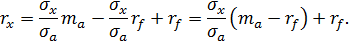
Естественно предположить, что 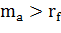, так как инвестор, не расположенный к риску, никогда не будет держать в своем портфеле рисковый актив, если он приносит более низкий ожидаемый доход, чем безрисковый актив. Отсюда следует, что если направить большую долю своего богатства на покупку рискового актива, то получится более высокий ожидаемый доход, но также при довольно большом риске. Это изображено возрастающими прямыми в приложении К.

Если выбрать x=1, то это означает, что все деньги будут вложены  в рисковый актив, ожидаемый доход и стандартное отклонение будут равняться ( 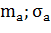). Если x=0, все инвестиции будут вложены в надежный актив и ожидаемые доход и стандартное квадратичное отклонение будут равняться ( 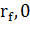). Ожидаемая доходность портфеля А, состоящего и из безрискового и из рискового активов, будет равняться
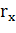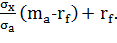 =  Причем значения доходности будут лежать на АВ, в зависимости от x.

Если на этом графике представить каждый возможный рисковый актив с определенной доходностью с помощью параметров 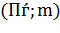, то это множество будет выпуклым вверх. Причем верхняя граница этого множества будет представлять собой границу, на которой находятся самые эффективные активы – т. е. будет соблюдаться принцип сравнения по среднему и дисперсии. В приложении К эта линия - Е – утолщена. Она называется границей эффективности.

Если отметить на границе такую точку М, что ВМ – касательная к границе эффективности, это будет означать, что ВМ – наиболее эффективная бюджетная линия. Для любой точки отрезка АВ можно указать точку отрезка ВМ, лежащую выше нее. В точке касания бюджетной линии и границы эффективности будет достигаться удовлетворение – т. е. оптимальное сочетание безрискового и рискового активов. Такое сочетание называется оптимальной комбинацией рисковых активов, а соответствующий портфель называется рыночным.

Наклон бюджетной линии называются рыночной ценой риска. То есть

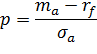
Она показывает, на сколько повышается риск портфеля на единицу прироста средней доходности.

Так что же можно сказать о применимости среднего квадратичного отклонения и среднего в качестве меры риска? Во всяком случае, это мера хорошо «работает», когда распределение случайных величии близко к нормальному. Но в свою очередь нормальное распределение в случайных экономических процессах встречается далеко не всегда. Поэтому в некоторых случаях это модель может оказаться совершенно неприемлемой. Например, дисперсия явно плохая характеристика риска для ассиметричных распределений или для распределений дискретных случайных величин.