Однако знание или тем более незнание вероятностей в рисковых ситуациях всё еще не решает проблему выбора в условиях неопределенности.

С этим кругом вопросов призвана справляться теория ожидаемой полезности. Модели ожидаемой полезности изучают выбор между рисковыми перспективами (т.е. произведениями векторов исходов 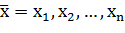 и вероятностей наступления каждого из них 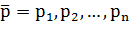.) как с одним, так и с несколькими возможными исходами. Пусть анализируется n таких исходов. Если обозначить векторы исходов через 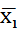, а вероятности, связанные с каждым из них, через 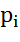,  то ожидаемая полезность в общем виде может быть определена как модель, предсказывающая или предписывающая максимизацию индивидом 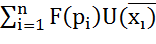.Основными особенностями модели в этой общей форме являются: 1) независимость альтернативных исходов (т.е. каждый имеет свой собственный уровень полезности); 2) независимы и преобразования вероятностей и исходов; и 3) мультипликативное сочетание вероятностей и исходов по типу вычисления ожидаемых величин после некоторых преобразований, заданных функциями F и U.

В рамках этой общей модели ожидаемой полезности существует множество разновидностей, которые различаются между собой 1) по способу измерения полезности, 2) по допустимым типам преобразования вероятностей F( 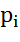), и 3) по способу измерения исходов .

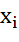Поэтому имеет смысл рассмотреть формирование моделей ожидаемой полезности с исторической точки зрения. В частности впервые об ожидаемой полезности стало известно из работ Д. Бернулли. Как уже было отмечено в начале работы, в процессе исследования т. н. Санкт-Петербургского парадокса были выдвинуты предположения о том, что индивид руководствуется оптимизацией не ожидаемого выигрыша, а ожидаемой полезности. Напомним, что суть этого парадокса заключалась в игре, в которой подбрасывалась монета до тех пор, пока не выпадет герб. Причем выигрыш будет равен 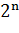ден. единиц. Если составить закон распределения случайной величины выигрыша, то значения будут такими: 2, 4, 8, 16 и т.д… ( 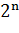), - а вероятности будут соответствовать 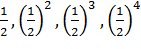и т.д… . Нетрудно подсчитать по формуле математического ожидания, что ожидаемый доход будет равняться . В ответ на это Бернули вместе с известным математиком Г. Крамером предложили, что в данной ситуации для человека важен не математический подсчет ожидания, а его субъективная оценка. Зависимость между исходами и их ценностью для индивида показывает полезность и кривые безразличия. Функция полезности, предложенная Бернулли, имеет логарифмический вид (приложение Г), тем самым показывая убывание по мере роста богатства (в данном случае выигрыша). Так же он показал, что ожидаемая полезность, имеющая вид , будет конечна (ряд сходится). Однако он не ставил перед собой задачи измерения полезности, и не пытался объяснить, почему его принцип ожидаемой полезности можно считать рациональным. Вместе с тем эту теорию впоследствии неизменно отвергали как правильное объяснение, - обычно потому, что господствующее убеждение в убывающей предельной полезности заставляло считать, что существование азартных игр не может быть объяснено таким образом.

Теория Бернулли как таковая является главным образом описательной моделью, хотя для своего времени сам принцип ожидаемой полезности мог выглядеть вполне убедительно.

Формальное доказательство того, что принцип максимизации ожидаемой полезности является критерием рациональности принимаемых решений, т.е. может быть выведен из нескольких аксиом, было проведено лишь в 1947 году Джоном фон Нейманом и Оскаром Моргенштерном. В нем утверждается, что "в условиях, на которых базируется анализ кривой безразличия, легко определить численную полезность[6]", ожидаемое значение которой максимизируется в выборе среди альтернатив, предполагающих риск. И эта концепция применима к исходам любого рода, где денежные выигрыши являются лишь частным случаем (в отличие от модели Крамера и Бернулли). Именно эта общность теории, по мнению многих экономистов[7], и позволила ей стать основой анализа рисковых ситуаций.

Теория ожидаемой полезности Неймана и Моргенштерна строится на следующих аксиомах:

· Аксиомы полноты и транзитивности предпочтений. Если рисковая ситуация (далее РС) L₁ предпочтительней РС L₂, то это можно записать как L₁> L₂. Полнота означает, что индивид способен всегда оценить, какая РС для него предпочтительней, а какая нежелательней. Транзитивность заключается в то, что, если L₁> L₂, L₂> L₃, то L₁> L₃.

· Аксиома непрерывности. Если существуют такие исходы x₁,x₂,x₃ , что x₁>x₂>x₃, существует такая вероятность p для x₁, а для x₃ –вероятность (1-p), что РС (x₁, p; x₃, (1-p)) столь же привлекательно, как РС с гарантированным исходом x₂. То есть при определенной p индивиду будет всё равно, точно получить какой-то результат или иметь риск получить результат лучше или хуже.

· Аксиома независимости. Если существуют две РС – L₁(x₁, p; x₃, 1-p) и L₂(x₂,p; x₃, 1-p), где x₁, x₂ могут или связаны, или не связаны с риском – и x₁=x₂ (равнозначны), то и L₁=L₂ независимо от x₃.

· Если в РС L₁(x₁, p; x₂, 1-p) и L₂(x₁,q; x₂, 1-q) x₁>x₂, то L₁> L₂ тогда и только тогда, когда p>q.

· Принцип сведения составных РС. При принятии решения для человека не важен порядок, в котором представлены призы и вероятности в РС, а важно лишь конечное распределение призов в РС, сочетающееся с перемножением составных вероятностей.

Пяти вышеперечисленных аксиом, достаточно, чтобы гарантировать существование такого индекса полезности, при котором ранжирование РС по их ожидаемой полезности полностью соответствует действительным предпочтениям индивида, как считают  Д. Нейман и О. Моргенштерн.

Что касается самой функции полезности, то она является единственной с точностью до положительного линейного преобразования. Это означает, что если функция U(x) задает предпочтения индивида относительно исходов x, то функция U*(x) = aU(x)+ b, где a, b – числовые коэффициенты, a > 0, также задает предпочтения индивида относительно x. Оказывается, если подвергнуть функцию ожидаемой полезности положительному линейному преобразованию, то полученная в результате этого функция не только будет представлять те же самые предпочтения, но и по-прежнему будет обладать свойством ожидаемой полезности.

Это также означает, что для этой функции нет зависимости от начала координат и единицы измерения. Например, мы можем произвольно считать началом координат $10 (т.е. положить U(10) = 0, и принять U(10 000) равной, скажем, 100 единицам полезности (ютилям)). Используя эти две точки отсчета, индекс полезности можно легко получить с помощью простых вопросов типа "Какой достоверный доход столь же привлекателен, что и лотерея 50/50 с исходами $10 и $10000?" Если эта сумма равна $x*, то U(x*) полагается равным 0,5U(10) + 0,5U(10 000) = 50 ютилям. До тех пор, пока такая пробная лотерея содержит исходы, полезность которых известна, мы можем определять значения полезности в других точках.

Важную роль в теории ожидаемой полезности играет понятие неприятия риска (подробнее в §5). Выпуклая вверх функция полезности, принимающая вид экспоненциальной кривой, характеризует неприятие риска, а выпуклая вниз – стремление к риску.

С точки зрения измерения полезности теория Неймана и Моргенштерна является кардиналистской, поскольку ее шкала полезности является интервальной. Однако с точки зрения предпочтений, её можно трактовать как ординалистскую, поскольку она обеспечивает лишь порядковое ранжирование лотерей. Поэтому к кардиналистской составляющей теории следует относиться аккуратно. Хотя функции полезности представляют собой интервальные шкалы, т.е. отношения разностей между уровнями полезности независимы относительно линейных преобразований, – это не означает, например, что из x₁ > x₂ > x₃ > x₄ и U(x₁) – U(x₂) > U(x₃) – U(x₄) следует, что перемещение из x₁ в x₂ должно быть более предпочтительным, чем перемещение из x₃ в x₄. Поэтому полезность по Нейману и Моргенштерну нельзя интерпретировать как измерение силы предпочтения в условиях определенности, что качественно отличает ее от неоклассической кардинальной полезности. Это объясняется тем, что предпочтения определяются по крайней мере двумя различными факторами, а именно: 1) силой предпочтений достоверных исходов; и 2) отношением к риску. Функция полезности Неймана и Моргенштерна является составной комбинацией этих двух факторов, которая не требует ни прямого сопоставления интервалов, ни измерения силы предпочтений. Как теория предпочтений она является всецело ординалистской. Тем не менее, она неявно предполагает, что существует полезность неоклассического кардиналистского типа – иначе было бы психологически невозможно определить достоверный эквивалент рисковых ситуаций.

Существует, еще множество концепций ожидаемой полезности, имеющих различие в функциях полезности, но все так или иначе являются модификацией именно этой модели. Об остальных вскользь упоминается чуть ниже.

Другой аспект модели ожидаемой полезности, в котором наблюдаются различные точки зрения – это определение вероятностей. В аксиоматике теории Неймана и Моргенштерна вероятность рассматривается как элементарное понятие, численное значение которого определено объективно. Однако эмпирически понятие вероятности является куда более проблематичным как с философской, так и с практической точек зрения. Чтобы убедиться в этом, рассмотрим коротко четыре основные концепции вероятности и пределы возможностей каждой из них.

Первая – это классическая концепция Пьера Лапласа, который определил вероятность как число благоприятных элементарных исходов некоторого события, отнесенное к числу всех возможных элементарных исходов. К недостаткам этой теории можно отнести то, что это определение нелегко применить в случае бесконечного пространства исходов, и оно практически ограничивается только хорошо структурированными ситуациями. К положительным моментам, разумеется, относится формальная наглядность и относительная простота этой модели.

Якоб Бернулли, дядя Даниила Бернулли, еще раньше избежал этой тавтологии, отличив само понятие от его измерения. Он определил вероятность как "степень доверия", которая для каждого события может разниться у разных людей. Тем не менее он полагал, что искусство угадывания заключается в том, чтобы уточнять оценки неизвестных вероятностей, в частности, исследуя объективные частоты. Этот частотный подход позже был положен в основу аксиоматики Джона Венна, Ханса Рейхенбаха и Рихарда фон Мизеса которые определяли вероятность как предельное значение процента благоприятных исходов в бесконечной последовательности независимых испытаний. Такой подход является ограниченным по крайней мере с двух точек зрения. Во-первых, вероятность никогда не бывает точно измеримой численно – в лучшем случае ее можно оценить на очень большой выборке. Во-вторых, часто бывает непонятно, что следует считать пространством возможных исходов – так, если оценивается объективная вероятность попасть в авиакатастрофу, то следует ли брать все предыдущие полеты, или же только на этом маршруте, на этом типе самолета, в это время года и т.д.

Третью попытку определить вероятность объективно предприняла так называемая логическая школа Джона Мейнарда Кейнса и Гарольда Джеффриса. Эти авторы утверждали, что каждое множество эмпирических данных находится в логическом, объективном отношении к истинности некоторой гипотезы (например, о виновности кого-либо), даже если эти данные сами по себе не позволяют прийти к определенным выводам. Вероятность измеряет силу этой связи с точки зрения рационального индивида. Поскольку все три вышеописанных подхода привлекательны с определенных точек зрения, было предпринято немало попыток соотнести их друг с другом. Рудольф Карнап разработал формальную теорию согласованной системы приобретения нового знания, основанную на байесовском подходе, в которой совмещаются объективный и субъективный подходы. Гленн Шэфер подошел к объединению этих подходов с другой стороны – посредством формального различения разных типов вероятностей, делая упор на принципиальное отличие вероятности случайных событий от степени убежденности в наступлении тех или иных событий. Эта последняя концепция  является основополагающей для субъективизма, четвертой традиции, о которой следует упомянуть.

Субъективная, или персоналистская доктрина вероятности изначально разрабатывалась Фрэнком Рамсэем, Бруно де Финетти, Леонардом Сэвиджем и Праттом, Райффой и Шлайфером. С их точки зрения вероятности – это степени убежденности в том, что наступят те или иные события – как повторяющиеся, так и уникальные (например, третья мировая война). Данному множеству гипотез в принципе можно приписать любые субъективные вероятности при соблюдении некоторых условий рациональности. В отличие от других доктрин, эти условия рассматриваются здесь как достаточные и необходимые одновременно, без каких-либо дополнительных ограничений, накладываемых по логическим или эмпирическим соображениям. Основная аксиома совместимости, принятая в теории субъективной вероятности, – это согласованность предпочтений. Эта аксиома означает, что вероятности элементарных событий дают в сумме единицу, и что взаимодополняющие и взаимоисключающие события следуют с вероятностью, равной соответственно произведению и сумме элементарных вероятностей. В этом свете субъективные вероятности с математической точки зрения ничем не отличаются от других типов вероятности. Субъективная школа выработала процедуру одновременного измерения полезности и вероятности, основанную на выявленных предпочтениях.

Как видим, вероятность – не такое уж простое понятие. Ее измерение, очевидно, – нелегкое дело даже в некоторых вероятностных играх, не говоря уже о реальном мире. Чтобы отличать субъективную вероятность от объективной, первую из них мы будем обозначать f(p). Преобразование f() показывает, что вероятности, используемые в модели ожидаемой полезности, могут отличаться от установленных или тех, которые исследователь полагает объективными. Однако не все такие преобразования f(p_i), обладающие свойствами вероятностей (таким, как Σf(p_i) = 1), должны рассматриваться как степени убежденности в том, что события наступят. В литературе преобразования f(p_i) обычно используются в качестве показателей отношения к риску; для исследования симметричности компонент вероятности и ожидаемого исхода в моделях ожидаемой полезности; чтобы отразить предпочтения в отношении вероятностей и/или дисперсий, наконец, просто чтобы эмпирические данные можно было согласовать с предпосылкой нелинейности предпочтений по вероятности. Хотя эти разнообразные модели, как правило, относят к теории субъективной ожидаемой полезности, преобразование f(p_i) не обязательно должно являться мерой степени убежденности. Помимо преобразований, которые сохраняют математические свойства вероятности, существует много теорий, в которых это требование ослаблено. В Приложении Д эти преобразования вероятностей обозначены w(p_i), – мы будем называть их весами решений. Причем веса решений – это не вероятности: по словам Дэниэля Канемана и Амоса Тверски, они не подчиняются аксиомам вероятностей, и не должны интерпретироваться как меры убежденности. В их теории перспектив веса решений вводятся для того, чтобы отразить влияние событий на общую привлекательность игр – поэтому они монотонны по вероятности, но не обязательно линейны.

Подводя итоги, можно отметить, что полезность и вероятность по-разному трактуются в моделях ожидаемой полезности. Теоретическая концепция этой своеобразной психологии риска прошла последовательно четыре этапа:

а) На первом этапе считалось, что значение неопределенной перспективы равно придаваемому ей математическому ожиданию денежных значений выигрышей: 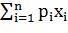   т.е. их средней, взвешенной по объективными вероятностям.

б) На втором этапе стали учитывать психологические значения выигрышей, которые заменили денежные значения в предыдущей формуле. Тем самым было предложено выражение где p i – объективные вероятности, а 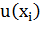 психологические значения в зависимости от исхода (выигрыша). Основными идеологами этой модели являются Бернулли, Нейман и Моргенштерн (разницей лишь в видах функции ).

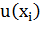в) На третьем этапе была высказана идея, что индивид оперирует не объективными вероятностями, а психологическими представлениями о них, т.е. субъективными вероятностями. Так возникла формула  –, где 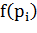 - субъективные вероятности. Эта формула остается еще вида формулы Бернулли, но объективные вероятности уже заменены субъективными.

г) На четвертом этапе, наконец, пришли к тому, что следует учитывать не только средневзвешенные по вероятностям психологические значения 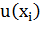 , но также и функцию распределения вероятностей, откуда следует формула
.

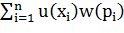В Приложении Д показаны основные модели ожидаемой полезности, существующие на данный момент. Основными различиями в моделях, как говорилось в начале параграфа, являются разновидности функций полезности и вероятности. Существуют и другие различия: например, в теории перспектив исходы x_i определяются как изменение финансового положения, а не итоговой величины богатства индивида. Кроме того, в описательных моделях пространство исходов может включать такие измерения, как сожаление, обоснованность выбора и т.д. Большинство из перечисленных моделей возникли как описательные, за исключением разве что моделей Неймана-Моргенштерна и Сэвиджа. Наверное, благодаря именно этому практическое использование закрепилось в основном за этими двумя моделями.

Как описательная модель, ориентированная на постижение процесса принятия решения, теория ожидаемой полезности несостоятельна по крайней мере с двух точек зрения.

 Во-первых, люди не рассматривают все проблемы как единое целое, как это полагает теория ожидаемой полезности. При выборе в условиях неопределенности индивид физически не способен принимать в расчет все возможные исходы, потому что попросту не имеет информации о них.

Во-вторых, они не обрабатывают информацию, особенно вероятности, в соответствии с принципами ожидаемой полезности (существуют масса исключений в поведении людей, которые невозможно описать с помощью данных функций полезности или вероятности).

Помимо этого сложность вызывает построение функции полезности Неймана-Моргенштерна. Использование в качестве стандарта лотерей с вероятностью 50/50 зачастую приводит к иным функциям полезности, чем, например, при использовании лотерей с вероятностями 30/70. Установлено, что весьма незначительные изменения в контексте или общих условиях формулировки проблемы могут привести к совершенно иным предпочтениям. Таким образом, встает вопрос еще и о том, в каком из контекстов следует измерять "истинное" отношение к риску; или, в более фундаментальной постановке, существуют ли в действительности неизменные вкусы и предпочтения, которые были бы совместимы с аксиомами ожидаемой полезности.

Однако нет правил без исключений. Для хорошо структурированных повторяющихся ситуаций со значительными ставками, в которых решения принимают хорошо подготовленные специалисты, максимизация ожидаемой полезности может хорошо описывать действительный процесс принятия решения, – например, если речь идет о бурении нефтяных скважин. Действительно, в крупных организациях, где используются компьютеры и работают высококвалифицированные менеджеры, модель ожидаемой полезности может использоваться в явном виде. Однако даже в таких благоприятных условиях постановки проблем и их решения могут быть искажены, если учесть невозвратные издержки, эффекты изоляции, асимметричность оценок альтернативных и непосредственных издержек и прочие косвенные факторы.

И всё же если бы не было самой теории ожидаемой, большая часть вышеупомянутых исследований не имела бы место. Модель как таковая породила более глубокие идеи и поставила более тонкие вопросы как описательного, так и нормативного характера относительно принятия решений в условиях риска. Она выявила тот факт, что люди воспринимают и решают проблемы иначе, и предложила схему и язык, в рамках которых обсуждаются эти расхождения. Впрочем это не меняет того факта, что нынешний статус общепринятой концепции в некоторых областях применения может быть поставлен под вопрос. Тем не менее, пока не созданы более удачные модели рациональности, максимизация ожидаемой полезности, несомненно, может оставаться ценным ориентиром, с которым можно сравнивать и по которому можно корректировать реальное поведение. Вместе с тем, возможно, что нынешние парадоксы и устойчивые нарушения ожидаемой полезности содержат в себе семена будущих нормативных и описательных теорий выбора. В конце концов, ведь именно парадокс Бернулли породил нынешнюю модель ожидаемой полезности.

Отношение к риску.

В предыдущем параграфе были рассмотрены основные модели общей полезности. Отличия в них по сути заключались в различных функциях психологических преобразований объективных переменных: вероятности и исхода рисковой ситуации. То есть многие экономисты пытались максимально отождествить формальную математическую функцию и поведение [рационального] человека.

Говоря о психологическом восприятии индивидуумом действительности (в нашем случае рисковой ситуации) принято рассматривать две отклоняющиеся от нормальной ситуации типологии поведения.

О первой, неприятии риска, было упомянуто еще в модели ожидаемой полезности Неймана-Моргенштерна. Именно в этой модели впервые принимается во внимание психологический эффект, производящий влияние на функцию полезности. Противником риска считается человек, который предпочитает рисковой ситуации результат, равный ожидаемому значению исходов. Это означает, что для этого человека полезность ожидаемого дохода больше ожидаемой полезности рисковой ситуации. Иначе говоря, если такому человеку предложить одно из двух: либо 10 рублей, либо 5 рублей с вероятностью 50% и 15 рублей с вероятностью 50%, - то он выберет 10 рублей и избежит рисковой ситуации. То есть 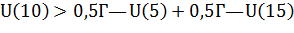. Графически эта ситуация изображена в Приложении Е. Выпуклая вверх функция – кривая полезности для индивида, который не является сторонником риска. Причем существует прямо пропорциональная зависимость между степенью неприятия и выпуклостью функции. Для такого вида функции производная первого порядка  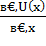будет убывающей величиной. Каждое равное увеличение дохода будет порождать всё меньшие увеличения полезности (это видно на графике).

Стоит отметить, что для определения степени неприятия риска (степени выпуклости вверх функции U(x)) был введен коэффициент Эрроу-Пратта (независимо друг от друга Arrow, 1971 и Pratt, 1964). Он представлен в Приложении З. Являясь константой для линейных и экспоненциальных функций, этот коэффициент отражает важный момент – психологическое восприятие рисковой ситуации (неприятие, предпочтение) не зависят от исходов (результатов).

Что же касается уже упомянутой ситуации предпочтения риска, то она обратна вышеописанному случаю. То есть психологическое восприятие рисковой ситуации таково, что функция полезности такового индивида принимает вид выпуклой вниз экспоненциальной функции. В той же рисковой ситуации (Приложение Ж) полезность ожидаемого дохода U(10) будет ниже ожидаемой полезности этой рисковой ситуации 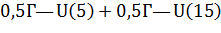, что будет толкать индивида идти на риск. Для этого вида функции U(x) производная первого порядка 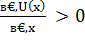. Это означает, что с каждым одинаковым увеличением дохода полезность будет увеличиваться всё больше и больше. Теоретически коэффициент Эрроу-Пратта можно использовать и для ситуации предпочтения риска.

На практике восприятия или отношение к риску можно увидеть воочию. Например, в ситуации выбора способа заработка. Бόльшая часть населения стран с рыночной экономикой пытаются найти такие положения, при которых в наименьшей степени возможно снижение уже имеющегося благосостояния. Поэтому эта же бόльшая часть населения предпочитает относительно стабильный заработок наемного работника ненадежному предпринимательскому доходу.

Основная причина этого состоит в том, что высокие прибыли, которые сулит частное предпринимательство, никто не гарантирует. И, отдавая свои предпочтения стабильным заработным платам, более низким, чем возможные прибыли предпринимательской деятельности, индивидуумы имеют возросшие альтернативные издержки. Можно сказать, что такие издержки идут на уменьшение риска.

Конечно, нельзя назвать такое поведение нерациональным. В условиях постоянных расходов для многих стабильность доходов является высшим приоритетом, которым нельзя пожертвовать ради увеличения богатства в будущем. В России эта ситуация подкрепляется еще и не самыми благоприятными условиями для предпринимательства, по разным оценкам, заключающимися в высокой степени нестабильности.