Лемма 3.3 Предположим, что ненулевое комплексное число 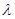 принадлежит спектру оператора Т. Тогда
принадлежит спектру оператора Т. Тогда  является собственным значением оператора Т*.
является собственным значением оператора Т*.
Доказательство. Применяя предыдущую лемму, получим, что множество значений оператора (  I–Т) не совпадает со всем пространством. Так как множество значений оператора (
I–Т) не совпадает со всем пространством. Так как множество значений оператора (  I –Т) замкнуто, то существует ненулевой элемент у такой, что для любого x
I –Т) замкнуто, то существует ненулевой элемент у такой, что для любого x  H справедливо равенство [
H справедливо равенство [  х–Тх, у] = 0, или [х,
х–Тх, у] = 0, или [х, 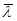 у–Т*у] = 0. Таким образом,
у–Т*у] = 0. Таким образом,  является собственным значением оператора Т. Из вышеприведенных лемм следует следующая теорема
является собственным значением оператора Т. Из вышеприведенных лемм следует следующая теорема
Теорема 3.1 Пусть  – ненулевое комплексное число. Тогда либо
– ненулевое комплексное число. Тогда либо 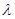 является собственным значением оператора Т, либо оно принадлежит его резольвентному множеству. (Это утверждение называется альтернативой Фредгольма.)
является собственным значением оператора Т, либо оно принадлежит его резольвентному множеству. (Это утверждение называется альтернативой Фредгольма.)
Доказательство. Достаточно показать, что если число 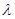 принадлежит спектру оператора Т, то оно является собственным значением. Если
принадлежит спектру оператора Т, то оно является собственным значением. Если 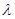 не принадлежит спектру T и не является собственным значением, то множество значений оператора (
не принадлежит спектру T и не является собственным значением, то множество значений оператора (  I–Т) не совпадает со всем пространством. Согласно предыдущей лемме отсюда следует, что
I–Т) не совпадает со всем пространством. Согласно предыдущей лемме отсюда следует, что  является собственным значением сопряженного оператора T٭. Применяя лемму 2.3 еще раз, получим, что
является собственным значением сопряженного оператора T٭. Применяя лемму 2.3 еще раз, получим, что 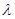 является собственным значением оператора T ** = T . Теорема доказана.
является собственным значением оператора T ** = T . Теорема доказана.
Лемма 3.4 Пространство собственных функций, отвечающих ненулевому собственному значению, конечномерно.
Доказательство. Пусть  – ненулевое собственное значение. Предположим, что соответствующее пространство собственных функций бесконечномерно. Пусть {ек}— ортонормальный базис этого подпространства. Тогда Tek =
– ненулевое собственное значение. Предположим, что соответствующее пространство собственных функций бесконечномерно. Пусть {ек}— ортонормальный базис этого подпространства. Тогда Tek =  ek , и потому [ Tek , ek ] =
ek , и потому [ Tek , ek ] =  . Но последовательность { Tek } должна сильно сходиться к нулю, что невозможно.
. Но последовательность { Tek } должна сильно сходиться к нулю, что невозможно.
Лемма 3.5 Последовательность {Хп} ненулевых и попарно различных собственных значений оператора Т может иметь предельной точкой лишь нуль.
Точно так же, как и в конечномерном случае, собственные векторы, соответствующие различным собственным значениям, линейно независимы. Действительно, пусть Тх =  х, Тх2 =
х, Тх2 =  х2, Txm =
х2, Txm = 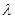 xm . Пусть, далее, m является наименьшим целым числом таким, что элемент хт принадлежит подпространству, порожденному элементами {х, .., Хт-1). Тогда
xm . Пусть, далее, m является наименьшим целым числом таким, что элемент хт принадлежит подпространству, порожденному элементами {х, .., Хт-1). Тогда
xm 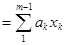 (3.9)
(3.9)
Следовательно,
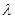 xm =
xm = 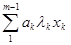 (3.10),
(3.10),
и потому
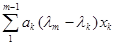 =0 (3.11)
=0 (3.11)
Отсюда следует, что т может быть уменьшено на единицу, что противоречит определению целого m. Обозначим через Рт оператор проектирования на подпространство Ет, порожденное элементами {х, ..., хт}. Оператор Т отображает подпространство Е m в себя. Положим zm = xm — Pm -1 xm . Тогда zm 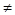 0 и [ Tzm ; zm ] = [
0 и [ Tzm ; zm ] = [ 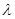 zm ; zm ]. Пусть em = zm /|| zm ||. Последовательность { em }, очевидно, ортонормальна и [ Tem , em ]= λm . Следовательно, λm→0. Таким образом, ненулевые собственные числа образуют изолированное подмножество спектра. Для произвольных двух заданных чисел 0<r 2 < r 2 множество { z: z <| z |< r 2 } может содержать лишь конечное число собственных чисел оператора Т. Таким образом, справедлива следующая теорема.
zm ; zm ]. Пусть em = zm /|| zm ||. Последовательность { em }, очевидно, ортонормальна и [ Tem , em ]= λm . Следовательно, λm→0. Таким образом, ненулевые собственные числа образуют изолированное подмножество спектра. Для произвольных двух заданных чисел 0<r 2 < r 2 множество { z: z <| z |< r 2 } может содержать лишь конечное число собственных чисел оператора Т. Таким образом, справедлива следующая теорема.
Теорема 3.2 Спектр компактного оператора содержит не более счетного числа точек и его предельной точкой может быть лишь нуль. Каждая ненулевая точка спектра является собственным значением.
Компактный оператор может вообще не иметь собственных значений. Однако для самосопряженных компактных операторов это уже не так.
Теорема 3.3 Самосопряженный компактный оператор, отображающий пространство Н в себя, имеет по крайней мере одно собственное значение.
Доказательство. Прежде всего докажем, что если оператор самосопряжен, то
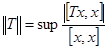 (3.12)
(3.12)
Обозначим правую часть этого равенства через с. Ясно, что с  . Далее, имеем
. Далее, имеем
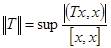 , х, у
, х, у 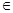 Н.
Н.
По
[Тх, у] + [Ту, х] = 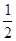 {[Т(х + у), х+у]–[Т(х-у), х–у]}.
{[Т(х + у), х+у]–[Т(х-у), х–у]}.
Следовательно,
|[Тх, у] + [Ту,х]|≤1/2{|[Т(х + у), х+у] + [Т(х-у),х-у]|}≤
≤ 1/2 c {|| x + y ||2+|| x – y ||2}= c (|| x ||2+|| y ||2) (3.13)
Tак как оператор Т самосопряжен, поэтому в случае вещественного гильбертова пространства
|[Тх, у]|≤ c 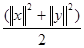 ,
,
или |[Тх, у]|≤с для всех || х || = || у || – 1. Следовательно, или |[Тх, у]|≤с|| х || *|| у ||, или || T || < с. Если исходное пространство рассматривается над полем комплексных чисел, то положим [ Tx , у] = | [Тх, у] | ei  . Пусть х1 = x
. Пусть х1 = x  . Тогда в силу самосопряженности оператора T имеем
. Тогда в силу самосопряженности оператора T имеем
[Т x 1 , y 1 ] + [Ту, х1] = с(  ) (3.14)
) (3.14)
Полагая || х || = || у || = 1, получим [ Tx , у] 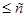 , отсюда следует, что | [Тх, у] | < с|| х || || у || . Таким образом существует последовательность {хп} такая, что
, отсюда следует, что | [Тх, у] | < с|| х || || у || . Таким образом существует последовательность {хп} такая, что
|| х n ||= 1, lim |[ Txn , xn ]| = || T ||>0
Tак как последовательность {[Тхт, хт]} состоит из вещественных чисел, то, переходя к подпоследовательности, можно считать, что она сходится либо к +||T||, либо к –||Т||. Обозначим этот предел через  . Еще раз переходя к подпоследовательности можно считать, что х0 слабо сходится к х0; в силу компактности оператора Т последовательность {Тхп} будет сильно сходиться к у0 =Тх0. Следовательно,
. Еще раз переходя к подпоследовательности можно считать, что х0 слабо сходится к х0; в силу компактности оператора Т последовательность {Тхп} будет сильно сходиться к у0 =Тх0. Следовательно,
lim [ Txm , xm ] = [Тхо, хо] = [у0, х0] (3.15)
Кроме того,
0< lim || Txm –  xm ||2 = || y 0 ||2 - 2
xm ||2 = || y 0 ||2 - 2  2 +
2 +  2 = || у0 || 2 –
2 = || у0 || 2 – 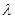 2.
2.
Но || у0 || 2 = lim || Txm ||2 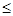 || T ||2 =
|| T ||2 = 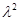 , поэтому || у0 || 2 =
, поэтому || у0 || 2 =  и
и
lim || Txm – 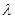 xm ||2 = 0 (3.16).
xm ||2 = 0 (3.16).
В силу сильной сходимости { Txm } последовательность {хт} сильно сходящаяся. Следовательно, Тх0 =  хо, причем ||х0||=1 и
хо, причем ||х0||=1 и 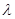 = ±|| T ||. Теорема доказана.
= ±|| T ||. Теорема доказана.
Точно так же, как и в конечномерном случае, собственные векторы самосопряженного оператора, соответствующие различным собственным значениям, ортогональны. Пусть теперь Т — компактный самосопряженный оператор. Тогда, как мы знаем, его спектр состоит из дискретного множества вещественных собственных значений { 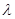 i } и предельной точкой {
i } и предельной точкой {  i } может быть лишь нуль. Обозначим через Mi подпространство собственных векторов, соответствующих ненулевому собственному значению
i } может быть лишь нуль. Обозначим через Mi подпространство собственных векторов, соответствующих ненулевому собственному значению  i .
i .
М i = {х : Тх = 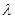 х}.
х}.
Пусть M 0 = {х: Тх = 0}. Для любого х из Н положим xi = Р i х, где Pi — оператор проектирования на подпространство Mi .
Тогда 0 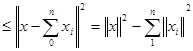 , потому ряд
, потому ряд 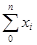 сильно сходится. Рассмотрим подпространство H0, ортогональное всем Mi , i= 0, 1, ... Тогда Н0 — замкнутое подпространство и оператор T, будучи самосопряженным, отображает Н0 в себя. Так как оператор Т является самосопряженным и компактным, то существует собственное значение
сильно сходится. Рассмотрим подпространство H0, ортогональное всем Mi , i= 0, 1, ... Тогда Н0 — замкнутое подпространство и оператор T, будучи самосопряженным, отображает Н0 в себя. Так как оператор Т является самосопряженным и компактным, то существует собственное значение 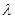 такое, что Тх =
такое, что Тх =  х, x
х, x 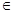 H. Однако это возможно лишь в том случае, если H 0 ={0}, т. е. нуль является единственным элементом H 0. Следовательно, для любого х из H справедливо разложение
H. Однако это возможно лишь в том случае, если H 0 ={0}, т. е. нуль является единственным элементом H 0. Следовательно, для любого х из H справедливо разложение
x = 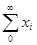 (3.17).
(3.17).
Следовательно, Tx =  . Заметим, что для каждого элемента
. Заметим, что для каждого элемента 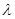 i справедливо разложение
i справедливо разложение
xi =  , Te
, Te  =
=  (3.18),
(3.18),
где е ij, j = 1, …, mi, –базис подпространства М i , которое, как было показано выше, конечномерно.
Замечание. Равенство Тх = 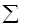
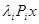 можно переписать в виде
можно переписать в виде
Т =  ,
, 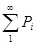 =I , [ Pix , Pjx ] = 0,
=I , [ Pix , Pjx ] = 0,
где I — тождественный оператор. Из этих равенств следует
T = 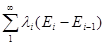 , Ei =
, Ei =  (3.19)
(3.19)
причем последовательность операторов проектирования { Ei } не убывает. Такого рода представление можно получить и для произвольного ограниченного оператора.
Пример 3.1 Задача определения собственных значений и собственных функций компактного самосопряженного оператора в общем случае довольно сложна и, за исключением отдельных случаев, может быть решена лишь численно. Здесь мы рассмотрим лишь простейшую итерационную процедуру, позволяющую решить эту задачу приближенно. Пусть Т—компактный самосопряженный оператор и х произвольный ненулевой элемент пространства Н. Предполагая Тх 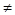 0, положим хп = Тпх/
0, положим хп = Тпх/ 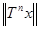 . Если Ттх = 0 для некоторого m, то элемент х должен принадлежать ядру оператора T, и потому он является собственным вектором. Таким образом, если элемент х не является собственным вектором, отвечающим нулевому собственному значению, то Тпх
. Если Ттх = 0 для некоторого m, то элемент х должен принадлежать ядру оператора T, и потому он является собственным вектором. Таким образом, если элемент х не является собственным вектором, отвечающим нулевому собственному значению, то Тпх  0 для любого п. Предположим, что это условие выполнено. Рассмотрим спектральное представление Tx =
0 для любого п. Предположим, что это условие выполнено. Рассмотрим спектральное представление Tx = 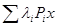 , где
, где 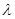 I –ненулевые собственные значения, а Pi —операторы проектирования на соответствующие подпространства собственных векторов. Предположим, что модули собственных значений образуют невозрастающую последовательность, т.е.
I –ненулевые собственные значения, а Pi —операторы проектирования на соответствующие подпространства собственных векторов. Предположим, что модули собственных значений образуют невозрастающую последовательность, т.е. 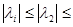 ... Определим оператор P
... Определим оператор P 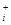 следующим образом. Если +|
следующим образом. Если +| 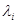 | является собственным значением, то Р
| является собственным значением, то Р 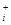 — оператор проектирования на соответствующее подпространство собственных векторов, в противном случае P
— оператор проектирования на соответствующее подпространство собственных векторов, в противном случае P  — нулевой оператор. Аналогично, если —|
— нулевой оператор. Аналогично, если —| 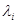 | — собственное значение, то Р
| — собственное значение, то Р 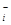 — проектор на соответствующее подпространство собственных векторов, иначе Р
— проектор на соответствующее подпространство собственных векторов, иначе Р 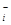 — нулевой оператор. Итак, пусть последовательность собственных значений упорядочена по возрастанию их модулей:
— нулевой оператор. Итак, пусть последовательность собственных значений упорядочена по возрастанию их модулей: 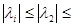 … Тогда ясно, что последовательность
… Тогда ясно, что последовательность
[Тхп, хп] = 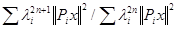
сходится к
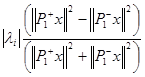 .
.
если только || P  x ||2 +
x ||2 +  0.
0.
Последовательность { x 2 n } сильно сходится к
( P 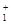 x + P
x + P 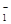 x )/|| ( P
x )/|| ( P 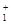 x – P
x – P 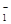 x )||
x )||
а последовательность х2n+1 сходится к
( P 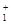 x + P
x + P 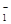 x )/|| ( P
x )/|| ( P 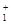 x – P
x – P 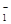 x )|| .
x )|| .
В более общем случае следует положить
k = inf { j : || P 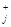 x + P
x + P 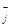 x ||
x ||  0}
0}
и во всех последовательностях, рассмотренных выше, вместо индекса 1 подставить k . С целью ускорения сходимости процесса можно исходить из оператора Т – 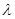 I вместо Т. Это и есть обобщение энергетического метода на бесконечномерный случай.
I вместо Т. Это и есть обобщение энергетического метода на бесконечномерный случай.
Заключение
Дата: 2019-12-10, просмотров: 400.