Определение 2.5 Ограниченный линейный оператор, отображающий пространство H 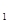 в H2, называется компактным (вполне непрерывным), если он переводит ограниченные множества из Н
в H2, называется компактным (вполне непрерывным), если он переводит ограниченные множества из Н 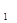 в компактные подмножества H 2 .
в компактные подмножества H 2 .
Важное характеристическое свойство компактных операторов определяется следующей теоремой [7].
Теорема 2.3 Пусть Т — компактный оператор, отображающий пространство H 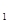 в H 2. Тогда для любой слабо сходящейся последовательности {хп} из Н
в H 2. Тогда для любой слабо сходящейся последовательности {хп} из Н 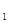 последовательность {Тхп} сильно сходится в H 2. Обратно, любой ограниченный линейный оператор, обладающий этим свойством, компактен [6].
последовательность {Тхп} сильно сходится в H 2. Обратно, любой ограниченный линейный оператор, обладающий этим свойством, компактен [6].
Доказательство. Пусть оператор Т компактен, а {хп} — слабо сходящаяся, скажем к х0, последовательность из Н 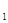 . Тогда, согласно принципу равномерной ограниченности имеем оценку
. Тогда, согласно принципу равномерной ограниченности имеем оценку
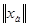 <М
<М
для некоторого числа М, О < М < 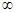 . Поэтому последовательность {Тхп} принадлежит некоторому компактному подмножеству в H2 и, значит, из любой ее подпоследовательности можно извлечь еще более узкую сильно сходящуюся подпоследовательность. Обозначим такую сильно сходящуюся подпоследовательность через { Txnk }, а ее предел через у. Тогда для любого h
. Поэтому последовательность {Тхп} принадлежит некоторому компактному подмножеству в H2 и, значит, из любой ее подпоследовательности можно извлечь еще более узкую сильно сходящуюся подпоследовательность. Обозначим такую сильно сходящуюся подпоследовательность через { Txnk }, а ее предел через у. Тогда для любого h 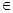 H 2 имеем цепочку равенств
H 2 имеем цепочку равенств
[ y , h ] = lim [ Txnk , h ] = lim [ xnk , T * h ] =[х0, T * h ] = [Тх0, h ],
откуда у=Тх0, так что у не зависит от выбора конкретной подпоследовательности, а значит,
limTxn = у.
Обратно, пусть Т — ограниченный линейный оператор, переводящий любую слабо сходящуюся последовательность в сильно сходящуюся. Пусть В— ограниченное множество в Н 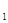 . Покажем, что замыкание множества ТВ компактно. Действительно, пусть {хп} — произвольная последовательность элементов из В. В силу свойства слабой компактности ограниченных множеств в гильбертовом пространстве найдется подпоследовательность { xnk }, слабо сходящаяся к некоторому пределу, скажем к x
. Покажем, что замыкание множества ТВ компактно. Действительно, пусть {хп} — произвольная последовательность элементов из В. В силу свойства слабой компактности ограниченных множеств в гильбертовом пространстве найдется подпоследовательность { xnk }, слабо сходящаяся к некоторому пределу, скажем к x 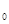 . Тогда подпоследовательность { Txnk } сходится сильно и, как мы видели, ее пределом должна быть точка Тх0. Очевидно, что T х0 — предельная точка множества ТВ, а это и значит, что оператор компактен.
. Тогда подпоследовательность { Txnk } сходится сильно и, как мы видели, ее пределом должна быть точка Тх0. Очевидно, что T х0 — предельная точка множества ТВ, а это и значит, что оператор компактен.
Пример 2.4 Пусть ( 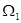 ,
,  ,
, 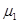 ), (
), ( 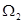 ,
, 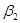 ,
, 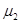 ) — пространства c
) — пространства c 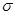 -конечными мерами
-конечными мерами 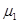 ,
, 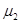 . Обозначим через R ( t , s )
. Обозначим через R ( t , s ) 
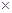
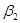 измеримую матричную функцию порядка (р, q), определенную на множестве
измеримую матричную функцию порядка (р, q), определенную на множестве 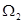
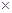
 . Положим
. Положим
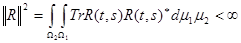 .
.
Тогда оператор L, определенный соотношениями
Lf=g, g(t)= 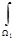 R(t, s) f (s)d
R(t, s) f (s)d 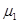 , t
, t 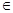 Q2,
Q2,
линейно и непрерывно отображает пространство Н1 = L 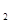 (
( 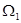 ,
, 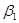 ,
, 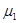 )p в H2= L2(
)p в H2= L2( 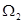 ,
, 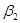 ,
, 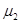 )p . Заметим, что пространство Н
)p . Заметим, что пространство Н 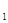 не обязательно сепарабельно. Докажем компактность оператора L. Пусть последовательность fn
не обязательно сепарабельно. Докажем компактность оператора L. Пусть последовательность fn 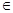 H 1 слабо сходится. Для всех t
H 1 слабо сходится. Для всех t 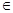
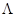 , где
, где 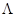 —множество полной меры имеем
—множество полной меры имеем
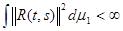 .
.
Пусть ei — единичный вектор евклидова пространства Rq. Тогда для любого t 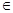
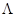 формула
формула
[  R ( t , s ) f ( s ) d
R ( t , s ) f ( s ) d 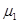 , е i ]
, е i ]
определяет линейный непрерывный функционал на пространстве H 1. Следовательно, для каждого t 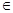
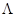 последовательность
последовательность
gn ( t )= 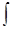 R ( t , s ) fn ( s ) d
R ( t , s ) fn ( s ) d 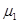
| сходится к |
|
|
g ( t ) = R ( t , s ) f ( s ) d 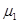 .
.
Можно применить теорему Лебега о почленном интегрировании последовательности. Следовательно,
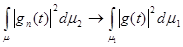
при n 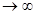 . Так как последовательность gn(∙) сходится к g(∙) слабо, то отсюда следует сильная сходимость gn к g.
. Так как последовательность gn(∙) сходится к g(∙) слабо, то отсюда следует сильная сходимость gn к g.
3 Спектральная теория компактных операторов
3.1 Множество значений компактного оператора
Спектральная теория характеризует спектры и резольвентные множества операторов. Исследование интегральных операндов по существу эквивалентно изучению интегральных уравнений.
По своим свойствам компактные операторы близки к конечномерным (матричным) операторам. Кроме того, последние играют большую роль в приложениях. Пусть Т— компактный оператор, отображающий пространство Н в себя. Тогда, если пространство бесконечномерно, то нуль должен принадлежать спектру, поскольку тождественный оператор Т-1Т не является компактным. Напомним, что в дальнейшем пространства рассматриваются над полем комплексных чисел.
Лемма 3.1 Для любого 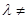 0 множество значений оперaтора
0 множество значений оперaтора 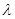 I – Т замкнуто [10].
I – Т замкнуто [10].
Доказательство. Пусть {уп} — сходящаяся последовательность из множества значений оператора ( 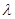 I— T), т. е. yn=
I— T), т. е. yn= 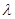 х n – Тхп. Положим
х n – Тхп. Положим
М = {х: 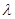 х=Тх}.
х=Тх}.
Тогда М – замкнутое подпространство Н. Обозначим через Р оператор проектирования на подпространство М и положим zn=хп –Рхп. Предположим, что ||zn|| 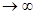 . Пусть
. Пусть
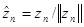 ,
,  (3.1).
(3.1).
В силу сходимости {уп} последовательность hn сходится к нулю. Так как || 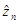 ||=1, то, переходя к подпоследовательности, можно считать, что {
||=1, то, переходя к подпоследовательности, можно считать, что { 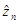 } слабо сходится к элементу
} слабо сходится к элементу 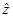 . Однако ввиду равенства ТР=
. Однако ввиду равенства ТР= 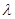 Р справедливо соотношение
Р справедливо соотношение
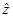 n = ( hn + T
n = ( hn + T 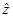 n )/
n )/ 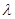 (3.2).
(3.2).
Отсюда, в силу сильной сходимости T 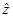 n к T
n к T 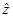 n следует, что последовательность {
n следует, что последовательность { 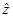 n } сильно сходится к
n } сильно сходится к 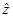 . Далее,
. Далее, 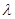
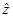 = T
= T 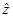 и ||
и || 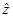 || = 1. Однако это невозможно, поскольку элементы
|| = 1. Однако это невозможно, поскольку элементы 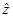 n принадлежат M
n принадлежат M 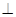 . Таким образом, последовательность {||zn||} ограничена. Поэтому, переходя к подпоследовательности, можно считать, что { zn } – слабо сходящаяся последовательность. Из равенства zn = ( yn + Tzn )/
. Таким образом, последовательность {||zn||} ограничена. Поэтому, переходя к подпоследовательности, можно считать, что { zn } – слабо сходящаяся последовательность. Из равенства zn = ( yn + Tzn )/ 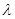 как и ранее, следует, что последовательность { zn } сходится сильно. Обозначая через z соответствующий предел, получим, что
как и ранее, следует, что последовательность { zn } сходится сильно. Обозначая через z соответствующий предел, получим, что 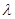 z = Tz + у, где у — предел последовательности {уп}. Лемма доказана.
z = Tz + у, где у — предел последовательности {уп}. Лемма доказана.
Лемма 3.2 Предположим, что 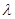
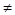 0 и множество значений оператора (
0 и множество значений оператора ( 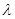 I –Т) совпадает со всем пространством Н. Тогда
I –Т) совпадает со всем пространством Н. Тогда 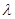 принадлежит резольвентному множеству оператора Т [10].
принадлежит резольвентному множеству оператора Т [10].
Доказательство. Достаточно показать, что 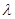 не является собственным значением оператора Т. Предположим противное; тогда найдется элемент х
не является собственным значением оператора Т. Предположим противное; тогда найдется элемент х 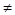 0 такой, что
0 такой, что 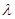 х=Тх. Так как множество значений оператора
х=Тх. Так как множество значений оператора 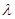 I–Т совпадает со всем пространством, то существует элемент f 1 из H такой, что
I–Т совпадает со всем пространством, то существует элемент f 1 из H такой, что 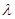 f 1–Tf 1 = x . Далее, по той же причине найдется элемент f2 такой, что
f 1–Tf 1 = x . Далее, по той же причине найдется элемент f2 такой, что 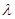 f 2–Tf 2 = f 1 . По индукции строится последовательность { fk } такая, что
f 2–Tf 2 = f 1 . По индукции строится последовательность { fk } такая, что
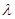 fk – Tfk = fk-1 (3.3)
fk – Tfk = fk-1 (3.3)
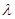 f1 – Tf1 =x=f0 (3.4)
f1 – Tf1 =x=f0 (3.4)
Обозначим через Ek подпространство, порожденное элементами { f 0,...,fk }. Докажем, что dim Ek > dim Ek для всех k 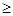 1. Для этого достаточно показать, что элемент fk не принадлежит пространству Ek -1 . Предположим противное. Тогда
1. Для этого достаточно показать, что элемент fk не принадлежит пространству Ek -1 . Предположим противное. Тогда
fk=  (3.5)
(3.5)
Следовательно,
Tfk =  aiTfi =
aiTfi = 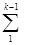 ai [
ai [ 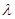 fi –fj-1] + a0
fi –fj-1] + a0 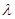 f0 (3.6).
f0 (3.6).
С другой стороны, Tfk = Xfk — Tfk -1 . Таким образом,
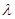 fk –fk -1 = –
fk –fk -1 = – 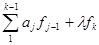 (3.7)
(3.7)
или
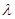 fk –fk -1 =
fk –fk -1 = 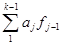 (3.8).
(3.8).
Следовательно, противоположное утверждение остается верным для ( k–1), и потому оно справедливо и для случая k = 1, что невозможно. Далее, если dimEk > dim Ek -1 , то существует ортонормированная последовательность векторов {е k } такая, что ek ортогонален подпространству Ek -1 . Но [ 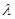 I – T ] Ek
I – T ] Ek 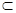 Ek -1 и потому [(
Ek -1 и потому [( 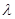 I — Т)ек, ek ] = 0, т. е.
I — Т)ек, ek ] = 0, т. е. 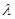 = [ Tek, ek ]. Но последовательность { ek } слабо сходится к нулю, поэтому последовательность { Tek } сходится к нулю сильно. Следовательно
= [ Tek, ek ]. Но последовательность { ek } слабо сходится к нулю, поэтому последовательность { Tek } сходится к нулю сильно. Следовательно 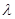 = 0, что невозможно.
= 0, что невозможно.
Дата: 2019-12-10, просмотров: 352.