Теорема 2.2 Пусть Т — ограниченный оператор, отображающий пространство Н в себя. Тогда 
 р(T) , если |
р(T) , если |  |>r, где r = lim
|>r, где r = lim 
 . Число г>0 называется спектральным радиусом оператора Т [5]
. Число г>0 называется спектральным радиусом оператора Т [5]
Доказательство. Основной шаг заключается в доказательстве сходимости ряда
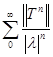 (2.2)
(2.2)
для всех |  |>г. Это непосредственно следует из того факта, что мажорирующий ряд
|>г. Это непосредственно следует из того факта, что мажорирующий ряд
 (2.3)
(2.3)
|
|
абсолютно сходится при |z|> lim  . Следовательно, ряд сходится по норме пространства L (H,H). Более того, имеем так что
. Следовательно, ряд сходится по норме пространства L (H,H). Более того, имеем так что
(  I – T)(
I – T)( 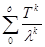 )=(
)=( 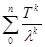 )(
)( 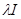 – T)=(
– T)=( 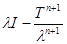 ) (2.4)
) (2.4)
Следствие 2.1 Спектр произвольного замкнутого оператора является замкнутым множеством. Спектр ограниченного оператора не пуст.
Доказательство. Сначала докажем, что резольвентное множество произвольного замкнутого оператора открыто. В случае, если резольвентное множество замкнутого оператора пусто, то доказывать нечего. Предположим, что резольвентное множество не пусто и содержит число  0. Покажем, что все
0. Покажем, что все 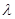 , удовлетворяющие условию |
, удовлетворяющие условию |  –
–  0|/||R(
0|/||R(  0; T )\\ < 1, принадлежат резольвентному множеству. Прежде всего, отметим, что для таких
0; T )\\ < 1, принадлежат резольвентному множеству. Прежде всего, отметим, что для таких  ряд
ряд 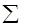 (
( 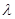 –
– 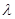 0)п R (
0)п R ( 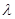 0; Т)п сходится и
0; Т)п сходится и
(I+ (  –
–  0) R (
0) R (  0; T))
0; T)) 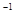 =
= 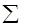 (
(  0–
0–  )
) 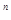 R(
R(  0; Т)п (2.5).
0; Т)п (2.5).
Докажем, что
 (2.6)
(2.6)
Пусть x  H. Имеем
H. Имеем
(  I – T ) (
I – T ) ( 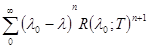 )x=x (2.7).
)x=x (2.7).
Если x  D(T), то
D(T), то
 (2.8).
(2.8).
Таким образом, оператор R ( λ ; T ) — резольвента. Следовательно, резольвентное множество открыто. Более того, имеем
R ( 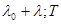 )=
)=  (2.9)
(2.9)
при ||λ R (λ0; T )||< 1.
Таким образом, если L(∙) — линейный непрерывный функционал на L ( H , H ), то функция L ( R ( K ; T )) оказывается аналитической на резольвентном множестве оператора Т. Рассмотрим теперь случай, когда оператор Т ограничен. Предположим, что его спектр — пустое множество. Тогда для любого линейного непрерывного функционала L (∙) аналитическая функция L ( R(λ;Т)) определена на всей комплексной плоскости и, кроме того, она ограничена в бесконечности, поскольку ||λR (λ; Т) ||≤(1–  /λ)-1 для всех |λ|>||Т||. Следовательно, в силу классической теоремы Лиувилля для любого функционала L (∙) и любого комплексного λ функция L ( R(λ;Т)) тождественно равна пулю. Но тогда L(I)=L(λR(λ;T)–TR(λ; I)) = L(TR(λ; T )). Поэтому в силу сходимости правой части последнего равенства к нулю при λ→ +
/λ)-1 для всех |λ|>||Т||. Следовательно, в силу классической теоремы Лиувилля для любого функционала L (∙) и любого комплексного λ функция L ( R(λ;Т)) тождественно равна пулю. Но тогда L(I)=L(λR(λ;T)–TR(λ; I)) = L(TR(λ; T )). Поэтому в силу сходимости правой части последнего равенства к нулю при λ→ + 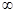 L ( I ) = 0 для любого линейного непрерывного функционала L (∙), что невозможно. Таким образом спектр ограниченного оператора не может быть пустым.
L ( I ) = 0 для любого линейного непрерывного функционала L (∙), что невозможно. Таким образом спектр ограниченного оператора не может быть пустым.
Определение 2.3 Ограниченный оператор называется квазинильпотентным, если его спектральный радиус равен нулю [6].
Спектр квазинильпотентного оператора содержит лишь нулевую точку.
Пример 2.2 Пусть H = L 2 (0, 1). Определим оператор Т соотношениями
Tf = g, g(t)= 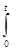 f(s)ds, 0
f(s)ds, 0 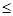 t
t 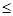 1 (2.10)
1 (2.10)
Тогда оператор Т линеен и ограничен. Используя неравенство Шиарца, найдем 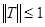 Что касается спектра оператора T, то заметим, что если
Что касается спектра оператора T, то заметим, что если
λf ( t )— 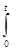 f ( s ) ds = 0 почти всюду на [0, 1],
f ( s ) ds = 0 почти всюду на [0, 1],
f — непрерывная функция. Далее, уравнение
λ f ( t )- 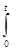 f ( s ) ds = g ( t )
f ( s ) ds = g ( t )
имеет единственное решение
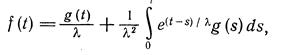 (2.11)
(2.11)
и потому спектр оператора Т может содержать лишь нулевую точку. Это можно доказать заметив, что оператор Т квазиниль-потентен:
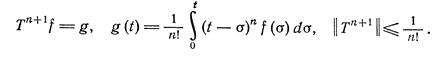 (2.12)
(2.12)
Как было доказано выше, спектр ограниченного оператора не может быть пустым. Следовательно, спектр оператора Т состоит из нулевой точки. С другой стороны, в рассматриваемом случае, нуль не является собственным значением, поскольку из условия Tf = 0 следует, что f = 0. Отсюда следует, что Т-1 — замкнутый линейный оператор, однако он неограничен. Это и следовало ожидать, поскольку T-1f = g означает, что g = f '.
Пример 2.3 В общем случае нельзя указать эффективной процедуры отыскания спектра и резольвентного множества заданного оператора. Однако, для интегральных операторов такой общий метод существует; он заключается в дифференцировании необходимое число раз равенства, определяющего точку спектра с целью получения определяющего дифференциального уравнения. Рассмотрим, например, оператор
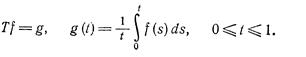 (2.13)
(2.13)
Рассмотрим сначала точечный спектр этого оператора. Если функция L(•) из H является собственным вектором, то
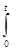 f ( s ) ds = λtf ( t ) почти всюду.
f ( s ) ds = λtf ( t ) почти всюду.
Дифференцируя обе части этого равенства, получим дифференциальное уравнение
f ( t ) = 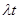
 +
+ 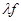 ( t ) ;
( t ) ;
его общее решение имеет вид f ( t )= k - ta , где k — произвольное постоянное число, а а = (1–λ)/λ. С другой стороны, из условия
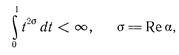
следует, что
l +2 Re ((1– λ)/ λ)=0 или Re (1/ λ)> 
Таким образом, всякое комплексное число λ, удовлетворяющее этому условию, принадлежит точечному спектру. Так как спектр — замкнутое множество, то {λ; -  + Re (1/ λ) ≥
+ Re (1/ λ) ≥  } принадлежит ему. Это множество представляет собой шар радиуса 1 с центром в точке
} принадлежит ему. Это множество представляет собой шар радиуса 1 с центром в точке  =1. Далее, рассмотрим уравнение
=1. Далее, рассмотрим уравнение 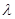 f — Tf = g , или
f — Tf = g , или
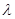 tf(t)-
tf(t)- 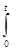 f(s)ds = tg (t),
f(s)ds = tg (t),
Предполагая дифференцируемость соответствующих функций,
получим
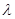 tf'(t) +
tf'(t) + 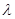 f (t)–f(t) = tg' (t) + g(t).
f (t)–f(t) = tg' (t) + g(t).
Отсюда следует, что
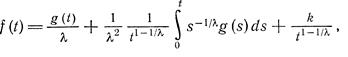 (2.14)
(2.14)
где k — константа. Если ограничиться рассмотрением тех 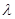 , для которых 1+2 Re (1-
, для которых 1+2 Re (1- 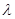 ) /
) / 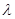 < 0, то, полагая k = 0, получим
< 0, то, полагая k = 0, получим
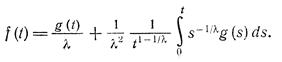 (2.15)
(2.15)
Условие 1 + 2 Re ( l — 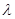 ) /
) / 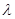 > 0 эквивалентно условиям Re ( l /
> 0 эквивалентно условиям Re ( l / 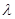 ) < C < 1/2, или
) < C < 1/2, или 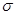 2 +
2 + 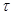 2 —2
2 —2  > 0, где
> 0, где 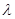 =
=  + i
+ i 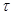 . Можно показать, что последняя формула определяет резольвенту. Заметим, что
. Можно показать, что последняя формула определяет резольвенту. Заметим, что  такое
такое 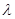 принадлежит спектру, но не является собственным значением. Безусловно, спектр целиком содержится в шаре |
принадлежит спектру, но не является собственным значением. Безусловно, спектр целиком содержится в шаре | 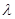 |
| 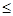 | T ||=2.
| T ||=2.
Определение 2.4 Ограниченный линейный оператор, отображающий пространство 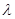 в себя, называется неотрицательно определенным, если он самосопряжен и квадратичная форма [Тх, х] неотрицательно определена.
в себя, называется неотрицательно определенным, если он самосопряжен и квадратичная форма [Тх, х] неотрицательно определена.
Для любого ограниченного линейного оператора операторы Т*Т и ТТ* неотрицательно определены [8].
Дата: 2019-12-10, просмотров: 348.