В математике функцией f с областью определения A и областью значений B называется множество упорядоченных пар (a,b)ÎA×B, таких, что если (a,b1)Îf и (a,b2)Îf, то b1 = b2. Множество упорядоченных пар может быть задано явно (перечислением) или неявно (например, свойствами пары или правилами вычисления).
Функцией в программировании называется конструкция, описывающая правила преобразования аргумента (входных параметров) в результат. Особенность, отличающая функцию состоит в том, что она возвращает значение, а её вызов может использоваться как операнд при вычислении выражения.
Побочным эффектом функции называется любое изменение функцией состояния программной среды, кроме возврата результата (изменение значений глобальных переменных, выделение и освобождение памяти, ввод-вывод и т. п.). Теоретически (с позиций функционального, а также структурного программирования) наиболее правильным является использование функций, не имеющих побочного эффекта (то есть таких, в результате вызова которых возвращается вычисленное значение, и только). На практике невозможно обойтись без функций с побочным эффектом, хотя бы для ввода-вывода.
В соответствии с парадигмой функционального программирования любая программа представляет собой набор вложенных вызовов функций, не вызывающих побочных эффектов.
Функции, выполняющие конкретные роли, могут быть достаточно общими, полезными при определении разных отображений, они могут получать имена для многократного использования в разных системах определений и могут быть разовыми, безымянными, применяемыми лишь один раз в конкретном месте.
3.2. Рекурсивные определения функции
В математической теории примитивно рекурсивных функций определяются базовые функции и два оператора (суперпозиции и примитивной рекурсии), позволяющие строить функции на основе уже имеющихся.
Оператор суперпозиции (иногда называется оператором подстановки). Пусть f — функция от m переменных, а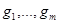 
— упорядоченный набор функций от n переменных каждая. Тогда результатом суперпозиции функций gk в функцию f называется функция h от n переменных, сопоставляющая любому упорядоченному набору 
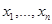значение
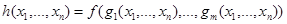
Оператор примитивной рекурсии. Пусть f— функция от n переменных, а g — функция от n + 2 переменных. Тогда результатом применения оператора примитивной рекурсии к паре функций f и g называется функция h от n + 1 переменной вида
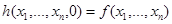
В данном определении переменную y можно понимать как счётчик итераций, f — как исходную функцию в начале итерационного процесса, выдающего некую последовательность функций n переменных, g — как оператор, принимающий на вход n переменных, номер шага итерации, функцию на данном шаге итерации, и возвращающий функцию на следующем шаге итерации.
Пример.Функция сложения двух натуральных чисел (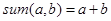 
) может быть рассмотрена в качестве примитивно рекурсивной функции двух переменных, получаемой в результате применения оператора примитивной рекурсии и подстановки
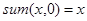
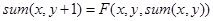
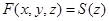
Функция следования S(x) – базовая функция одной переменной, сопоставляет любому натуральному числу x непосредственно следующее за ним натуральное число x + 1.
Умножение двух натуральных чисел (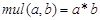 
) может быть рассмотрено в качестве примитивно рекурсивной функции двух переменных, получаемой в результате применения оператора примитивной рекурсии к функциям O и G. Нулевая функция O — без аргументов, всегда возвращает 0. G получается подстановкой в функцию сложения:
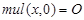
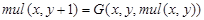
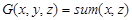
В программировании рекурсия это вызов функции или процедуры из неё же самой (обычно с другими значениями входных параметров), непосредственно или через другие функции (например, функция А вызывает функцию B, а функция B — функцию A). В ходе исполнения рекурсивной функции количество вложенных вызовов одной и той же функции или процедуры называется глубиной рекурсии. Глубина рекурсии – динамическая характеристика, меняющаяся в ходе вычисления и зависящая от входных аргументов.
Кроме глубины рекурсии рассматривается другая характеристика – порядок рекурсии. Функции, которые мы до сих пор определяли, будем называть функциями с рекурсией первого порядка. Далее, рекурсивно определим произвольный порядок рекурсии. Если в определении функции рекурсивный вызов k-го порядка является аргументом вызова этой же самой функции, то будем называть это рекурсией k+1-го порядка.
Пример.Гипероператор. Эта функция возникла в результате ответа на вопрос: «Что будет при продолжении стандартной последовательности математических действий?» сложение (+), умножение (×), возведение в степень (^). Сложение (+)является первым элементом последовательности (обозначим ее (1)), умножение (×) – вторым ((2)), соответственно, возведение в степень (^) – ((3)). Запишем функции для первых четырех элементов последовательности:
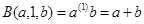
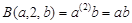
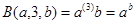
и рекурсивно определим общую операцию в инфиксной форме:
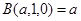
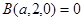
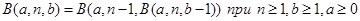
Данная функция, как видно из ее определения, является функцией с рекурсией второго порядка.
Пример.Функция Аккермана —вычислимая функция, которая не является примитивно рекурсивной. Она рекурсивно определяется с использованием рекурсии второго порядка следующим образом:
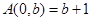
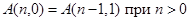
Данная функция связана с гипероператором следующим образом: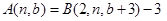 
.
При работе со списками используется специальный тип рекурсии, называемый «хвостовой рекурсией». В следующих примерах используем в качестве базовых, бинарную операцию «:», соединяющую голову и хвост списка, и функцию min, вычисляющую меньшее из значений двух заданных аргументов.
Пример.Функция конкатенации списков.
C((),y)=y
C(x:z,y)=F(x,y, C(z, y)),
где F(x, y, z)= x:z.
Здесь дано определение функции посредством математической формулы. Ранее данная функция уже описывалась на языке LISP (append) и будет далее описана на языке HASKELL.
Пример.Определение наименьшего элемента в списке методом попарных сравнений.
M((x))=x
M(x:y:())=min(x,y)
M(x:y:z)=M(min(x,y):M(z))
Данная функция использует хвостовую рекурсию второго порядка.
Дата: 2016-10-02, просмотров: 215.
