Определение функций и их вычисление в языке LISP основано на лямбда-выражениях, позаимствованных из лямбда-исчисления Черча, которое будет далее рассмотрено.
В лямбда-исчислении функция записывается в следующем виде:
λx1,x2,...,xN.fN .
В языке LISP лямбда-выражение (лямбда-форма) имеет вид:
(lambda (X1 X2 ... XN) FN)
Лямбда-форма предназначена для определения «безымянных» функций и называется вычисляемой функцией (Lambda - это не функция, лямбда-форма - это функция).
Первый аргумент лямбда-формы - (X1 X2 ... XN) является списком (возможно, пустым) формальных параметров.
Формальность параметров означает, что их можно переименовать и это не отразится на вычислениях, определяемых функцией.
Второй аргумент - FN называется телом. Оно представляет собой произвольное S-выражение, значение которого может вычислить интерпретатор языка LISP. Таким образом:
Для того, чтобы применить лямбда-функцию к аргументам, нужно в вызове функции поставить лямбда-выражение вместо имени функции:
((lambda (X1 X2 ... XN) FN) A1 A2 ... AN)
Здесь Ai (i=1,2,...,N) - выражения языка LISP, определяющие фактические параметры. Такую форму вызова функции называют лямбда-вызовом.
Функциональный язык программирования (каковым является LISP) предоставляет возможность реализации любого алгоритма записанного в виде определения функции. Например, функцию вычисления факториала можно определить с помощью лямбда-формы следующим образом:
(lambda (N) (if (= N 0) 1 (* N (fakt (- N 1)))))
Вычисление лямбда-вызова производится в два этапа. Вычисленные значения фактических параметров связываются с соответствующими формальными параметрами. Затем с учетом новых связей вычисляется тело лямбда-выражения, и полученное значение возвращается в качестве результата лямбда-вызова. Формальным параметрам после окончания вычисления возвращаются те связи, которые у них были перед вычислением лямбда-вызова.
Приведем несколько примеров лямбда- вызовов:
$ ((lambda (N) (+ N 1)) 45)
$ ((lambda (M N) (cond ((< M N) M) (T N))) 23 123)
$ (lambda nil (+ 3 5))
$ (lambda () (+ 3 5))
$ ((lambda (X) (eq X nil)) nil)
T
Лямбда-форма - это «безымянная» функция, которая пропадает тотчас же после лямбда-вызова. Ее нельзя использовать снова, так как нельзя вызвать по имени, хотя лямбда-вызов доступен как списочный объект.
«Безымянные» функции используются, например, при передаче функции в качестве аргумента другой функции или при формировании функции в результате вычислений.
2.7.2. Невычисляющие функции.
Один из самых эффективных путей реализации сложных программ в современных реализациях LISPа являются макросредства. С помощью макроопределений фактически задается закон предварительного построения тела функции непосредственно перед его исполнением.
Макросредства реализуются с помощью невычисляющих функций или nlambda-функций. nlambda -функция - специальный вид лямбда-выражения, обеспечивающий передачу параметров функции без их предварительного вычисления.
Интерпретация невычисляющих функций производится в два этапа.
На первом, который мы будем называть макрорасширением, происходит формирование лямбда-определения функции в зависимости от текущего контекста, на втором осуществляется интерпретация созданного лямбда-выражения.
nlambda -выражение имеет вид:
(nlambda (X1 X2 ... XN) FN)
Первый аргумент формы nlambda - (X1 X2 ... XN) является списком (возможно, пустым) формальных параметров.
Второй аргумент формы nlambda (FN) - это тело. Оно представляет собой произвольное S-выражение, значение которого может вычислить интерпретатор языка LISP. Таким образом:
Для того, чтобы применить nlambda – определение функции к аргументам, нужно в вызове функции поставить nlambda -выражение вместо имени функции. Этим будет образован лямбда-вызов:
((nlambda (X1 X2 ... XN) FN) A1 A2 ... AN)
Здесь Ai (i=1,2,...,N) - выражения языка LISP, определяющие фактические параметры.
Вычисление nlambda-вызова производится следующим образом. Сначала формальные параметры связываются с соответствующими фактическими параметрами. Затем с учетом образованных связей вычисляется тело лямбда-выражения, и полученное значение возвращается в качестве результата лямбда-вызова. Формальным параметрам после окончания вычисления возвращаются те связи, которые у них были перед вычислением лямбда-вызова.
Если вычислять значения аргументов функции не нужно, то такую функцию следует определить с помощью nlambda -выражения. Например:
((nlambda (X) (Cdr X)) (1 (* 1 2) 4)) --> ((* 1 2) 4))
((nlambda (X) (Car X)) ((* 1 2) (+ 1 4))) --> (* 1 2)
(list ((nlambda (X) (Car X)) (+ *)) 2 3) --> (+ 2 3)
nlambda –выражения могут служить для создания невычислимых функций и не всегда работают в режиме безымянной функции. С помощью невычисляющих функций (их можно назвать псевдомакросами) легко осуществляется определение новых синтаксических форм. Это необходимо, например, при добавлении в язык новых структур управления, типов данных или при реализации интерпретатора для нового проблемно-ориентированного языка. В частности, использование невычисляющих функций облегчает построение языка с лиспоподобной структурой, имеющего синтаксис, более удобный для пользователя. Однако чрезмерное использование невычисляющих функций затрудняет чтение и понимание программ.
2.7.3. Поименованные функции
С помощью аппарата лямбда-выражений в языке LISP можно определить поименованные функции. Для этой цели необходим конструктор функций, осуществляющий связывание атома (имени функции) с лямбда-выражением. Результат связывания называется lambda - или nlambda -определением функции. В качестве таких конструкторов выступают putd и defun.
2.7.3.1. Функции putd, getd и movd.
Функция putd, имеющая два аргумента, связывает атом, являющийся первым аргументом с lambda - или nlambda -выражением, выступающим в качестве второго аргумента, и возвращает в качестве своего значения имя определяемой функции. Например:
$ (putd F (lambda (X Y) (Cons X Y)))
F
Теперь, определив новую функцию F, мы можем обращаться к ней так:
$ (F 'A '(B))
(A B)
Основным назначением функции putd является, конечно, не возвращение имени, а связывание его с определением функции.
Для доступа к lambda - или nlambda-определениям предназначена функция getd одного аргумента (имя функции), которая возвращает лямбда-определение данной функции. Например:
$ (getd F)
(lambda (X Y) (cons X Y))
Если F есть функция, определенная пользователем, то обращение (getd F) декомпилирует и возвращает определение символа F в виде списка.
Если F является простой функцией или специальной формой, то обращение (getd F) возвращает адрес в физической памяти шаблона функции на машинном языке.
Если F не является специальной формой или функцией, то обращение (getd F) возвращает Nil.
Обращение (getd F flag) возвращает характеристику символа F:
special, если F является специальной формой,
lambda, если F является вычисляемой функцией,
nlambda, если F является невычисляемой функцией,
macro, если F является макро-функцией,
nil, если F неопределен.
Функция (putd F S) компилирует определение S в D-код (специвльное представление для хранения определений функций), при этом модифицирует старое определение функции F и возвращает F. Например:
$ (putd 'Square '(lambda (N) (* N N)))
Square
$ (Square 5)
Функция Movd присваивает функциональное значение, связанное с первым атомом, второму атому. Например:
$ (movd F B)
(lambda (X Y) (cons X Y))
$ (getd B)
(lambda (X Y) (cons X Y))
Функцию movd можно использовать для присваивания других мнемонических имен некоторым функциям LISP без ущерба для эффективности их выполнения.
$ (movd 'car 'First)
First
$ (movd 'cdr 'Rest)
Rest
$ (movd 'cadr 'Second)
Second
$ (movd 'caddr 'Third)
Third
$ (movd 'cadddr 'Fourth)
Fourth
$ (First '(A B C D))
A
2.7.3.2. Функция defun
Для определения новых функций в языке LISP предназначена функция defun. Функция имеет несколько синтаксических форматов. В основном своем формате она имеет три аргумента: первый - имя определяемой функции, второй - список формальных параметров, третий - выражение определяющее значение функции. Своим значением defun возвращает имя определяемой функции:
Например, функцию вычисления факториала
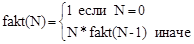
можно определить следующим образом:
$(defun fakt (N) (if (= N 0) 1 (* N (fakt (- N 1)))))
Fakt
Как и в случае с функцией setqи putd возвращаемое значение функции defun не является главным в ее использовании. Основным является побочный эффект функции defun: она заносит во внутренний словарь имя новой функции и связывает его с правилом вычисления возвращаемого значения.
Данное определение эквивалентно следующему:
$ (putd 'fakt '(lambda(N) (if (= N 0) 1 (* N (fakt (- N 1))))))
Fakt
Приведенное определение факториала подразумевает, что аргумент всегда будет целым положительным числом. Можно переопределить функцию таким образом, чтобы для некорректных значений аргумента она возвращала значение nil:
(defun fakt (N)(if (< N 0) nil
(if (= N 0) 1
(* N (fakt (- N 1)))
)
)
)
или
(defun fakt (N)(cond ((< N 0) nil)
((= N 0) 1)
(T (* N (fakt (- N 1))))
)
)
Приведем примеры применения функции defun. Определим функцию atoms, подсчитывающую число атомов в своём аргументе. Функция будет работать следующим образом: Если аргументом является список U, то число атомов равно сумме числа атомов в (car U) и (cdr U). Так как число атомов в каждом из слагаемых меньше, чем в исходном списке, при каждом новом обращении мы будем обрабатывать всё более и более короткие списки и, наконец, придём к случаю, когда аргумент либо пустой список, либо атом. Значением функции atoms при этом должно быть 0 или 1, соответственно. Мы сформулировали сходящуюся рекурсивную процедуру и условие выхода из неё:
(defun atoms (U)(cond ((null U) 0)
((atom U) 1)
(T (+ (atoms (car U)) (atoms (cdr U))))
)
)
(atoms '(A B C)) --> 3
(atoms '(17 217 (13 4) 22)) --> 5
(atoms '()) --> 0
Определим функцию append1 эквивалентную встроенной функции append:
(defun append1 (L1 L2)(if (null L1) L2
(cons (car L1) (append1 (cdr L1) L2)))
)
Встроенная функция reverse инвертирует список. Напишем собственную функцию reverse1, которая будет инвертировать список и все его подсписки любого уровня вложенности:
(defun reverse1 (L)(if (atom L) L
(append (reverse1 (cdr L)) (list (reverse1 (car L))))
)
)
(reverse1 '(A B C D E)) --> (E D C B A)
(reverse1 '(A B ((C D) E))) --> ((E (D C)) B A)
Приведенные примеры определения функций atoms, reverse1 и append1 демонстрируют типичный метод реализации функций обработки списков: при помощи car и cdr список разбивается на две части и каждая из них обрабатывается отдельно (при этом почти всегда используется рекурсивный вызов определяемой функции) и полученные результаты объединяются в конечный ответ.
Рассмотрим еще один метод, часто используемый в функциональном программировании. Вернемся к определению функции reverse1: отдельные элементы списка, являющегося конечным результатом, «накапливаются» на стеке при рекурсивном вызове функции. Когда мы добираемся до самого глубокого уровня вложенности функций, начинается возврат из последовательности вызовов и элементы списка снимаются со стека и собираются в конечный результат (конкретные детали могут зависеть от реализации языка, но суть не изменится). Введем явно объект, накапливающий отдельные элементы результирующего списка: определим функцию rev с двумя аргументами - списками, второй из них будет последовательно получать элементы первого и присоединять к себе в обратном порядке:
(defun rev (L1 L2)
(if (null L1) L2 (rev (cdr L1) (cons (car L1) L2)))
)
Теперь можно определить функцию reverse2 аналогичную reverse1:
(defun reverse2 (L) (rev L nil))
Такой метод носит название «метод накапливающего параметра». Этот метод может привести к существенному повышению эффективности вычислительного процесса. Вернемся к определению функции reverse1 и подсчитаем, сколько раз вызывается основная функция построения списков cons. В случае обращения линейного списка (без подсписков) состоящего из N элементов функция reverse1 вызывает себя рекурсивно N раз; N раз будет вычисляться выражение (list (reverse1 (car L))) эквивалентное (cons (car L) nil) для случая линейного списка. Кроме того, функция reverse1 делает N вызовов функции append, для каждого из этих вызовов append длина первого ее аргумента равна соответственно 1, 2, ..., N-1 и ровно столько раз append будет обращаться к функции cons (см. определение append1). Таким образом, количество вызовов cons функцией append составит
1 + 2 + ... + (N-1) = N*(N-1)/2
Общее количество вызовов cons в функции reverse1 составит
N + N*(N-1)/2 = N*(N+1)/2
В случае использования «метода накапливающего параметра» (функция reverse2) cons будет вызываться функцией rev ровно N раз. Итак, «метод накапливающего параметра» дает существенную экономию вычислений.
Правда, функция reverse2 менее мощная, она обращает только линейные списки. Для обращения вложенных списков можно видоизменить определения функций следующим образом:
(defun rev1 (L1 L2)
(if (null L1) L2 (rev (cdr L1)(cons (list (reverse3(car L1))) L2)))
)
(defun reverse3 (L) (rev L nil))
Рассмотрим еще один пример - сортировки списка, составленного из числовых элементов. Вначале определим функцию insert, которая имеет два аргумента: числовой атом X и упорядоченный список L, а своим значением возвращает упорядоченный список построенный из исходных списка и числа:
(defun insert (X L)(cond((null L) (list X))
((<= X (car L)) (cons X L))
(T (cons (car L) (insert X (cdr L))))
)
)
Теперь определим функцию sort1, которая берет элементы неупорядоченного списка L1 и добавляет их в упорядоченный список L2:
(defun sort1 (L1 L2)(if (null L1) L2
(sort1 (cdr L1) (insert (car L1) L2))
)
)
и, наконец, определим функцию сортировки sort-ins; действие которой сводится к вызову функции sort1 с пустым списком в качестве второго аргумента:
(defun sort-ins (L) (sort1 L nil))
В другом формате функция defunпохожа на функцию Putd, с той лишь разницей, что своих аргументов она не вычисляет. В этом формате функция имеет два аргумента. Первый – имя определяемой функции, второй – лямбда-выражение, определяющее список формальных параметров и тело определяемой функции. Например, следующие определения эквивалентны.
(defun fakt (N) (if (= N 0) 1 (* N (fakt (- N 1))))) <==>
(defun fakt (lambda(N) (if (= N 0) 1 (* N (fakt (- N 1))))))
С помощью –формы можно определять невычисляющие функции.
(defun nl1 (nlambda (X) (Car X)))
$ (nl1 ((* 1 2) (+ 1 4))) --> (* 1 2)
Дата: 2016-10-02, просмотров: 353.