Определение функции (Definitions) в FP выглядит следующим образом
Def l º r
Здесь l имя функции, r –функциональная форма, возможно зависящая от l. Например, определения
Def last1 º l o reverse
Def last º null o tl ® l; last o tl
определяют функцию, выдающую последний элемент последовательности (списка).
Рассмотрим последовательность выполнения функции last на примере last:<l,2> =
-используется определение функции last Þ
=(null o tl ® 1; last o tl):<l,2>=
-исполнение формы (p®f;g) null o tl:<l,2> = null:<2>=F Þ
=last o tl:<l,2>=
-исполнение формы f o g Þ=last:(tl:<l,2>)=
-используется определение функции tail Þ=last:<2>=
-используется определение функции last Þ
=(null o tl ® l; last o tl):<2>=
-исполнение формы (p®f;g) nutl o tl:<2> = null: Æ = T Þ=1:<2>=
-используется определение функции 1 Þ=2.
3.7.5. Семантика
Из вышеизложенного ясно, что система FP определяется выбором следующих множеств.
(a) Множество атомов A (определяющее множество объектов).
(b) Множество примитивных функций P.
(c) Множество функциональных форм F.
(d) Правильно сформированное множество определений D.
Чтобы определить семантику FP, нужно определить правила вычисленияf:xдля всевозможных f и объектов x. Имеется четыре возможности для f:
(l) f примитивная функция; в этом случае в системе имеется ее описание и системе известно, как эта функция применяется;
(2) f функциональная форма; в этом случае описание формы f управляет вычислением f: x;
(3) имеется единственное определение D, вида Def f º r; в этом случае f: x вычисляется как r:x;
(4) ни один из трех вышеперечисленных вариантов; в этом случае f: x=^.
Применение этих правил не гарантирует, что вычислительная процедура будет закончена (не зациклится).
Ограничения FP системы.
Невозможно вычислить программу в рамках FP, т.к. функция не является объектом. По этой же причине FP не может иметь такую функцию, как apply: <x,y> = x :y,(в левой части x- есть объект, а в правой - функция).Также невозможно определить новую функциональную форму. Эти ограничения устраняются в рамках FFP (formal functional programming), которое в данном пособии не рассматривается (см. [21]).
Примеры функциональных программ.
В отличии от программ традиционного стиля, в которых описывается алгоритм получения результата, функциональный стиль программирования предполагает получение функции, которая примененная к входному аргументу даст результат.
Факториал
Def ! º eq0®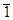 
; * o [id, ! o subl],
Где
Def eq0 º eq o [id,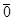 
],
Def subl º - o [id, ].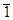
Пример вычисления !:2:
!:2 = (eq0® 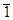;*o[id,! o subl]):2=(*o[id,! o subl):2=(*:[id: 2, ! o subl:2):2= *:<2, !:1> = *:<2, *:<1, !:0>>= *:<2, *:<1, 1>> = *:<2, 1>=2
В данном фрагменте выполнены тождественные преобразования функциональных выражений, аналогичные тем, что выполнялись в разделе 3.7.4 и в начале раздела 3.7, но без дополнительных комментариев.
Скалярное произведение векторов
Определение функции скалярного произведения и ее работа были подробно разобраны выше.
Def IP - (/+)o(@*)oTrans.
Матричное умножение
Матрица представляется в виде списка ее строк
x =< x 1,...,x n> xi =< x i1, ..., x im>
Def MM = (@@IP) o (@distl) o distr o [1, trans o 2]
3.7.7. Элементы алгебры программ
Вычисляя функциональные выражения, мы интуитивно использовали некоторые формулы тождественных преобразований, связывающие различные элементы системы. Эти формулы существуют и их можно выписать в явном виде. Например, докажем, что выполняется отношение: [f,g] o h º [f o h, g o h]
Знак º означает, что программы слева и справа от него представляют собой одно и то же. Данное равенство означает, что для любых функций f, g, и h и любого объекта x, выполняется равенство:
([f,g] o h):x = [f o h, g o h]:x.
Докажем это по уже знакомой схеме:
([f,g] o h):x = [f,g]:(h :x) - по определению композиции;
= <f:(h:x), g:(h:x)> - по определению формы конструирования;
= <(f o h):x, (g o h):x> - по определению композиции;
= [f o h, g o h]:x - по определению формы конструирования/
Некоторые формулы справедливы не для всех объектов. Например,
1 o [f,g] º f не выполняется для объектов x таких, что g:x =^.
Будем писать defined o g ®® 1 o [f,g] º f, чтобы отметить, что формула в правой части верна только для тех объектов x, для которых defined o g:x = T. Здесь
Def defined º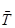 
:
т.е. defined:x º x=^® ^; T.
В общем случае будем писать: p®® f º g, чтобы обозначить, что для всех x, таких, что p:x = T, справедливо f:x=g:x.
Определение.Будем говорить, что f£g если для всех объектов x, либо f:x = ^, либо f:x = g:x.
Определение.Будем говорить, что f º gеслиf£gи g£f.
£ есть частичный порядок на множестве функций, f£g означает, что g – есть расширениеf.
3.7.7.1. Основные тождества
Основные принципы и приемы доказательств приведены в предыдущих разделах. Предлагается доказать следующие тождества в качестве упражнений.
1.Композиция и конструирование
1.1 [fl,...,fn] o g º [fl o g,...,fn o g]
1.2 @f o [gl,...,gn] º [f o gl,...,f o gn]
1.3 /f o [gl,...,gn] º f o [ gl , //f ol [g2,...,gn]]при n³2
º f o [gl, f o [g2,...,f o [gn-1, gn]…]]
//f o [g] º g
1.4 f o [ 
,g] º (bu f x) o g
1.5 1 o [fl,...,fn] £ fl
s o [fl,...,fs,...,fn] £ fs для s£n
defmed o fi (для всех i¹s, l£i£n) ®® s o [fl,...,fsl,...,fn] º fs
1.5.1 [fl o 1,...,fn o n] o [gl,...,gn] º [fl o gl,...,fn o gn]
1.6 tl o [fl] £ Æ;
tl o [fl,...,fn] £[f2,...,fn] для n³2
defmed o fl ®® tl o [fl] º Æ
и tl o [fl,...,fn] º [f2,...,fn] для n³2
1.7 distl o [f, [gl,...,gn]] º [[f, gl],...,[f, gn]]
defmed o f®® distl o [f,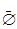 
] º ]]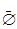
1.8 apndl o [f, [gl,...,gn]] º [f,gl,...,gn]
null o g®® apndl o [f,g] º [f]
1.9 [...,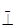 
,...] º ,
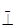1.10 apndl o [f o g, @f o h] º @f o apndl o [g,h]
I.l1 pair & not o null o l ®® apndl o [[1 o 1,2], distr o [tl o 1,2]] º distr, где f&g º and o [f,g];
pair º atom ® F; eq o [length,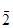 
]
II Композиция и условное
II.l (p®f; g) o h º p o h ® f o h; g o h
II.2 h o (p® f; g) º p ® h o f; h o g
II.3 or o [q,not o q]®® and o [p,q]® f; and o [p,not o q]® g;
h º p® (q®f; g); h
II.3.1 p ® (p® f; g); h º p® f; h
III Композиция и разное
III.1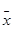 
o f_£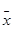
defined o f_®® 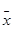o f_º ,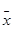
III.l.l 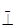o f º f 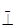o º ,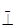
III.2 f o id º id o f º f
III.3 pair®® l o distr º [l o l,2],
pair ®® l o tl º 2.
IlI.4 @ (f o g) º @f o @g
III.5 null o g®® @fog º ]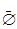
IV Условное и конструирование
IV.l [fl,...,(p®g;h),...,fn] º p® [fl,...,g,...,fn]; [fl,...,h,...,fn]
IV.l.1 [fl,..., (pl ® gl; ... ;pn ® gn; h) ,...,fn] º pl ® [fl,..., gl ,...,fn];…pn ® [fl,..., gn,...,fn]; [fl,..., h,...,fn]
3.7.7.2. Задачи на доказательство
Рассмотрим доказательства некоторых более сложных формул алгебры программ.
Задача 1.apndl o [f o g, @f o h] º @f o apndl o [g,h]
Доказательство:
1.h:xне является ни пустым, ни непустым списком
Тогда обе части обращаются в ^ после применения к x.
2. h:x = Æ. Тогда
apndl o [f o g, @f o h]: x º apndl: <f o g:x, Æ> º <f:(g:x)>
@f o apndl o [g,h]: x º @f o apndl: <g:x, Æ> º @f:<g:x>º <f:(g:x)>
3.h:x = <yl ,...,yn>. Тогда
apndl o [f o g, @f o h]: x º apndl: <f o g:x, @f: <yl ,...,yn>> º <f:(g:x),f:yl,...,f:yn>
@f o apndl o [g,h]: x º @f o apndl: <g:x, <yl ,...,yn>> º @f:<g:x,yl ,...,yn >º <f:(g:x),f:yl,...,f:yn>
Задача 2.
pair & not o null o l ®® apndl o [[1 o 1,2], distr o [tl o 1,2]] º distr,
где f&g º and o [f,g];
pair º atom ® F; eq o [length, 
]
Доказательство:
1. x атом или ^. Тогда distr: <x,y> = ^. Левая часть также обращается в ^ после применения к <x,y>, tl o 1 :<x,y> = ^ и т.д..
2. x = < xl ,..., xn>. Тогда
apndl o [[1 o 1,2], distr o [tl o 1,2]]:<x, y>º apndl: <<l:x, y>, distr: <tl:x, y>>º apndl: <<xl,y>, Æ> = <<xl,y>>, если tl:x = Æ
apndl: <<xl,y>, <<x2,y>,..., <xn,y>>>, еслиtl:x ¹ Æ
º <<xl ,y>, ... , <xn,y>>º distr: <x,y>
Дата: 2016-10-02, просмотров: 258.
