ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Математическое обеспечение
Автоматизированных систем управления»
С.А.Cавушкин
ФУНКЦИОНАЛЬНОЕ ПРОГРАММИРОВАНИЕ
Учебное пособие по курсам
«Функциональное программирование» и «Функциональное и логическое программирование»
Москва – 2012
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Математическое обеспечение
Автоматизированных систем управления»
С.А.Cавушкин
ФУНКЦИОНАЛЬНОЕ ПРОГРАММИРОВАНИЕ
Рекомендовано редакционно-издательским советом
университета в качестве учебного пособия для студентов, обучающихся по направлению 230100 «Информатика и вычислительная техника», профиль «Программное обеспечение вычислительной техники и автоматизированных систем», а также по направлению 231000 «Программная инженерия»
Москва – 2012
УДК 004
С 12
Cавушкин С.А. Функциональное программирование. Учебное пособие для студентов, обучающихся по направлению 230100 «Информатика и вычислительная техника», профиль «Программное обеспечение вычислительной техники и автоматизированных систем», а также по направлению 231000 «Программная инженерия». - М.: МИИТ, 2012. - 141 с.
В учебном пособии излагаются сведения по теории функционального программирования, в частности элементы лямбда-исчисления и алгебры комбинаторов, которые лежат в основе функционального программирования, приведена модель Бэкуса. Описаны синтаксис и семантика, а также основные приемы и примеры программирования на языках LISP и HASKELL. Сформулированы варианты заданий и методические указания для выполнения лабораторных работ.
Учебное пособие предназначено для студентов, обучающихся по направлению 230100 «Информатика и вычислительная техника», профиль «Программное обеспечение вычислительной техники и автоматизированных систем», а также по направлению 231000 «Программная инженерия»
Рецензенты:
зав. кафедрой ВСС МИИТа к. т. н., доцент В. Н. Нагинаев;
профессор Российской международной академии туризма,
к.т.н В. Г. Шапошников
© МИИТ, 2012
СОДЕРЖАНИЕ
1. Парадигмы программирования.. 7
2. Лисп (LISP) – как язык функционального программирования 9
2.1. Атомы и списки. Функции. 10
2.2. Функции работы со списками. 13
2.3. Основные функции. 15
2.4. Функции ввода/вывода. 17
2.5. Другие функции. 20
2.6. Порядок вычислений в LISP'е. 22
2.7. Определение новых функций. 26
2.7.1. Безымянные вычисляемые функции. 26
2.7.2. Невычисляющие функции. 27
2.7.3. Поименованные функции. 29
2.7.4. Функции с нефиксированным числом аргументов. 36
2.7.5. Фунарг-проблема. Замыкание. 36
2.8. Функции высших порядков. Функционалы. 39
2.9. Макросы.. 48
3. Теоретические основы функционального программирования 51
3.1. Функции, функциональные выражения. 51
3.2. Рекурсивные определения функции. 52
3.3. Функции высших порядков, функционалы.. 55
3.4. Исчисление функциональных типов. 57
3.4.1. Параметрический тип и полиморфизм.. 58
3.5. Карринг. 59
3.6. λ-исчисления и алгебра комбинаторов. 61
3.6.1. λ–термы.. 61
3.6.2. Подстановки. 62
3.6.3. Конверсии. 62
3.6.4. Неподвижная точка. 63
3.6.5. Редукции. 63
3.6.6. Нормальная форма λ-термов. 66
3.6.7. Стратегии применения редукций. Аппликативный и нормальный порядок редукций 67
3.6.8. Алгебра комбинаторов. 68
3.7. Функциональный язык Бэкуса. 71
3.7.1. Состав системы FP. 72
3.7.2. Функции FP. 73
3.7.3. Функциональные формы.. 75
3.7.4. Определение пользовательских функций. 77
3.7.5. Семантика. 77
3.7.6. Примеры функциональных программ. 78
3.7.7. Элементы алгебры программ.. 79
4. HASKELL – язык функционального программирования.. 83
4.1. Типы.. 83
4.1.1. Основные типы.. 83
4.1.2. Арифметика. 84
4.1.3. Кортежи. 85
4.1.4. Списки. 86
4.1.5. Строки. 87
4.2. Определение функций. 88
4.2.1. Условные выражения. 90
4.2.2. Функции многих переменных и порядок определения функций. 91
4.2.3. Операция выбора и правила выравнивания. 91
4.2.4. Кусочное задание функций. 92
4.2.5. Сопоставление с образцом.. 92
4.2.6. let-связывание. 94
4.2.7. Охраняющие условия. 96
4.2.8. Полиморфизм.. 97
4.3. Пользовательские типы.. 97
4.3.1. Синонимы типов. 98
4.3.2. Пары.. 98
4.3.3. Множественные конструкторы.. 99
4.3.4. Классы типов. 101
4.4. Рекурсивные типы.. 102
4.4.1. Списки как рекурсивные типы.. 103
4.4.2. Синтаксические деревья. 104
4.5. Функции высшего порядка. 106
4.5.1. λ–абстракции. 109
4.6. Определение операторов. 110
4.6.1. Секции. 111
4.7. Модули. 111
4.8. Абстрактные типы данных. 112
4.9. Операции ввода-вывода. 114
4.9.1. Базовые операции ввода-вывода. 114
4.9.2. Стандартные операции ввода-вывода. 115
4.10. Создание исполняемых программ.. 117
4.11. Монады.. 117
4.11.1. Последовательные вычисления (монада IO) 117
4.11.2. Вычисления с обработкой отсутствующих значений (монада Maybe) 118
4.11.3. Вычисления с несколькими результатами (монада List) 119
4.11.4. Операции «>>=» и return. 121
4.11.5. Законы монад. 122
4.11.6. Стандартные монады.. 123
5. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНОЙ РАБОТЫ ПО ЛОГИЧЕСКОМУ ПРОГРАММИРОВАНИЮ... 126
5.1. ЗАДАНИЕ N1. Работа со списками (на LISP’е и HASKELL’е) 126
5.1.1. Методические указания. 126
5.1.2. Варианты.. 127
5.2. ЗАДАНИЕ N2. Графы и деревья (на LISP’е и HASKELL’е) 130
5.2.1. Методические указания. 130
5.2.2. Варианты.. 130
5.3. ЗАДАНИЕ N3. Разные задачи (на LISP’е и HASKELL’е) 135
5.3.1. Методические указания. 135
5.3.2. Варианты.. 135
5.4. Упражнения. 137
5.5. Содержание отчета. 138
Парадигмы программирования
Парадигма (от греч. παράδειγμα, «пример, модель, образец») — осмысление мира на основе идей, взглядов и понятий. Современное значение этого термина в философии науки используется для обозначения исходной концептуальной схемы, модели постановки проблем и их решения, методов исследования.
Под парадигмой программирования будем понимать систему взгляд, подходов, позиций, определяющую стиль программирования на концептуальном уровне. Парадигма программирования представляет (и определяет) то, как программист видит процесс выполнения программы и, в конечном счете, саму программу.
В литературе формулируется большое число парадигм программирования. Мы выделим следующие:
Императивное программирование — процесс вычисления описывается в виде последовательности команд, изменяющих состояние вычислительной среды. Этот стиль программирования является традиционным и связывается с именем фон Неймана, который разработал основные архитектурно-функциональные принципы построения вычислительных машин (управления выполнением программы, хранимой в памяти программы, счетчик команд), которые легли в основу понятия фон-Неймановской архитектуры вычислительных устройств и фон-Неймановского стиля программирования.
Процедурное программирование — часто используется как синоним императивного программирования. При этом команды реализуются вызовами процедур.
Объектно-ориентированное программирование — программа – это набор взаимодействующих объектов. Каждый объект обладает набором свойств, а также набором методов - программ, которые связывают значения свойств данного объекта и других объектов друг с другом.
Функциональное программирование — программа представляется в виде композиции и суперпозиции функций. Программы не представляют собой последовательности инструкций и не имеют глобального состояния.
Логическое программирование — программа обычно определяет, что надо вычислить, а не то, как это надо делать. Выполнение программы основано на выводе новых утверждений из набора исходных утверждений, согласно заданным логическим правилам вывода.
Структурное программирование — в настоящее время общепринятая методология, в основе которой лежит представление программы в виде иерархии структур управления (последовательное исполнение операций, ветвление в зависимости от выполнения некоторого заданного условия, цикл, вызов подпрограмм). Разработка программы ведётся пошагово, методом «сверху вниз». Исторически возникло из традиционного императивного программирования путем ограничения применения «неструктурных» операторов, таких как оператор GOTO (безусловного перехода). Использование произвольных переходов в тексте программы приводило к получению запутанных, программ, по тексту которых практически невозможно понять порядок исполнения и взаимозависимость фрагментов.
Программа, управляемая данными — программа представляется в виде графа с вершинами двух видов – процедуры и данные. Данные могут быть входами и выходами процедур. Программа запускается посредством запроса вида «ДАНО-НАЙТИ».
Из выбранных парадигм нас интересуют императивное программирование и его разновидности, как представляющие традиционный стиль программирования, а также функциональное программирование, которое является темой данного пособия. Остальные парадигмы приведены в качестве примеров.
Input
(+ 2 3)
Функция read совместно с другими функциями позволяют читать выражения внешние по отношению к программе. Из них можно строить новые выражения или новые программы.
Функция print выводит в файл, уже выбранный для вывода вычисленное значение аргумента и символ «перевод строки». Например:
$ (print "Вывод текста на экран!")
Вывод текста на экран!
Как и функция read,print является псевдофункцией, у которой есть как побочный эффект, так и значение. Значением функции является значение ее аргумента, а побочным эффектом - печать этого значения.
Отметим, что функции ввода-вывода очень гибки, поскольку их можно использовать в качестве аргументов других функций. Например:
(+ (print 2) 3)
Если мы используем print на самом верхнем уровне, S-выражение печатается дважды. Причиной этого служит то, что функция print (так же, как и read в подобной ситуации) не только используется для своего действия (печати), но, кроме того, имеет и значение (этим значением служит значение ее аргумента), которое также печатается.
Например,
(setq x '(1 2 3))
(1 2 3)
(print x)
(1 2 3)
(1 2 3)
Функция print часто используется временно внутри программы для печати промежуточных результатов в процессе отладки программы.
Функция prin1 выводит в файл, уже выбранный для вывода значение аргумента без последующего перевода строки. Таким образом, функция prin1 действует так же, как и функция print, но в файл вывода не выводится символ «перевод строки». Например:
(setq x '(1 2 3))
(1 2 3)
(prin1 x)
(1 2 3)(1 2 3)
Как функцией print, так и функцией prin1 можно выводить кроме атомов и списков и другие типы данных, например, строки:
(prin1 "a b c")
A b ca b c
Вывод выражений часто желательно разбить на несколько строк. Перевод строки можно осуществить функцией terpri (TERminate PRInting). У функции terpri нет аргументов и в качестве значения она возвращает nil. Например:
(progn (prin1 a) (terpri) (print b) (prin1 c))
a
b
cc
Функция prognреализует возможности фон-Неймановского стиля программирования в LISPе. Она последовательно вычисляет значения своих аргументов, список которых рассматривается как последовательность команд. При этом функция реагирует на специальные конструкции, которые управляют переходами, разветвлениями , циклами. Данная функция не вписывается в функциональный стиль программирования и, поэтому здесь подробно не рассматривается[1].
Функцию print можно определить с помощью terpri и prin1 следующим образом: (progn (prin1 x) (terpri))
Функция spaces выводит в файл, уже выбранный для вывода указанное количество символов «пробел» и возвращает их количество. Например:
$(spaces 11)
………..11
2.5. Другие функции
В языке LISP имеется большое количество различных встроенных функций. В этом разделе мы рассмотрим лишь некоторые из них, пояснения относительно других - будем давать в следующих разделах по мере необходимости.
Функция setq применяется для связывания атома, она имеет два аргумента: первый - имя атома, второй - произвольное выражение. В результате выполнения функции setq указанный атом принимает значение равное вычисленному значению второго аргумента:
(setq A 23) A --> 23
(setq B (list A 35)) B --> (23 35)
В качестве своего значения функция setq возвращает значения второго аргумента. Следовательно, возможно «ступенчатое» использование функции:
(setq X (cons C (setq Y (list D E)))) Y --> (D E) X --> (C D E)
Функция set также применяется для связывания атома, в отличие от setq первый аргумент в качестве значения должен выдать имя атома, второй, как и для setq - произвольное выражение. В результате выполнения функции set атом-значение первого аргумента принимает значение вычисленного второго аргумента:
(setq A 'B) A --> B
(set A 35) B --> 35
Для setq и set основным результатом является не возвращаемое значение, а побочный эффект - связывание атома. Таким образом, она является типичным примером псевдофункции (другой пример псевдофункций: рассмотренные выше функции read и print). Имеется множество других примеров функций с побочными эффектами. С подобными функциями всегда следует обращаться осторожно, т.к. побочные эффекты могут привести к непредсказуемым результатам и нарушают строго функциональный подход[2].
Логические функции not, and и or выполняют операции отрицания, конъюнкции и дизъюнкции:
(not T) --> nil
(and T nil) --> nil
(or T nil) --> T
В большинстве версий языка LISP функции and и or определены как функции от нескольких аргументов и реализованы как «ленивые» функции. Кроме того, при использовании логических функций следует помнить, что логическое значение «ложь» в LISP’е обозначается тем же атомом, что и пустой список (nil), а «истиной» считается, кроме атома T – любое значение, не являющееся nil. Если очередной аргумент функции and имеет значение nil, то последующие аргументы не вычисляется, значением функции считается nil,если все аргументы функции andвычислены и ни один из них не имеет значения nil, то значением функции and считается значение последнего аргумента. Аналогично для функции or: если очередной аргумент имеет значение T (не nil) - не вычисляется второй аргумент. Например:
(or '() 12345)
(or '(1 2 3) 12345)
(1 2 3)
(and '(1 2 3) (setq x 1))
(and '() (setq y 2))
Nil
Это свойство позволяет использовать функции для организации выполнения последовательности действий. В приведенном примере, учитывая, что функция terpri вырабатывает значение nil,используется конструкция (not (terpri)):
(and (prin1 a) (not (terpri)) (print b) (prin1 c))
a
b
cc
Для объединения двух списков предназначена функция append, она имеет два аргумента - оба должны быть списками, в результате своего действия она соединяет эти два списка в один:
(append (list 1 2 3) (list a b c)) --> (1 2 3 a b c)
Следует различать действия функций cons и append, так например:
(append (list a b) (list c d)) --> (a b c d),
но (cons (list a b) (list c d)) --> ((a b) c d).
Это два разных списка, первый из них - список из четырех элементов - (a b c d), второй - список из трех элементов - ((a b) c d), причем первый элемент сам является списком - (a b).
В языке LISP имеется множество других функций для обработки списков и других целей, например, функция reverse - инвертирующая список: (reverse (list 1 2 3)) --> (3 2 1), функция length - определяющая количество элементов в списке: (length (list a b c)) --> 3и т. д. Практически все они могут быть определены через основные.
2.6. Порядок вычислений в LISP'е
Любое допустимое LISP-выражение вычисляется в ходе обработки интерпретатором языка LISP. Вычисления проводится по-разному для атома и списка.
Вычисление атома заключается в использовании его значения, установленного в процессе связывания атома. Значением атома может быть другой атом, список или функция. Вычисление атома производится независимо от того, одиночный это атом, является ли он элементом списка, т.е. аргументом функции. Например:
(setq A B) A --> B
(setq B C) B --> C
(setq D B) D --> C
в результате первого присваивания атом A получит значение B (в этот момент атом B не связан с другим значением, его значением является он сам) и, аналогично, при втором присваивании атом B получает значение C. В третьем случае, при исполнении функции setq будет вычислено значение атома B (в данном случае C) и атом D будет связан с полученным значением. При последующих вычислениях атомов A и D будут использованы их значения B и C соответственно:
(setq E A) E --> B
(setq F D) F --> C
В результате проведенных операций атом A имеет своим значением B, а атом B, в свою очередь, C. При вычислении значения атома интерпретатор языка LISP использует лишь один уровень связи значений. В операции (setq X A) используется связь A-->B и игнорируется следующий уровень B-->C. Для принудительного вычисления различных уровней связи значений предназначена функция eval. При вызове функции eval (как и любой другой функции языка LISP) вычисляется значение ее аргумента, а значением функции eval будет значение от полученного результата. Иными словами, значением функции eval будет значение значения ее аргумента. Приведём ещё один пример:
(setq X Y) X --> Y
(setq Y Z)
(eval X) --> Z
(setq Z T)
(eval (eval X)) --> T
Предотвратить или отменить вычисление выражения (вычисление интерпретатором или функцией eval) можно при помощи функции quote. (quote X) всегда имеет своим значением X, независимо от того, является атом X связанным или свободным. Если действительны последние присвоения для X, Y и Z, действие функции quote можно продемонстрировать на следующих примерах:
X --> Y
(quote X) --> X
(eval X) --> Z
(eval (qoute X)) --> Y
(eval (eval (quote X) --> Z
Функцию отмены вычислений можно использовать для того, чтобы связанный атом сделать свободным:
(setq X (quote X)) X --> X
Как было сказано выше, в языке LISP вызовы функций представлены в виде списков (S-выражений). Первый элемент списка - имя функции, следующие элементы - аргументы функции. Вычисление любого списка сводится к попытке интерпретации его первого элемента как имени функции (при неудаче появляется сообщение об ошибке), а остальных элементов как аргументов этой функции. Попытка задать список непосредственно во входной строке языка окончится неудачей, так как интерпретатор воспримет список как функцию и попытается её вычислить. Для задания не вычисляемого списка можно использовать функцию list, используется также функция quote, отменяющая интерпретацию списка. Однако результаты применения функций list и quote могут быть разными, если элементы, из которых строится список, являются связанными:
(setq A 1)
(setq B 2)
(setq C 3)
(list A B C) --> (1 2 3)
(quote (A B C)) --> (A B C)
Любая функция языка программирования LISP может использовать значение другой функции в качестве своего аргумента, т.е. допускается вложенность или суперпозиция функций. В этом случае интерпретатор языка придерживается «естественного» порядка вычислений: изнутри-наружу[3]. Перед нахождением значения функции любого уровня вложенности вычисляются значения ее аргументов.
(cons (car (list 1 2)) (quote 2 3)) --> (1 2 3)
В приведенном примере перед нахождение значения функции cons вычисляются значения ее аргументов - функции car и quote; исполнение функции car, в свою очередь, приводит к предварительному вычислению функции list и так далее. Функции quote и eval позволяют управлять порядком вычислений: отменять вычисление выражения или проводить повторные вычисления соответственно.
Рассмотренная ранее функция setq «неправильная» функция, так как при ее исполнении не вычисляется значение ее первого аргумента:
(setq X Y) X --> Y
(setq X 1) X --> 1
в последнем случае значение 1 принимает атом X, хотя и является связанным, если бы вычислялось его значение, то значение 1 принял бы атом Y. Более «правильная» функция set - имеет тот же побочный эффект что и setq, но вычисляет значения обоих своих аргументов:
(setq A B) A --> B
(set A 1) A --> B B --> 1
Дело в том, что функция setq более короткая форма записи функции set с отменой вычисления первого аргумента.
(setq A B) <==> (set (quote A) B)
Поскольку функция quote используется довольно часто, для нее используется более лаконичная форма записи:
(quote X) <==> 'X
2.7. Определение новых функций
Программная реализация функционального алгоритма сводится к определению новых собственных функций программиста и, среди них, некоторой основной функции, для которой входные данные играют роль аргументов, а возвращаемое значение - результатом решаемой задачи. Для определения новых функций в языке LISP существует несколько способов. Рассмотрим их по порядку.
Square
$ (Square 5)
Функция Movd присваивает функциональное значение, связанное с первым атомом, второму атому. Например:
$ (movd F B)
(lambda (X Y) (cons X Y))
$ (getd B)
(lambda (X Y) (cons X Y))
Функцию movd можно использовать для присваивания других мнемонических имен некоторым функциям LISP без ущерба для эффективности их выполнения.
$ (movd 'car 'First)
First
$ (movd 'cdr 'Rest)
Rest
$ (movd 'cadr 'Second)
Second
$ (movd 'caddr 'Third)
Third
$ (movd 'cadddr 'Fourth)
Fourth
$ (First '(A B C D))
A
2.7.3.2. Функция defun
Для определения новых функций в языке LISP предназначена функция defun. Функция имеет несколько синтаксических форматов. В основном своем формате она имеет три аргумента: первый - имя определяемой функции, второй - список формальных параметров, третий - выражение определяющее значение функции. Своим значением defun возвращает имя определяемой функции:
Например, функцию вычисления факториала
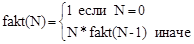
можно определить следующим образом:
$(defun fakt (N) (if (= N 0) 1 (* N (fakt (- N 1)))))
Fakt
Как и в случае с функцией setqи putd возвращаемое значение функции defun не является главным в ее использовании. Основным является побочный эффект функции defun: она заносит во внутренний словарь имя новой функции и связывает его с правилом вычисления возвращаемого значения.
Данное определение эквивалентно следующему:
$ (putd 'fakt '(lambda(N) (if (= N 0) 1 (* N (fakt (- N 1))))))
Fakt
Приведенное определение факториала подразумевает, что аргумент всегда будет целым положительным числом. Можно переопределить функцию таким образом, чтобы для некорректных значений аргумента она возвращала значение nil:
(defun fakt (N)(if (< N 0) nil
(if (= N 0) 1
(* N (fakt (- N 1)))
)
)
)
или
(defun fakt (N)(cond ((< N 0) nil)
((= N 0) 1)
(T (* N (fakt (- N 1))))
)
)
Приведем примеры применения функции defun. Определим функцию atoms, подсчитывающую число атомов в своём аргументе. Функция будет работать следующим образом: Если аргументом является список U, то число атомов равно сумме числа атомов в (car U) и (cdr U). Так как число атомов в каждом из слагаемых меньше, чем в исходном списке, при каждом новом обращении мы будем обрабатывать всё более и более короткие списки и, наконец, придём к случаю, когда аргумент либо пустой список, либо атом. Значением функции atoms при этом должно быть 0 или 1, соответственно. Мы сформулировали сходящуюся рекурсивную процедуру и условие выхода из неё:
(defun atoms (U)(cond ((null U) 0)
((atom U) 1)
(T (+ (atoms (car U)) (atoms (cdr U))))
)
)
(atoms '(A B C)) --> 3
(atoms '(17 217 (13 4) 22)) --> 5
(atoms '()) --> 0
Определим функцию append1 эквивалентную встроенной функции append:
(defun append1 (L1 L2)(if (null L1) L2
(cons (car L1) (append1 (cdr L1) L2)))
)
Встроенная функция reverse инвертирует список. Напишем собственную функцию reverse1, которая будет инвертировать список и все его подсписки любого уровня вложенности:
(defun reverse1 (L)(if (atom L) L
(append (reverse1 (cdr L)) (list (reverse1 (car L))))
)
)
(reverse1 '(A B C D E)) --> (E D C B A)
(reverse1 '(A B ((C D) E))) --> ((E (D C)) B A)
Приведенные примеры определения функций atoms, reverse1 и append1 демонстрируют типичный метод реализации функций обработки списков: при помощи car и cdr список разбивается на две части и каждая из них обрабатывается отдельно (при этом почти всегда используется рекурсивный вызов определяемой функции) и полученные результаты объединяются в конечный ответ.
Рассмотрим еще один метод, часто используемый в функциональном программировании. Вернемся к определению функции reverse1: отдельные элементы списка, являющегося конечным результатом, «накапливаются» на стеке при рекурсивном вызове функции. Когда мы добираемся до самого глубокого уровня вложенности функций, начинается возврат из последовательности вызовов и элементы списка снимаются со стека и собираются в конечный результат (конкретные детали могут зависеть от реализации языка, но суть не изменится). Введем явно объект, накапливающий отдельные элементы результирующего списка: определим функцию rev с двумя аргументами - списками, второй из них будет последовательно получать элементы первого и присоединять к себе в обратном порядке:
(defun rev (L1 L2)
(if (null L1) L2 (rev (cdr L1) (cons (car L1) L2)))
)
Теперь можно определить функцию reverse2 аналогичную reverse1:
(defun reverse2 (L) (rev L nil))
Такой метод носит название «метод накапливающего параметра». Этот метод может привести к существенному повышению эффективности вычислительного процесса. Вернемся к определению функции reverse1 и подсчитаем, сколько раз вызывается основная функция построения списков cons. В случае обращения линейного списка (без подсписков) состоящего из N элементов функция reverse1 вызывает себя рекурсивно N раз; N раз будет вычисляться выражение (list (reverse1 (car L))) эквивалентное (cons (car L) nil) для случая линейного списка. Кроме того, функция reverse1 делает N вызовов функции append, для каждого из этих вызовов append длина первого ее аргумента равна соответственно 1, 2, ..., N-1 и ровно столько раз append будет обращаться к функции cons (см. определение append1). Таким образом, количество вызовов cons функцией append составит
1 + 2 + ... + (N-1) = N*(N-1)/2
Общее количество вызовов cons в функции reverse1 составит
N + N*(N-1)/2 = N*(N+1)/2
В случае использования «метода накапливающего параметра» (функция reverse2) cons будет вызываться функцией rev ровно N раз. Итак, «метод накапливающего параметра» дает существенную экономию вычислений.
Правда, функция reverse2 менее мощная, она обращает только линейные списки. Для обращения вложенных списков можно видоизменить определения функций следующим образом:
(defun rev1 (L1 L2)
(if (null L1) L2 (rev (cdr L1)(cons (list (reverse3(car L1))) L2)))
)
(defun reverse3 (L) (rev L nil))
Рассмотрим еще один пример - сортировки списка, составленного из числовых элементов. Вначале определим функцию insert, которая имеет два аргумента: числовой атом X и упорядоченный список L, а своим значением возвращает упорядоченный список построенный из исходных списка и числа:
(defun insert (X L)(cond((null L) (list X))
((<= X (car L)) (cons X L))
(T (cons (car L) (insert X (cdr L))))
)
)
Теперь определим функцию sort1, которая берет элементы неупорядоченного списка L1 и добавляет их в упорядоченный список L2:
(defun sort1 (L1 L2)(if (null L1) L2
(sort1 (cdr L1) (insert (car L1) L2))
)
)
и, наконец, определим функцию сортировки sort-ins; действие которой сводится к вызову функции sort1 с пустым списком в качестве второго аргумента:
(defun sort-ins (L) (sort1 L nil))
В другом формате функция defunпохожа на функцию Putd, с той лишь разницей, что своих аргументов она не вычисляет. В этом формате функция имеет два аргумента. Первый – имя определяемой функции, второй – лямбда-выражение, определяющее список формальных параметров и тело определяемой функции. Например, следующие определения эквивалентны.
(defun fakt (N) (if (= N 0) 1 (* N (fakt (- N 1))))) <==>
(defun fakt (lambda(N) (if (= N 0) 1 (* N (fakt (- N 1))))))
С помощью –формы можно определять невычисляющие функции.
(defun nl1 (nlambda (X) (Car X)))
$ (nl1 ((* 1 2) (+ 1 4))) --> (* 1 2)
Para1
$ (mapcar Para1 X)
((A 1) (B 1) (C 1))
$ (mapcar numberp (1 2 nonumb 3))
(T T nil T)
Дан список, содержащий целые положительные числа. Построить функцию, возвращающую список, состоящий из факториалов каждого элемента исходного списка.
(defun Demo (lambda (F L)
(prin1 «Результат действия mapcar: «)
(mapcar F L)
))
(defun Fact (X)
(cond ((equal X 0) 1 ) (T (* X (Fact (- X 1))) )
))
Протестируем определения функций.
$ (Demo Fact (2 3 4))
Nil
$ (macroexpand-1 '(push2 d s ) )
(setq s (cons d s))
$ (macroexpand-1 '(my-setq s (a s d)) )
(setq s (quote (a s d))))
Приведем еще один пример. Определим рекурсивный макрос:
(defmacro my-copy-list (x)
(cond ( (null x) nil )
(T (list 'cons (list 'quote (car x))
(list ' my-copy-list (cdr x))
) ) ) )
и обратимся к функции macroexpand-1:
$ (my-copy-list (a s d))
(a s d)
$ (macroexpand-1 '(my-copy-list (a s d)))
(cons (quote a) (my-copy-list (s d)))
Если F есть макровызов, то функция (Macroexpand-1 F)повторно расширяет F до тех пор, пока результат расширения не будет макровызовом.
Примеры.
Функция f(x)=2*x удвоения числа имеет тип f:R ®R
Функция f(x,y)=x+y сложения чисел имеет тип f:RÄ R ®R
здесь R – множество чисел.
Пусть теперь A-алфавит, из которого оставляются строки, A*-множество строк над алфавитом A.
Функция f(x,y)=xy конкатенация символьных строк имеет тип f:A*ÄA*®A*.
Функция f(x)=y взятия головного символа строки имеет тип f:A*®A.
Функция f(x, y)= xy присоединения головного символа к строке имеет тип f: AÄA*®A*.
Пример.
Если имеются функции сравнения, например, < с различными типами одна типа <:R® R, другая - типа <: A*®A* (см. предыдущий пример), то на их основе можно определить программу сортировки, которая будет полиморфной и иметь параметризованный тип sort:X*®X*, где X-параметр, принимающий значения R или A*. При этом X*-может обозначать массив числовой или массив строк символов алфавита A.
Пример.Автоаппликация.
Рассмотрим функцию высшего порядка, рассмотренную выше и известную в программировании под именем map. Ее тип map: (X ®Y)Ä X*®Y*. Если эту функцию преобразовать так, чтобы ее можно было применить только к первому ее аргументу, то ее тип преобразуется в следующий map1:(X®Y)®(X*®Y*). Функция map1 преобразует скалярную функцию, доопределяя ее для векторных (списковых) аргументов.
Аргумент функции map1 имеет тип (X®Y) для различных значений параметров X и Y. Интересно, что сама функция map1 является функцией того же типа map1: X®Y, где X= X ®Y, Y= X*®Y*.
В связи с этим функция map1 применима к самой себе. Такое явление называется самоприменимостью или автоаппликацией.
Какой же тип будет у результата map1(map1). По правилам исчисления функциональных типов map1: (X ®Y) ®(X*®Y*), в то же время map1: X®Y. Значит map1(map1):(X*®Y*), но в данном случае X=X®Y и Y=X*®Y*. Значит, тип результата будет map1(map1):(X®Y)*®(X*®Y*)*. Итак, результатом будет функция, на вход которой подается список скалярных функций, а на выходе получается список аналогичных функций, доопределенных для векторных (списковых) аргументов.
3.5. Карринг
Под каррингом понимается применение функции к неполному списку аргументов. Результатом такого применения является функция от остальных аргументов. Например, если функция add определена как
add x y = x+y,
то можно определить функцию inc, увеличивающую свой аргумент на 1 следующим образом:
inc = add 1
Бинарные инфиксные операции являются функциями двух переменных и, следовательно, для них также допустим карринг. Например, если операция «+» двухместная и имеет тип +:RÄ R ®R, то функция «1+»- одноместная, прибавляет 1 к своему аргументу и имеет тип 1+:R®R
Карринг в узком смысле – это применение функции только к одному, самому первому своему аргументу. Это практически означает, что всякая функция нескольких переменных, имеющая тип f: X1Ä X2Ä...Ä XN®Y, преобразуется к типу f: X1® (X2®...® (XN®Y)...), т. е. всякая функция является функцией только одного аргумента, а результатом может являться другая функция.
Пример.
Функция map1 определена как функции одного аргумента. Тогда
map1(*2) – функция, ум<
Дата: 2016-10-02, просмотров: 317.