Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Эффективными системами криптографической защиты данных являются асимметричные криптосистемы, называемые также криптосистемами с открытым ключом. В таких системах для зашифрования данных используется один ключ, а для расшифрования – другой ключ (отсюда и название – асимметричные). Первый ключ является открытым и может быть опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью открытого ключа невозможно.

Для расшифрования данных получатель зашифрованной информации использует второйключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа зашифрования.

Обобщенная схема асимметричной криптосистемы с открытым ключом показана на рис.2.1. В этой криптосистеме применяют два различных ключа: К_в – открытый ключ отправителя А; k_в – секретный ключ получателя В. Генератор ключей целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ k_в по незащищенному каналу). Значения ключей К_в и k_в зависят от начального состояния генератора ключей.

Раскрытие секретного ключа k_в по известному открытому ключу К_в должно быть вычислительно неразрешимой задачей.

 

Рисунок 2.1- Обобщенная схема асимметричной криптосистемы с открытым ключом

 

Характерные особенности асимметричных криптосистем:

1. Открытый ключ К_в и криптограмма С могут быть отправлены по незащищенным каналам, т.е. противнику известны К_в и С.

2. Алгоритмы шифрования и расшифрования

Е_в : М ® С,

D_в : С ® М

являются открытыми.

Защита информации в асимметричной криптосистеме основана на секретности ключа k_в.

У.Диффи и М.Хеллман сформулировали требования, выполнение которых обеспечивает безопасность асимметричной криптосистемы:

1. Вычисление пары ключей (К_в, k_в) получателем В на основе начального условия должно быть простым.

2. Отправитель А, зная открытый ключ К_в и сообщение М, может легко вычислить криптограмму

С = 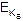(М) = Е_в (М) (2.1)

3. Получатель В, используя секретный ключ k_в и криптограмму С, может легко восстановить исходное сообщение

М = (С) = D_в(С) = D_в [Е_в(М)] (2.2)

4. Противник, зная открытый ключ К_в, при попытке вычислить секретный ключ k_в наталкивается на непреодолимую вычислительную проблему.

5. Противник, зная пару (К_в, С), при попытке вычислить исходное сообщение М наталкивается на непреодолимую вычислительную проблему.

 

Однонаправленные функции

Концепция асимметричных криптографических систем с открытым ключом основана на применении однонаправленных функций. Неформально однонаправленную функцию можно определить следующим образом. Пусть X и Y – некоторые произвольные множества. Функциf : X ® Y

является однонаправленной, если для всех xÎX можно легко вычислить функцию

y = f (x), где yÎY.

И в то же время для большинства yÎY достаточно сложно получить значение xÎX, такое, что f (x)=y (при этом полагают, что существует по крайней мере одно такое значение x).

Основным критерием отнесения функции f к классу однонаправленных функций является отсутствие эффективных алгоритмов обратного преобразования

Y ® X.

В качестве первого примера однонаправленной функции рассмотрим целочисленное умножение. Прямая задача – вычисление произведения двух очень больших целых чисел P и Q, т.е. нахождение значения

N = P*Q (2.3)

является относительно несложной задачей для ЭВМ.

Обратная задача – разложение на множители большого целого числа, т.е. нахождение делителей P и Q большого целого числа N = P*Q, является практически неразрешимой задачей при достаточно больших значениях N. По современным оценкам теории чисел при целом N»2⁶⁶⁴ и P»Q для разложения числа N потребуется около 10²³ операций, т.е. задача практически неразрешима на современных ЭВМ.

Следующий характерный пример однонаправленной функции – это модульная экспонента с фиксированными основанием и модулем. Пусть A и N – целые числа, такие, что 1£ А < N. Определим множество Z_N:

Z_N = {0, 1, 2, ..., N –1}.

Тогда модульная экспонента с основанием А по модулю N представляет собой функцию

f_A,N : Z_N ® Z_N,

f_A,N (x) = A^x (mod N) (2.4),

где X – целое число, 1£ x £ N –1.

Существуют эффективные алгоритмы, позволяющие достаточно быстро вычислить значения функции f_A,N (x).

Если y = A^x, то естественно записать x = log_A (у).

Поэтому задачу обращения функции f_A,N(x) называют задачей нахождения дискретного логарифма или задачей дискретного логарифмирования.

Задача дискретного логарифмирования формулируется следующим образом. Для известных целых A, N, y найти целое число x, такое, что

A^x mod N = y.

Алгоритм вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому модульная экспонента считается однонаправленной функцией.

По современным оценкам теории чисел при целых числах A » 2⁶⁶⁴ и N » 2⁶⁶⁴ решение задачи дискретного логарифмирования (нахождение показателя степени x для известного y) потребует около 10²⁶ операций, т.е. эта задача имеет в 10³ раз большую вычислительную сложность, чем задача разложения на множители. При увеличении длины чисел разница в оценках сложности задач возрастает.

Следует отметить, что пока не удалось доказать, что не существует эффективного алгоритма вычисления дискретного логарифма за приемлемое время. Исходя из этого, модульная экспонента отнесена к однонаправленным функциям условно, что, однако, не мешает с успехом применять ее на практике.

Вторым важным классом функций, используемых при построении криптосистем с открытым ключом, являются так называемые однонаправленные функции с "потайным ходом" (с лазейкой). Дадим неформальное определение такой функции. Функция

f : X ® Y

относится к классу однонаправленных функций с "потайным ходом" в том случае, если она является однонаправленной и, кроме того, возможно эффективное вычисление обратной функции, если известен "потайной ход" (секретное число, строка или другая информация, ассоциирующаяся с данной функцией).

В качестве примера однонаправленной функции с "потайным ходом" можно указать используемую в криптосистеме RSA модульную экспоненту с фиксированными модулем и показателем степени. Переменное основание модульной экспоненты используется для указания числового значения сообщения М либо криптограммы С.