Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Алгоритм RSA предложили в 1978 г. три автора: Р.Райвест (Rivest), А.Шамир (Shamir) и А.Адлеман (Adleman). Алгоритм получил свое название по первым буквам фамилий его авторов. Алгоритм RSA стал первым полноценным алгоритмом с открытым ключом, который может работать как в режиме шифрования данных, так и в режиме электронной цифровой подписи.

Надежность алгоритма основывается на трудности факторизации больших чисел и трудности вычисления дискретных логарифмов.

В криптосистеме RSA открытый ключ К_в, секретный ключ k_в, сообщение М и криптограмма С принадлежат множеству целых чисел

Z_N = {0, 1, 2, ..., N –1}, (2.5)

где N – модуль:

N = P*Q (2.6) .

Здесь P и Q – случайные большие простые числа. Для обеспечения максимальной безопасности выбирают P и Q равной длины и хранят в секрете.

Множество Z_N с операциями сложения и умножения по модулю N образует арифметику по модулю N.

Открытый ключ К_в выбирают случайным образом так, чтобы выполнялись условия:

1< К_в £ j (N), НОД (К_в, j (N)) =1, (2.7)

j (N)=(P –1) (Q –1), (2.8)

где j (N) – функция Эйлера.

Функция Эйлера j (N) указывает количество положительных целых чисел в интервале от 1 до N, которые взаимно проcты с N.

Второе из указанных выше условий означает, что открытый ключ К_в и функция Эйлера j (N) должны быть взаимно простыми.

Далее, используя расширенный алгоритм Евклида, вычисляют секретный ключ k_в, такой, что

k_в * К_в º 1 (mod j (N)) (2.9)

или

k_в = К_в^–1 (mod (P –1)(Q –1)).

Это можно осуществить, так как получатель В знает пару простых чисел (P,Q) и может легко найти j (N). Заметим, что k_в и N должны быть взаимно простыми.

Открытый ключ К_в используют для шифрования данных, а секретный ключ k_в – для расшифрования.

Преобразование шифрования определяет криптограмму С через пару (открытый ключ К_в, сообщение М) в соответствии со следующей формулой:

C = 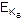(M) = E_В (M) = (mod N). (2.10)

В качестве алгоритма быстрого вычисления значения C используют ряд последовательных возведений в квадрат целого M и умножений на M с приведением по модулю N.

Обращение функции C = (mod N), т.е. определение значения M по известным значениям C, К_в и N, практически не осуществимо при N » 2 ⁵¹².

Однако обратную задачу, т.е. задачу расшифрования криптограммы С, можно решить, используя пару (секретный ключ k_в, криптограмма С) по следующей формуле:

М = (С) = D_В (C) = (mod N). (2.11)

Процесс расшифрования можно записать так:

D_В(E_В (М)) = М. (2.12)

Подставляя в (2.12) значения (2.10) и (2.11), получаем:

= М (mod N)

или

= M (mod N). (2.13)

Величина j (N) играет важную роль в теореме Эйлера, которая утверждает, что если НОД (x, N) =1, то

x^j(N) º 1 (mod N),

или в несколько более общей форме

x^n×j(N)+1 º x (mod N). (2.14)

Сопоставляя выражения (2.13) и (2.14), получаем

К_в * k_в = n * j (N) +1

или, что то же самое,

К_в * k_в º1 (mod j (N)).

Именно поэтому для вычисления секретного ключа k_в используют соотношение (2.9).

Таким образом, если криптограмму

C = (mod N)

возвести в степень k_в, то в результате восстанавливается исходный открытый текст М, так как

= = M^n×j(N)+1 º M (mod N).

Таким образом, получатель В, который создает криптосистему, защищает два параметра: 1) секретный ключ k_в и 2) пару чисел (P,Q), произведение которых дает значение модуля N. С другой стороны, получатель В открывает значение модуля N и открытый ключ К_в.

Противнику известны лишь значения К_в и N. Если бы он смог разложить число N на множители P и Q, то он узнал бы "потайной ход" – тройку чисел {P,Q,К_в}, вычислил значение функции Эйлера

j (N) = (P –1) (Q –1)

и определил значение секретного ключа k_в.

Однако, как уже отмечалось, разложение очень большого N на множители вычислительно не осуществимо (при условии, что длины выбранных P и Q составляют не менее 100 десятичных знаков).