Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Государственное образовательное учреждение высшего профессионального образования

«Поволжская государственная академия телекоммуникаций и информатики»

Кафедра ПДС

Методические разработки к лабораторным работам по дисциплине

«СРЕДСТВА ОБЕСПЕЧЕНИЯ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ В СЕТЯХ ПЕРЕДАЧИ ДАННЫХ»

для студентов специальностей 200900, 201000, 201800

 

 

Самара, 2005

 

 

Методические разработки к лабораторным работам по дисциплине «Средства обеспечения информационной безопасности в сетях передачи данных» / Сост. к.т.н., доц. А.В.Крыжановский,

д.т.н.,проф.А.А. Нерсесянц -Самара, 2005.-140 с. , ил.

 

Приведены методические указания к лабораторным работам, относящимся к основным разделам криптографии: симметричные и асимметричные криптосистемы, электронная цифровая подпись, управление криптографическими ключами и идентификация. Все методические указания снабжены краткими теоретическими сведениями.

Методические разработки утверждены на заседании кафедры ПДС 7.06.2005 г.,протокол № 8.

 

 

Редактор- д.т.н., проф. Б.Я.Лихтциндер

Рецензент-д.т.н. проф. В.Г. Карташевский

 

Лабораторная работа №1

ИЗУЧЕНИЕ ОТЕЧЕСТВЕННОГО СТАНДАРТА ШИФРОВАНИЯ ГОСТ 28147-89

Цель работы

Изучить основные принципы и особенности симметричного алгоритма шифрования по стандарту ГОСТ 28147-89.

 

Рекомендуемые источники

1. ГОСТ 28147-89. Система обработки информации. Защита крипотографическая. Алгоритм криптографического преобразования информации.

2. Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях /Под ред. В.Ф. Шаньгина – 2-е изд. перераб. и доп. – М.:Радио и связь,2001. с. 98-111.

3. Соколов А.В., Шаньгин В.Ф. Защита информации в распределенных корпоративных сетях и системах. – М.: ДМК Пресс, 2002, с. 181 – 194.

4. Б. Шнайер. Прикладная криптография. – М.: Триумф, 2002, с. 373 – 377.

5. Шеннон К.Э. Теория связи в секретных системах. В кн. К.Э. Шеннона «Работы по теории информации и кибернетике».- М.: ИЛ, 1963, - с. 243 – 332.

 

Подготовка к работе

1.Ознакомиться с алгоритмом шифрования ГОСТ 28147-89 по одному из рекомендованных источников /1 – 4/.

2.Ознакомиться с содержанием данной методической разработки.

3.Подготовить бланк отчета, который должен содержать:

- цель работы;

- блок-схему алгоритма в режиме простой замены;

- заготовки таблиц по п.8 задания;

- объяснение результатов шифрования и дешифрования.

 

4. Контрольные вопросы

1.Объясните сущность основных понятий: криптография, криптоанализ, конфиденциальность и целостность информации.

2.Обобщенная схема симметричной криптосистемы.

3.Обобщенная схема асимметричной криптосистемы.

4.Понятие криптостойкости системы шифрования.

5.Основные принципы криптоаналитических атак..

6.Сущность криптоаналитических атак при наличии открытого и зашифрованноготекстов.

7.Сущность криптоаналитических атак при возможности выбора открытого текста.

8.Сущность криптоаналитических атак с использованием выбранного шифротекста.

9.Сущность криптоаналитических атак методом полного перебора всехвозможных ключей (методом «грубой силы»).

10. Сущность принципа рассеивания.

11. Сущность принципа перемешивания.

12. Принцип шифрования по стандарту ГОСТ 28147-89.

13. Принцип расшифрования по стандарту ГОСТ 28147-89.

14. Процедуры подстановки и перестановки в стандарте ГОСТ 28147-89.

15. Достоинства и недостатки шифрования по стандарту ГОСТ 28147-89.

 

Содержание работы

1.

Ознакомиться с алгоритмом и реализационными основами шифрования по ГОСТ 28147-89.

2.Изучить основные этапы шифрования на компьютерной модели.

3.Изучить основные особенности алгоритма по стандарту ГОСТ 28147-89.

 

Содержание отчета

1.Цель работы.

2.Структурную схему алгоритма шифрования по стандарту ГОСТ 28147-89 в режиме простой замены.

3.Таблицы шифрования и дешифрования.

4.Выводы о технических возможностях, особенностях, преимуществах и областях применения алгоритма по стандарту ГОСТ 28147-89.

 

Общие сведения

Принципы криптографической защиты

Информации

Криптография представляет собой совокупность методов преобразования данных, направленных на то, чтобы сделать эти данные бесполезными для противника. Такие преобразования позволяют решить две главные проблемы защиты данных: проблему конфиденциальности (путем лишения противника возможности извлечь информацию из канала связи) и проблему целостности (путем лишения противника возможности изменить сообщение так, чтобы изменился его смысл, или ввести ложную информацию в канал связи).

Проблемы конфиденциальности и целостности информации тесно связаны между собой, поэтому методы решения одной из них часто применимы для решения другой.

Обобщенная схема криптографической системы, обеспечивающей шифрование передаваемой информации, показана на рис.1.1. Отправитель генерирует открытый текст исходного сообщения М, которое должно быть передано законному получателю по незащищенному каналу. За каналом следит перехватчик с целью перехватить и раскрыть передаваемое сообщение. Для того чтобы перехватчик не смог узнать содержание сообщения М, отправитель шифрует его с помощью обратимого преобразования Е_К и получает шифртекст (или криптограмму) С = Е_К (М), который отправляет получателю.

Рисунок1.1- Обобщенная схема криптосистемы

 

Законный получатель, приняв шифртекст С, расшифровывает его с помощью обратного преобразования D = Е_К^–1 и получает исходное сообщение в виде открытого текста М:

D_K (C) = Е_К^–1 (Е_К (М)) = M.

Преобразование Е_К выбирается из семейства криптографических преобразований, называемых криптоалгоритмами,. Параметр, с помощью которого выбирается отдельное используемое преобразование, называется криптографическим ключом К. Криптосистема имеет разные варианты реализации: набор инструкций, аппаратные средства, комплекс программ компьютера, которые позволяют зашифровать открытый текст и расшифровать шифр-текст различными способами, один из которых выбирается с помощью конкретного ключа К.

Говоря более формально, криптографическая система – это однопараметрическое семейство обратимых преобразований

Е_К : ®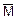

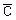
из пространства 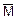сообщений открытого текста в пространство 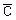шифрованных текстов. Параметр К (ключ) выбирается из конечного множества , называемого пространством ключей.

Вообще говоря, преобразование шифрования может быть симметричным или асимметричным относительно преобразования расшифрования. Это важное свойство функции преобразования определяет два класса криптосистем:

· симметричные (одноключевые) криптосистемы;

· асимметричные (двухключевые) криптосистемы (с открытым ключом).

Схема симметричной криптосистемы с одним секретным ключом была показана на рис.1.1. В ней используются одинаковые секретные ключи в блоке шифрования и блоке расшифрования.

Обобщенная схема асимметричной криптосистемы с двумя разными ключами К₁ и К₂ показана на рис.1.2. В этой криптосистеме один из ключей является открытым, а другой – секретным.

В симметричной криптосистеме секретный ключ надо передавать отправителю и получателю по защищенному каналу распространения ключей, например такому, как курьерская служба. На рис.1.1 этот канал показан "экранированной" линией. Существуют и другие способы распределения секретных ключей, они будут рассмотрены позднее. В асимметричной криптосистеме передают по незащищенному каналу только открытый ключ, а секретный ключ сохраняют на месте его генерации.

 

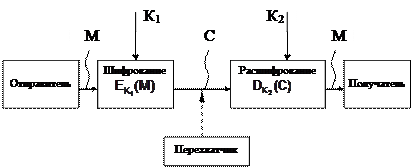
Рисунок 1.2- Обобщенная схема асимметричной криптосистемы с открытым ключом

 

На рис.1.3 показан поток информации в криптосистеме в случае активных действий перехватчика. Активный перехватчик не только считывает все шифртексты, передаваемые по каналу, но может также пытаться изменять их по своему усмотрению.

Любая попытка со стороны перехватчика расшифровать шифртекст С для получения открытого текста М или зашифровать свой собственный текст М’ для получения правдоподобного шифртекста С’, не имея подлинного ключа, называется крипто-аналитической атакой.

Если предпринятые криптоаналитические атаки не достигают поставленной цели и криптоаналитик не может, не имея подлинного ключа, вывести М из С или С’ из М’, то полагают, что такая криптосистема является криптостойкой.

 

 

Рисунок1. 3- Поток информации в криптосистеме при активном перехвате сообщений

 

Криптоанализ – это наука о раскрытии исходного текста зашифрованного сообщения без доступа к ключу. Успешный анализ может раскрыть исходный текст или ключ. Он позволяет также обнаружить слабые места в криптосистеме, что, в конечном счете, ведет к тем же результатам.

Фундаментальное правило криптоанализа, впервые сформулированное голландцем А.Керкхоффом еще в XIX веке заключается в том, что стойкость шифра (криптосистемы) должна определяться только секретностью ключа. Иными словами, правило Керкхоффа состоит в том, что весь алгоритм шифрования, кроме значения секретного ключа, известен криптоаналитику противника. Это обусловлено тем, что криптосистема, реализующая семейство криптографических преобразований, обычно рассматривается как открытая система. Такой подход отражает очень важный принцип технологии защиты информации: защищенность системы не должна зависеть от секретности чего-либо такого, что невозможно быстро изменить в случае утечки секретной информации. Обычно криптосистема представляет собой совокупность аппаратных и программных средств, которую можно изменить только при значительных затратах времени и средств, тогда как ключ является легко изменяемым объектом. Именно поэтому стойкость криптосистемы определяется только секретностью ключа.

Другое почти общепринятое допущение в криптоанализе состоит в том, что криптоаналитик имеет в своем распоряжении шифртексты сообщений.

Существует четыре основных типа криптоаналитических атак. Конечно, все они формулируются в предположении, что криптоаналитику известны применяемый алгоритм шифрования и шифртексты сообщений. Перечислим эти криптоаналитические атаки.

 

Основные виды шифрования

Большинство средств защиты информации базируется на использовании криптографических шифров и процедур шифрования-расшифрования. В соответствии со стандартом ГОСТ 28147-89 под шифром понимают совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, задаваемых ключом и алгоритмом криптографического преобразования.

Ключ – это конкретное секретное состояние некоторых параметров алгоритма криптографического преобразования данных, обеспечивающее выбор только одного варианта из всех возможных для данного алгоритма /1/.

Основной характеристикой шифра является криптостойкость, которая определяет его стойкость к раскрытию методами криптоанализа. Обычно эта характеристика определяется интервалом времени, необходимым для раскрытия шифра.

К шифрам, используемым для криптографической защиты информации, предъявляется ряд требований:

· достаточная криптостойкость (надежность закрытия данных);

· простота процедур шифрования и расшифрования;

· незначительная избыточность информации за счет шифрования;

· нечувствительность к небольшим ошибкам шифрования и др.

В той или иной мере этим требованиям отвечают:

· шифры перестановок;

· шифры замены;

· шифры гаммирования;

· шифры, основанные на аналитических преобразованиях шифруемых данных.

Шифрование перестановкой заключается в том, что символы шифруемого текста переставляются по определенному правилу в пределах некоторого блока этого текста. При достаточной длине блока, в пределах которого осуществляется перестановка, и сложном неповторяющемся порядке перестановки можно достигнуть приемлемой для простых практических приложений стойкости шифра.

Шифрование заменой (подстановкой) заключается в том, что символы шифруемого текста заменяются символами того же или другого алфавита в соответствии с заранее обусловленной схемой замены.

Шифрование гаммированием заключается в том, что символы шифруемого текста складываются с символами некоторой случайной последовательности, именуемой гаммой шифра. Стойкость шифрования определяется в основном длиной (периодом) неповторяющейся части гаммы шифра. Поскольку с помощью ЭВМ можно генерировать практически бесконечную гамму шифра, то данный способ является одним из основных для шифрования информации в автоматизированных системах.

Шифрование аналитическим преобразованием заключается в том, что шифруемый текст преобразуется по некоторому аналитическому правилу (формуле).

Например, можно использовать правило умножения вектора на матрицу, причем умножаемая матрица является ключом шифрования (поэтому ее размер и содержание должны храниться в секрете), а символами умножаемого вектора последовательно служат символы шифруемого текста. Другим примером может служить использование так называемых однонаправленных функций для построения криптосистем с открытым ключом.

 

По мнению К. Шеннона /5/, в практических шифрах необходимо использовать два основных общих принципа: рассеивание и перемешивание.

Рассеивание представляет собой распространение влияния одного знака открытого текста на много знаков шифртекста, что позволяет скрыть статистические свойства открытого текста.

Перемешивание предполагает использование таких шифрующих преобразований, которые усложняют восстановление взаимосвязи статистических свойств открытого и шифрованного текстов. Однако шифр должен не только затруднять раскрытие, но и обеспечивать легкость зашифрования и расшифрования при известном пользователю секретном ключе.

Распространенным способом достижения эффектов рассеивания и перемешивания является использование составного шифра, т.е. такого шифра, который может быть реализован в виде некоторой последовательности простых шифров, каждый из которых вносит свой вклад в значительное суммарное рассеивание и перемешивание.

В составных шифрах в качестве простых шифров чаще всего используются простые перестановки и подстановки. При перестановке просто перемешивают символы открытого текста, причем конкретный вид перемешивания определяется секретным ключом. При подстановке каждый символ открытого текста заменяют другим символом из того же алфавита, а конкретный вид подстановки также определяется секретным ключом. Следует заметить, что в современном блочном шифре блоки открытого текста и шифртекста представляют собой двоичные последовательности обычно длиной 64 бита. В принципе каждый блок может принимать 2⁶⁴ значений. Поэтому подстановки выполняются в очень большом алфавите, содержащем до 2⁶⁴ » 10¹⁹ "символов".

При многократном чередовании простых перестановок и подстановок, управляемых достаточно длинным секретным ключом, можно получить очень стойкий шифр с хорошим рассеиванием и перемешиванием. Рассмотренные ниже криптоалгоритмы DES, IDEA и отечественный стандарт шифрования данных построен в полном соответствии с указанной методологией.

 

Режим простой замены

Для реализации алгоритма шифрования данных в режиме простой замены используется только часть блоков общей криптосистемы (рис.1.4). Обозначения на схеме:

N₁, N₂ – 32-разрядные накопители;

СМ₁ – 32-разрядный сумматор по модулю 2³² (⊞);

СМ₂ – 32-разрядный сумматор по модулю 2 (Å);

R – 32-разрядный регистр циклического сдвига;

КЗУ – ключевое запоминающее устройство на 256 бит, состоящее из восьми 32-разрядных накопителей Х₀, Х₁, Х₂, ..., Х₇;

S – блок подстановки, состоящий из восьми узлов замены (S-блоков замены) S₁, S₂, S₃, ..., S₇, S₈.

 

Цель работы

Изучить принципы и процедурные аспекты криптосистемы RSA.

 

Рекомендуемые источники

1.Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях /Под ред. В.Ф. Шаньгина.- 2-е изд.. перераб. и доп..-М.: Радио и связь, 2001, с. 131-138.

2.Соколов А.В., Шаньгин В.Ф. Защита информации в распределенных корпоративных сетях и системах.- М.: ДМК Пресс, 2002, с. 204-206.

3.Б. Шнайер. Прикладная криптография.-М.: Триумф, 2002, с. 521-530.

 

Подготовка к работе

1.Ознакомиться с алгоритмом шифрования по одному из рекомендованных источников/1-3/.

2.Ознакомиться с содержанием данной методической

разработки.

3.Подготовить бланк отчета, который должен содержать:

- цель работы;

- основные математические соотношения формирования ключевой информации.

 

4. Контрольные вопросы

1.

Изобразите обобщенную схему асимметричной криптосистемы.

2.Характерные особенности асимметричных криптосистем.

3.Основные требования, обеспечивающие безопасность асимметричной криптосистемы.

4.Понятие однонаправленных функций.

5.Сущность алгоритма шифрования RSA.

6.Сущность процедуры шифрования в системе RSA.

7.Сущность процедуры расшифрования в системе RSA.

8.Требования, предъявляемые к исходным параметрам системы RSA для формирования ключевой информации.

 

Содержание работы

1.Ознакомиться с алгоритмом RSA и его основными особенностями.

2.Изучить основные этапы шифрования на компьютерной модели.

3.Произвести установку открытых и закрытых ключей для двух абонентов.

4.Произвести двухсторонний обмен информацией.

 

Содержание отчета

Отчет должен содержать:

1.Цель работы.

2.Структурную схему асимметричной криптосистемы с открытым ключом.

3.Основные математические соотношения формирования ключевой информации.

4.Таблицы шифрования и дешифрования.

5.Выводы о технических возможностях, особенностях, преимуществах и областях применения алгоритма RSA.

 

Общие сведения

Однонаправленные функции

Концепция асимметричных криптографических систем с открытым ключом основана на применении однонаправленных функций. Неформально однонаправленную функцию можно определить следующим образом. Пусть X и Y – некоторые произвольные множества. Функциf : X ® Y

является однонаправленной, если для всех xÎX можно легко вычислить функцию

y = f (x), где yÎY.

И в то же время для большинства yÎY достаточно сложно получить значение xÎX, такое, что f (x)=y (при этом полагают, что существует по крайней мере одно такое значение x).

Основным критерием отнесения функции f к классу однонаправленных функций является отсутствие эффективных алгоритмов обратного преобразования

Y ® X.

В качестве первого примера однонаправленной функции рассмотрим целочисленное умножение. Прямая задача – вычисление произведения двух очень больших целых чисел P и Q, т.е. нахождение значения

N = P*Q (2.3)

является относительно несложной задачей для ЭВМ.

Обратная задача – разложение на множители большого целого числа, т.е. нахождение делителей P и Q большого целого числа N = P*Q, является практически неразрешимой задачей при достаточно больших значениях N. По современным оценкам теории чисел при целом N»2⁶⁶⁴ и P»Q для разложения числа N потребуется около 10²³ операций, т.е. задача практически неразрешима на современных ЭВМ.

Следующий характерный пример однонаправленной функции – это модульная экспонента с фиксированными основанием и модулем. Пусть A и N – целые числа, такие, что 1£ А < N. Определим множество Z_N:

Z_N = {0, 1, 2, ..., N –1}.

Тогда модульная экспонента с основанием А по модулю N представляет собой функцию

f_A,N : Z_N ® Z_N,

f_A,N (x) = A^x (mod N) (2.4),

где X – целое число, 1£ x £ N –1.

Существуют эффективные алгоритмы, позволяющие достаточно быстро вычислить значения функции f_A,N (x).

Если y = A^x, то естественно записать x = log_A (у).

Поэтому задачу обращения функции f_A,N(x) называют задачей нахождения дискретного логарифма или задачей дискретного логарифмирования.

Задача дискретного логарифмирования формулируется следующим образом. Для известных целых A, N, y найти целое число x, такое, что

A^x mod N = y.

Алгоритм вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому модульная экспонента считается однонаправленной функцией.

По современным оценкам теории чисел при целых числах A » 2⁶⁶⁴ и N » 2⁶⁶⁴ решение задачи дискретного логарифмирования (нахождение показателя степени x для известного y) потребует около 10²⁶ операций, т.е. эта задача имеет в 10³ раз большую вычислительную сложность, чем задача разложения на множители. При увеличении длины чисел разница в оценках сложности задач возрастает.

Следует отметить, что пока не удалось доказать, что не существует эффективного алгоритма вычисления дискретного логарифма за приемлемое время. Исходя из этого, модульная экспонента отнесена к однонаправленным функциям условно, что, однако, не мешает с успехом применять ее на практике.

Вторым важным классом функций, используемых при построении криптосистем с открытым ключом, являются так называемые однонаправленные функции с "потайным ходом" (с лазейкой). Дадим неформальное определение такой функции. Функция

f : X ® Y

относится к классу однонаправленных функций с "потайным ходом" в том случае, если она является однонаправленной и, кроме того, возможно эффективное вычисление обратной функции, если известен "потайной ход" (секретное число, строка или другая информация, ассоциирующаяся с данной функцией).

В качестве примера однонаправленной функции с "потайным ходом" можно указать используемую в криптосистеме RSA модульную экспоненту с фиксированными модулем и показателем степени. Переменное основание модульной экспоненты используется для указания числового значения сообщения М либо криптограммы С.

Цель работы

Изучить особенности посимвольного шифрования на основе криптосистемы RSA.

 

Рекомендуемые источники

1.Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях /Под ред. В.Ф. Шаньгина.- 2-е изд.. перераб. и доп..-М.: Радио и связь, 2001, с. 131-138.

2.Соколов А.В., Шаньгин В.Ф. Защита информации в распределенных корпоративных сетях и системах.- М.: ДМК Пресс, 2002, с. 204-206.

3.Б. Шнайер. Прикладная криптография.-М.: Триумф, 2002, с. 521-530.

4.Методические указания к проведению лабораторной работы «Обмен зашифрованными сообщениями с помощью программы PGP» сост. Алексеев А.П., ПГАТИ. 2002.

 

Подготовка к работе

1.Ознакомиться с алгоритмом шифрования по одному из рекомендованных источников /1-3/.

2.Ознакомиться с содержанием данной методической разработки.

3.Подготовить бланк отчета, который должен содержать:

- цель работы;

- основные математические соотношения формирования ключевой информации.

 

4. Контрольные вопросы

1.Сущность посимвольного шифрования на основе криптосистемы RSA.

2.Особенности посимвольного шифрования на основе RSA с использованием кода ASCII.

3.Достоинства посимвольного шифрования.

4.Недостатки посимвольного шифрования.

5.Сущность поточного шифрования.

6.Особенности блочного шифрования.

7.Сущность систем шифрования с обратной связью.

8.Достоинства блочного шифрования.

 

Содержание работы

1.Ознакомиться с основными особенностями посимвольного шифрования.

2.Изучить особенности кодирования буквенно-цифровых текстов на основе международного стандарта ASCII.

3.Произвести установку ключей в криптосистеме RSA.

4.Произвести шифрование и расшифрование произвольного текста посимвольным методом в криптосистеме RSA.

 

Содержание отчета

1.Цель работы.

2.Основные математические соотношения формирования ключевой информации в криптосистеме RSA.

3.По результатам выполнения п.5.4 представьте строки открытого и шифрованного текстов, располагая соответствующие буквы обоих текстов одну под другой.

4.Выводы о свойствах и эффективности асимметричного посимвольного шифрования.

 

 

Общие сведения

Блочные и поточные шифры

Проектирование алгоритмов шифрования данных основано на рациональном выборе функций, преобразующих исходные (незашифрованные) сообщения в шифртекст. Идея непосредственного применения такой функции ко всему сообщению реализуется очень редко. Практически все применяемые криптографические методы связаны с разбиением сообщения на большое число фрагментов (или знаков) фиксированного размера, каждый из которых шифруется отдельно. Такой подход существенно упрощает задачу шифрования, так как сообщения обычно имеют различную длину.

Различают три основных способа шифрования: поточные шифры, блочные шифры и блочные шифры с обратной связью. Для классификации методов шифрования данных следует выбрать некоторое количество характерных признаков, которые можно применить для установления различий между этими методами. Будем полагать, что каждая часть или каждый знак сообщения шифруется отдельно в заданном порядке.

 

Можно выделить следующие характерные признаки методов шифрования данных.

·

Выполнение операций с отдельными битами или блоками. Известно, что для некоторых методов шифрования знаком сообщения, над которым производят операции шифрования, является отдельный бит, тогда как другие методы оперируют конечным множеством битов, обычно называемым блоком.

· Зависимость или независимость функции шифрования от результатов шифрования предыдущих частей сообщения.

· Зависимость или независимость шифрования отдельных знаков от их положения в тексте. В некоторых методах знаки шифруются с использованием одной и той же функции независимо от их положения в сообщении, а в других методах, например при поточном шифровании, различные знаки сообщения шифруются с учетом их положения в сообщении. Это свойство называют позиционной зависимостью или независимостью шифра.

· Симметрия или асимметрия функции шифрования. Эта важная характеристика определяет существенное различие между обычными симметричными (одноключевыми) криптосистемами и асимметричными (двухключевыми) криптосистемами с открытым ключом. Основное различие между ними состоит в том, что в асимметричной криптосистеме знания ключа шифрования (или расшифрования) недостаточно для раскрытия соответствующего ключа расшифрования (или шифрования).

 

В табл.3.3 приведены типы криптосистем и их основные характеристики.

 

Таблица 3.3- Основные характеристики криптосистем

Тип крипто- системы	Операции с битами или блоками	Зависимость от предыдущих знаков	Пози-ционная зависи-мость	Наличие симметрии функции шифрования
Поточного шифрования	Биты	Не зависит	Зависит	Симметричная
Блочного шифрования	Блоки	Не зависит	Не зависит	Симметричная или несимметрич-ная
С обратной связью по шифртексту	Биты или блоки	Зависит	Не зависит	Симметричная

 

Поточное шифрование состоит в том, что биты открытого текста складываются по модулю 2 с битами псевдослучайной последовательности. К достоинствам поточных шифров относятся высокая скорость шифрования, относительная простота реализации и отсутствие размножения ошибок. Недостатком является необходимость передачи информации синхронизации перед заголовком сообщения, которая должна быть принята до расшифрования любого сообщения. Это обусловлено тем, что если два различных сообщения шифруются на одном и том же ключе, то для расшифрования этих сообщений требуется одна и та же псевдослучайная последовательность. Такое положение может создать угрозу криптостойкости системы. Поэтому часто используют дополнительный, случайно выбираемый ключ сообщения, который передается в начале сообщения и применяется для модификации ключа шифрования. В результате разные сообщения будут шифроваться с помощью различных последовательностей.

Поточные шифры широко применяются для шифрования преобразованных в цифровую форму речевых сигналов и цифровых данных, требующих оперативной доставки потребителю информации. До недавнего времени такие применения были преобладающими для данного метода шифрования. Это обусловлено, в частности, относительной простотой проектирования и реализации генераторов хороших шифрующих последовательностей. Но самым важным фактором, конечно, является отсутствие размножения ошибок в поточном шифре. Стандартным методом генерирования последовательностей для поточного шифрования является метод, применяемый в стандарте шифрования DES в режиме обратной связи по выходу (режим OFB).

При блочном шифровании открытый текст сначала разбивается на равные по длине блоки, затем применяется зависящая от ключа функция шифрования для преобразования блока открытого текста длиной m бит в блок шифртекста такой же длины. Достоинством блочного шифрования является то, что каждый бит блока шифртекста зависит от значений всех битов соответствующего блока открытого текста, и никакие два блока открытого текста не могут быть представлены одним и тем же блоком шифртекста. Алгоритм блочного шифрования может использоваться в различных режимах. Четыре режима шифрования алгоритма DES фактически применимы к любому блочному шифру: режим прямого шифрования или шифрования с использованием электронной книги кодов ЕСВ (Electronic code Book), шифрование со сцеплением блоков шифртекста СВС (Cipher block chaining), шифрование с обратной связью по шифртексту CFB (Cipher feedback) и шифрование с обратной связью по выходу OFB (Output feedback).

Основным достоинством прямого блочного шифрования ECB является то, что в хорошо спроектированной системе блочного шифрования небольшие изменения в шифртексте вызывают большие и непредсказуемые изменения в соответствующем открытом тексте, и наоборот. Вместе с тем применение блочного шифра в данном режиме имеет серьезные недостатки. Первый из них заключается в том, что вследствие детерминированного характера шифрования при фиксированной длине блока 64 бита можно осуществить криптоанализ шифртекста "со словарем" в ограниченной форме. Это обусловлено тем, что идентичные блоки открытого текста длиной 64 бита в исходном сообщении представляются идентичными блоками шифртекста, что позволяет криптоаналитику сделать определенные выводы о содержании сообщения. Другой потенциальный недостаток этого шифра связан с размножением ошибок. Результатом изменения только одного бита в принятом блоке шифртекста будет неправильное расшифрование всего блока. Это, в свою очередь, приведет к появлению искаженных битов (от 1 до 64) в восстановленном блоке исходного текста.

Из-за отмеченных недостатков блочные шифры редко применяются в указанном режиме для шифрования длинных сообщений. Однако в финансовых учреждениях, где сообщения часто состоят из одного или двух блоков, блочные шифры широко используют в режиме прямого шифрования. Такое применение обычно связано с возможностью частой смены ключа шифрования, поэтому вероятность шифрования двух идентичных блоков открытого текста на одном и том же ключе очень мала.

Криптосистема с открытым ключом также является системой блочного шифрования и должна оперировать блоками довольно большой длины. Это обусловлено тем, что криптоаналитик знает открытый ключ шифрования и мог бы заранее вычислить и составить таблицу соответствия блоков открытого текста и шифртекста. Если длина блоков мала, например 30 бит, то число возможных блоков не слишком большое (при длине 30 бит это 2³⁰ = ~10⁹), и может быть составлена полная таблица, позволяющая моментально расшифровать любое сообщение с использованием известного открытого ключа. Асимметричные криптосистемы с открытым ключом подробно разбираются в следующей главе.

Наиболее часто блочные шифры применяются в системах шифрования с обратной связью. Системы шифрования с обратной связью встречаются в различных практических вариантах. Как и при блочном шифровании, сообщения разбивают на ряд блоков, состоящих из m бит. Для преобразования этих блоков в блоки шифртекста, которые также состоят из m бит, используются специальные функции шифрования. Однако если в блочном шифре такая функция зависит только от ключа, то в блочных шифрах с обратной связью она зависит как от ключа, так и от одного или более предшествующих блоков шифртекста.

Практически важным шифром с обратной связью является шифр со сцеплением блоков шифртекста СВС. В этом случае m бит предыдущего шифртекста суммируются по модулю 2 со следующими m битами открытого текста, а затем применяется алгоритм блочного шифрования под управлением ключа для получения следующего блока шифртекста. Еще один вариант шифра с обратной связью получается из стандартного режима CFB алгоритма DES, т.е. режима с обратной связью по шифртексту.

Достоинством криптосистем блочного шифрования с обратной связью является возможность применения их для обнаружения манипуляций сообщениями, произв