Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Предположим, что пользователь А хочет передать пользователю В сообщение в зашифрованном виде, используя криптосистему RSA. В таком случае пользователь А выступает в роли отправителя сообщения, а пользователь В – в роли получателя. Как отмечалось выше, криптосистему RSA должен сформировать получатель сообщения, т.е. пользователь В. Рассмотрим последовательность действий пользователя В и пользователя А.

1. Пользователь В выбирает два произвольных больших простых числа P≠Q.

2. Пользователь В вычисляет значение модуля N = P * Q.

3. Пользователь В вычисляет функцию Эйлера

j (N) = (P –1) (Q –1)

и выбирает случайным образом значение открытого ключа К_в с учетом выполнения условий:

1< К_в £ j (N), НОД (К_в, j (N)) =1.

4. Пользователь В вычисляет значение секретного ключа k_в, используя расширенный алгоритм Евклида при решении сравнения

k_в º К_в^–1 (mod j (N)).

5. Пользователь В пересылает пользователю А пару чисел (N, К_в) по незащищенному каналу.

Если пользователь А хочет передать пользователю В сообщение М, он выполняет следующие шаги.

6. Пользователь А разбивает исходный открытый текст М на блоки, каждый из которых может быть представлен в виде числа

М_i = 0, 1, 2, ..., N –1.

7. Пользователь А шифрует текст, представленный в виде последовательности чисел М_i по формуле

C_i = 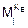(mod N)

и отправляет криптограмму

С₁, С₂, С₃, ..., C_i, ...

пользователю В.

8. Пользователь В расшифровывает принятую криптограмму

С₁, С₂, С₃, ..., C_i, ...,

используя секретный ключ k_в, по формуле

М_i = (mod N).

В результате будет получена последовательность чисел М_i, которые представляют собой исходное сообщение М. Чтобы алгоритм RSA имел практическую ценность, необходимо иметь возможность без существенных затрат генерировать большие простые числа, уметь оперативно вычислять значения ключей К_в и k_в.

 

Лабораторная работа №3

 

ИЗУЧЕНИЕ ПОСИМВОЛЬНОГО ШИФРОВАНИЯ НА ОСНОВЕ КРИПТОСИСТЕМЫ RSA

 

Цель работы

Изучить особенности посимвольного шифрования на основе криптосистемы RSA.

 

Рекомендуемые источники

1.Романец Ю.В., Тимофеев П.А., Шаньгин В.Ф. Защита информации в компьютерных системах и сетях /Под ред. В.Ф. Шаньгина.- 2-е изд.. перераб. и доп..-М.: Радио и связь, 2001, с. 131-138.

2.Соколов А.В., Шаньгин В.Ф. Защита информации в распределенных корпоративных сетях и системах.- М.: ДМК Пресс, 2002, с. 204-206.

3.Б. Шнайер. Прикладная криптография.-М.: Триумф, 2002, с. 521-530.

4.Методические указания к проведению лабораторной работы «Обмен зашифрованными сообщениями с помощью программы PGP» сост. Алексеев А.П., ПГАТИ. 2002.

 

Подготовка к работе

1.Ознакомиться с алгоритмом шифрования по одному из рекомендованных источников /1-3/.

2.Ознакомиться с содержанием данной методической разработки.

3.Подготовить бланк отчета, который должен содержать:

- цель работы;

- основные математические соотношения формирования ключевой информации.

 

4. Контрольные вопросы

1.Сущность посимвольного шифрования на основе криптосистемы RSA.

2.Особенности посимвольного шифрования на основе RSA с использованием кода ASCII.

3.Достоинства посимвольного шифрования.

4.Недостатки посимвольного шифрования.

5.Сущность поточного шифрования.

6.Особенности блочного шифрования.

7.Сущность систем шифрования с обратной связью.

8.Достоинства блочного шифрования.

 

Содержание работы

1.Ознакомиться с основными особенностями посимвольного шифрования.

2.Изучить особенности кодирования буквенно-цифровых текстов на основе международного стандарта ASCII.

3.Произвести установку ключей в криптосистеме RSA.

4.Произвести шифрование и расшифрование произвольного текста посимвольным методом в криптосистеме RSA.

 

Содержание отчета

1.Цель работы.

2.Основные математические соотношения формирования ключевой информации в криптосистеме RSA.

3.По результатам выполнения п.5.4 представьте строки открытого и шифрованного текстов, располагая соответствующие буквы обоих текстов одну под другой.

4.Выводы о свойствах и эффективности асимметричного посимвольного шифрования.