Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

(метод К.Е.Егорова)

 

Схема расчета осадки методом линейно-деформируемого слоя используется в случаях, если:

1. В пределах сжимаемой толщи грунта основания Н_С, определенной методом суммирования как для линейно-деформируемого полупространства, залегает слой грунта с модулем деформации Е₁≥100 МПа (1000 кг/см²) и толщина этого слоя h₁ удовлетворяет условию 6. п. 2.40, СНиП 2.02.01-83* [6]

, (2.10.1)

где-Е₁ и Е₂ – соответственно модуль деформации первого (выше расположенного) и второго (подстилающего) слоев грунта;

2. Ширина или диаметр фундамента b≥10 м и модуль деформации грунтов основания Е≥10 МПа (100 кг/см²);

3. Ширина фундамента b≥10 м при наличии в пределах сжимаемой толщи слоев грунта с модулем деформации Е≥10 МПа (100 кг/см²), при условии, если их суммарная толщина не превышает 0,2Н_С.

В случае 1 и 2 толщина сжимаемого слоя Н_С принимается до фактической кровли малосжимаемого грунта.

Для случая 3 толща линейно-деформируемого слоя грунта вычисляется по формуле 8. п.п. 8, обязательного приложения 2 [6]:

 

Н=(Н₀+ψ·b)·k_p, (2.10.2)

 

где Н₀ принимается для оснований сложенных пылевато-глинистыми грунтами 9м, песчаными – 6 м; ψ – соответственно для пылевато-глинистых грунтов 0,15, песчаных – 0,1, или по таблице 2.10.1;

Таблица 2.10.1

№№ п.п.	Наименование грунтов	Н0, м.	ψ
	Песок		0,10
	Пылевато-глинистые грунты		0,15

b -ширина подошвы фундамента, м; k_p – коэффициент, принимаемый: k_p=0,8, при среднем давлении под подошвой фундамента Р=100 кПа (1 кг/см²); k_p=1,2 при Р=500 кПа (5 кг/см²), при промежуточных значениях средних давлений Р величина k_p принимается по линейной интерполяции.

Если основание сложено пылевато-глинистыми и песчаными грунтами, значение толщи линейно-деформируемого слоя грунта Н определяется по формуле 9 п. 8 обязательного приложения 2 [6]:

Н=Н_S+ , (2.10.3)

где Н_S –толща слоя, вычисленная по формуле (2.10.2) в предположении, что основание сложено только песчаными грунтами;

h_cl –суммарная толщина слоев пылевато-глинистых грунтов в пределах от подошвы фундамента до глубины, равной Н_cl – значению Н, вычисленному по формуле (2.10.2) в предположении, что основание сложено только песчаными грунтами.

Значение Н, вычисленное по формулам (2.10.2) и (2.10.3), должно быть увеличено на толщину слоя грунта с модулем деформации Е<10 МПа (100 кг/см²), если этот слой расположен ниже Н, и толщина его не превышает 0,2 Н. При большей толщине слоя такого грунта, а так же, если вышележащие слои имеют модуль деформации Е<10 МПа (100 кг/см²), расчет деформаций основания выполняется по расчетной схеме линейно-деформируемого полупространства [6]. Схемы к расчету осадки фундамента методом линейно-деформируемого слоя представлены на рисунке 2.10.1.

а) б)

 

Рис. 2.10.1. Схема к расчету осадки фундамента методом линейно-деформируемого слоя:

а - схема плитного фундамента, совмещенного с геологическим разрезом;
б - схема к расчету осадки фундамента; 3-подошва i-го слоя грунта; 4 - нижняя граница сжимаемой толщи

 

Осадка основания с использованием расчетной схемы линейно-деформируемого слоя, в соответствии с требованиями п. 2.40 и п.7 обязательного приложения 2 [6] определяется по формуле

 

, (2.10.4)

 

где р	– среднее давление под подошвой фундамента (для фундаментов шириной b<10м принимается p=po–σzg,o), кПа;
b	– ширина прямоугольного или диаметр круглого фундамента, м;
kc и km	– коэффициенты, принимаемые по таблицам 2.10.2 и 2.10.3.

 

Коэффициент k_c

Таблица 2.10.2

Относительная толщина слоя ξI=	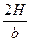Коэффициент kc
0<ξI≤0,5 0,5<ξI≤1 1<ξI≤2 2<ξI≤3 3<ξI≤5 ξI>5	1,5 1,4 1,3 1,2 1,1 1,0

 

Коэффициент k_m

Таблица 2.10.3

Среднее значение модуля деформации грунта основания Е, МПа (кг/см2)	Значение коэффициента km при ширине фундамента b, м
b<10	10≤b≤15	b>15
Е<10 (100)
Е≥10 (100)		1,35	1,5

 

n	–число слоев, различающихся по сжимаемости в пределах расчетной толщины слоя Н, определяемой по формуле Н=(Н0+ψ·b)·kp, (2);
ki и ki-1	-коэффициенты, определяемые по таблице 2.10.4 в зависимости от формы фундамента, соотношения сторон прямоугольного фундамента и относительной глубины, на которой расположены подошва и кровля i-го слоя соответственно ξi= и ξi-1= ;
Еi	-модуль деформации i-го соля грунта.

Формула (2.10.4) служит для определения средней осадки основания, загруженного равномерно-распределенной по ограниченной площади нагрузкой. Эту формулу допускается применять для определения осадки жестких фундаментов.

 

Коэффициент k

Таблица 2.10.4

ξ=	Коэффициент k для фундаментов
круглых	прямоугольных с отношением сторон η=l/b, равным	ленточных η=l/b≥10
	1,4	1,8	2,4	3,2
1	2	3	4	5	6	7	8	9
0,0 0,4 0,8 1,2 1,6 2.0	0,000 0,090 0,179 0,266 0,348 0,411	0,000 0,100 0,200 0,299 0,380 0,446	0,000 0,100 0,200 0,300 0,394 0,472	0,000 0,100 0,200 0,300 0,397 0,482	0,000 0,100 0,200 0,300 0,397 0,486	0,000 0,100 0,200 0,300 0,397 0,486	0,000 0,100 0,200 0,300 0,397 0,486	0,000 0,104 0,208 0,311 0,412 0,511
2,4 2,8 3,2 3,6 4,0	0,461 0,501 0,532 0,558 0,579	0,499 0,542 0,577 0,606 0,630	0,538 0,592 0,637 0,676 0,708	0,556 0,618 0,671 0,717 0,756	0,565 0,635 0,696 0,750 0,796	0,567 0,640 0,707 0,768 0,820	0,567 0,640 0,709 0,772 0,830	0,605 0,687 0,763 0,831 0,892
4,4 4,8 5,2 5,6 6,0	0,596 0,611 0,624 0,635 0,645	0,650 0,668 0,683 0,697 0,708	0,735 0,759 0,780 0,798 0,814	0,789 0,819 0,844 0,867 0,887	0,837 0,873 0,904 0,933 0,958	0,867 0,908 0,948 0,981 1,011	0,833 0,932 0,977 1,018 1,056	0,949 1,001 1,050 1,095 1,138
6,4 6,8 7,2 7,6 8,0	0,653 0,661 0,668 0,674 0,679	0,719 0,728 0,736 0,744 0,751	0,828 0,841 0,852 0,836 0,872	0,904 0,920 0,935 0,948 0,960	0,980 1,000 1,019 1,036 1,051	1,041 1,065 1,088 1,109 1,128	1,090 1,122 1,152 1,180 1,205	1,178 1,215 1,251 1,285 1,316
8,4 8,8 9,2 9,6 10,0 11,0 12,0	0,684 0,689 0,693 0,697 0,700 0,705 0,720	0,757 0,762 0,768 0,772 0,777 0,786 0,794	0,881 0,888 0,896 0,902 0,908 0,922 0,933	0,970 0,980 0,989 0,998 1,005 1,022 1,037	1,065 1,078 1,089 1,100 1,110 1,132 1,151	1,146 1,162 1,178 1,192 1,205 1,223 1,257	1,229 1,251 1,272 1,291 1,309 1,349 1,384	1,347 1,376 1,404 1,431 1,456 1,506 1,550
Примечание. При промежуточных значениях ξ и η коэффициент k определяется по линейной интерполяции

 

Проверяем соблюдение условия:

S ≤ S_u, (2.10.5)

где S – расчетная осадка основания фундамента, рассчитанная по методу линейно-деформируемого слоя, см; S_u - предельная деформация основания, принимаемая по рекомендуемому приложению 4 [6] или приложению 8 настоящего пособия.

Пример расчета

 

Таблица исходных данных

№№ п.п.	Наименование	Един. измерен.	Кол-во
1	2	3	4
1.	Тип фундамента – железобетонный, плитный фундамент мелкого заложения (ФМЗ) при d1/b=3/12=0,25<4	-	3/12<4
2.	Геометрическая форма фундамента – круглый в плане фундамент, диаметром	-	-
3.	Ширина bf или диаметр df фундамента	м	12,00
4.	Глубина заложения подошвы фундамента, d1	м	3,00
5.	Среднее давление на грунт основания под подошвой фундамента (контактное давление), Р	МПа	0,20
В основании фундамента залегают грунты:
6.	Первый слой от уровня подошвы ИГЭ №1
6.1.	Суглинок толщиной, h1	м	4,80
6.2.	Модуль деформации ИГЭ №1, Е1	МПа	15,00
7.	Второй слой от уровня подошвы ИГЭ №2
7.1.	Глина толщиной, h2	м	16,00
7.2.	Модуль деформации ИГЭ №2, Е2	МПа	22,00

 

Схема к расчету осадки методом линейно-деформируемого слоя представлена на рисунке 2.10.2.

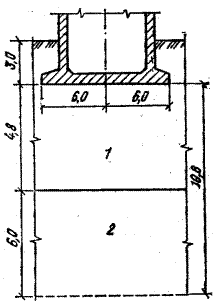
Рис. 2.10.2. Схема к расчету осадки методом линейно-деформируемого слоя

 

Абсолютную осадку круглого в плане фундамента диаметром d_f =12 м >10м, при модуле деформации грунта в основании Е>10 МПа до глубины более 20 м определяем применительно ко второму случаю метода линейно-деформируемого слоя.

Вначале по формуле (2.10.2) определяем мощность сжимаемой толщи Н. Для пылевато-глинистых грунтов (ИГЭ №2), представленных (в настоящем примере) глиной, по таблице 2.10.1 принимаем Н₀=9 м, ψ=0,15. Значение коэффициента k_p=1 принимаем по линейной интерполяции между значениями k_p=0,8 при среднем давлении под подошвой фундамента Р=100 кПа (1 кг/см²) и k_p=1,2 при Р=500 кПа (5 кг/см²). Тогда подставляя значения Н₀, ψ, b, k_p в формулу (2.10.2), определяем толщину Н линейно-деформируемого слоя грунта.

Н=(Н₀+ψ·b)·k_p=(9+0,15·12)·1=10,8 м.

После нахождения расчетной толщины Н грунта определяем величину средней осадки S плитного фундамента круглой в плане формы, расположенного на слое конечной толщины методом линейно-деформируемого слоя. Расчет осадки производим по формуле (2.10.4)

Для этого находим значения коэффициентов k по таблице 2.10.4. Тогда в соответствии со схемой на рисунке 2.10.2:

– для первого слоя (ИГЭ №1), расположенного непосредственно под подошвой плитного фундамента круглой формы в плане на глубине d₁=3,0 м коэффициент k₀=0. На глубине h₁=4,8м ниже подошвы фундамента при ξ₁= = =0,8 в соответствии с графой 2 таблицы 2.10.4 устанавливаем значение коэффициента k₁ =0,18.

– для второго слоя (ИГЭ №2), подстилающего ИГЭ №1 и расположенного под подошвой плитного фундамента круглой формы в плане на глубине 10,8 м при ξ₂= = =1,8 в соответствии с графой 2, таблицы 2.10.4, после линейной интерполяции между значениями ξ=1,6 и ξ=2,0 находим значение коэффициента

k₂= =0,38.

Коэффициент k_m при значениях модулей деформации Е для ИГЭ №1, равном Е₁ =15 МПа>10 МПа, ИГЭ №2, равном Е₂=22 МПа>10 МПа и d_f=12 м>10 м, принимаем по таблице 2.10.3 равным k_m=1,·35. Коэффициент k_c=1,3 принимаем по таблице 2.10.2 при относительной толщине слоя грунта основания

ξ^I= 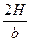= =1,8.

При этих условиях определяем расчетную величину абсолютной осадки методом линейно-деформируемого слоя по формуле (2.10.4)

 

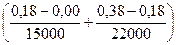= · =0,048≈5 см.

В соответствии с требованиями п.2.39 и предельными деформациями основания рекомендуемого приложения 4 [6] (приложения 8 настоящего пособия) проверяем соблюдение условия S≤S_u (5). В соответствии со схемой на рисунке 2.10.2, принятой для расчета, проектируемое здание может относиться к типам сооружений, отмеченных в п.п. 3-8 приложения 8 настоящего пособия. Предельные деформации основания S_u имеют значения от 10 см до 40 см. Производя сравнение, получаем:

S = 5 см < S_u = 10 - 40 см.

Условие соблюдается, следовательно, фундамент запроектирован верно.

 

2.11. Задача №12. Расчет осадки методом эквивалентного слоя
(метод Н.А. Цытовича)

 

Метод эквивалентного слоя, предложенный Н. А, Цытовичем, дает возможность для многослойных оснований существенно упростить технику расчета конечных осадок и их развития во времени. Этот метод приводит сложную пространственную задачу к эквивалентной, одномерной. По теоретическим предпосылкам он занимает промежуточное положение между строгими аналитическими решениями и методом послойного суммирования [12]. Методом эквивалентного слоя, как считает Н. А. Цытович, можно пользоваться при площади подошвы фундаментов менее 50 м². Это ограничивает возможность использования метода для определения осадки фундаментов с учетом загружения соседних площадей [14].

Основные предпосылки, положенные в основу данного метода:

- -   -

грунт рассматривается как линейно-деформируемая среда; учитывается ограниченное боковое расширение грунтов и жесткость фундаментов; учитываются вес компоненты нормальных напряжений.

Эквивалентным слоем называется такой слой грунта толщиной h_э, осадка которого при сплошной нагрузке Р₀ на поверхности грунта равна осадке грунтового полупространства под воздействием местной нагрузки той же интенсивности.

Толщина эквивалентного слоя h_э грунта зависит от коэффициента Пуассона ν, коэффициента формы площади и жесткости фундамента ω и его ширины b. Толщина эквивалентного слоя h_э грунта рассчитывается по формуле (7.20) [12] или (2.11.1) настоящего пособия

h_э=Aωb, см, (2.11.1)

где Aω –коэффициент эквивалентного слоя грунта, зависящий от коэффициента Пуассона ν для различных грунтов и соотношения сторон загруженной площади η=l/b. Значения Aω приведены в приложении 3 настоящего пособия.

Осадка линейно-деформируемого слоя грунта при сплошной равномерно-распределенной нагрузке рассчитывается по формуле

S=Р₀ ·h_э·m_ν, см, (2.11.2)

где Р₀ – давление по кровле сжимаемого слоя, кПа;

h_э – толщина эквивалентного слоя грунта, с поверхности которого приложена сплошная равномерно-распределенная нагрузка интенсивностью Р₀, см;

m_ν – коэффициент относительной сжимаемости грунта.

Осадку слоистого основания методом эквивалентного слоя вычисляют приближенно. В расчетной схеме сжимаемую толщу грунта, которая практически оказывает влияние на осадку фундамента, принимают в среднем равной двум мощностям эквивалентного слоя: Н_с=2∙h_э, а распределение дополнительных давлений в основании – в виде треугольной эпюры. Вершину треугольной эпюры назначают на глубине, равной Н_с, а основание эпюры, равное Р₀, - под подошвой фундамента (рис. 2.11.1). Грунты, вошедшие в сжимаемую толщу, считают однородными с осредненными характеристиками.

 

Рис. 2.11.1. Схема к расчету осадки методом эквивалентного слоя для слоистого напластования грунтового основания:

1-криволинейная эпюра дополнительных напряжений по оси фундамента; 2-эквивалентная по площади треугольная эпюра с вершиной на глубине 2h_э от уровня подошвы фундамента; z_i-расстояние от середины слоя до глубины 2h

Средний коэффициент относительной сжимаемости m_νm находится из условия, что полная осадка сжимаемой толщи Н_с равна сумме осадок входящих в нее слоев:

m_νm= 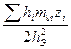, (2.11.3)

где h_i –толщина отдельных слоев грунта до глубины Н_с; m_νi –коэффициент относительной сжимаемости i –го слоя грунта; z_i -расстояние от точки, соответствующей глубине Н_с, до середины рассматриваемого слоя i.

Мощность эквивалентного слоя определяется так же, как и при однородном основании. В предварительных расчетах можно принимать коэффициент Пуассона ν для сжимаемой толщи с преобладанием глинистых грунтов ν=0,3 и с преобладанием песчаных грунтов ν=0,2.

Осадка слоистых оснований методом эквивалентного слоя определяется по формуле S=Р₀ ·h_э·m_ν при замене в ней m_ν на m_νm.

Метод эквивалентного слоя дает хорошие результаты в расчетах фундаментов площадью до 20-30 м² при однородных или слоистых основаниях, в которых сжимаемость отдельных слоев мало отличается друг от друга.

 

Пример расчета

 

Определить методом эквивалентного слоя осадку S ленточного сборного железобетонного фундамента под наружную стену шестиэтажного здания.

 

Таблица исходных данных

№№ п.п.	Наименование	Един. измерен.	Кол-во
1	2	3	4
1.	Тип фундамента – ленточный сборный железобетонный фундамент мелкого заложения (ФМЗ) под наружную стену жилого дома при соотношении d1/b=1,6/1,4=1,143<4	-	<4
2.	Ширина подошвы фундамента bf	м	1,40
3.	Глубина заложения фундамента, h1+d1	м	1,60
4.	Дополнительное давление на грунт основания под подошвой фундамента (контактное давление), Р0= Р–szq0 =220–30=190 кПа	кПа
В основании фундамента залегают грунты:
5.	Первый слой от уровня земли NL, (ИГЭ №1)
	Растительный слой (в качестве основания не пригоден) с удельным весом грунта γII	кН/м3

Окончание таблицы исходных данных

1	2	3	4
6.	Второй слой от уровня земли NL, (ИГЭ №2)
	Песок средней крупности с удельным весом грунта γII=19,1 кН/м3 и модулем деформации Е2	МПа
7.	Третий слой от уровня земли NL, (ИГЭ №3)
	Песок пылеватый с удельным весом грунта γII=19,2 кН/м3 и модулем деформации Е3	МПа
8.	Четвертый слой от уровня земли NL, (ИГЭ №4)
	Супесь с удельным весом грунта γII=19,6 кН/м3 и модулем деформации Е4	МПа
9.	Пятый слой от уровня земли NL, (ИГЭ №5)
	Глина с удельным весом грунта γII=19,6 кН/м3 и модулем деформации Е5	МПа

 

Рис. 2.11.2. Геологический профиль строительной площадки:

1 –растительный слой (γ_II=18 кН/м³); 2 –песок средней крупности; 3 –песок пылеватый; 4 –супесь; 5 –глина; WL=104,05м –уровень подземных вод

 

Схема к расчету осадки методом эквивалентного слоя (метод Н. А. Цытовича) для рассматриваемого примера представлена на рисунке 2.11.3.

Рис. 2.11.3. Схема к расчету осадки методом эквивалентного слоя

(к определению средних коэффициентов относительной сжимаемости)

1. В основании преобладают пески (рис. 2.11.2 и 2.11.3), поэтому по приложению 3 настоящего пособия эквивалентную толщу определяем при ν=0,2, что для средней осадки жесткого фундамента соответствует Аω_m=2,4:

h_э=Aω_m b=2,4·1,4=3,36 м.

2. Толща грунта, практически влияющая на осадку, составит:

Н_С=2 h_э=2·3,36=6,72 м.

При глубине заложения фундамента 1,6 м все грунты входят в эту толщу (рис. 2.11.2).

3. Вычислим значения коэффициентов сжимаемости m_ν каждого слоя в зависимости от модуля деформации Е по формуле

Е= = , отсюда ,

где – безразмерный коэффициент, зависящий от коэффициента Пуассона ν:

для крупнообломочных грунтов (ИГЭ-2)	ν=0,27,	β=0,80
для песков и супесей (ИГЭ-3)…………...	ν=0,30,	β=0,74
для суглинков (ИГЭ-4)…………………...	ν=0,35,	β=0,62
для глин (ИГЭ-5)………………………….	ν=0,41,	β=0,43

 

При модулях деформации Е_i каждого из грунтов (ИГЭ) основания, принятых в соответствии с данными инженерно-геологических изысканий строительной площадки (рис. 2.11.2):

 

№№ ИГЭ	Номер скважины	Глубина отбора образца грунта, м	Наименование грунта	Модуль деформации Е, МПа
ИГЭ-2		1,30	Песок средней крупности	15,0
ИГЭ-3		3,50	Песок пылеватый	5,0
ИГЭ-4		6,00	Супесь	10,0
ИГЭ-5		8,70	Глина	12,0

 

Вычисляем значения коэффициентов сжимаемости m_νi для каждого слоя:

-для ИГЭ-2 (песок средней крупности) β₂ =0,74; 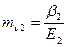= =0,05 МПа^-1;

-для ИГЭ-3 (песок пылеватый) β₃ =0,74; = =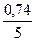0,15 МПа^-1;

-для ИГЭ-4 (супесь) β₄=0,74; = =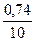0,07 МПа^-1;

-для ИГЭ-5 (глина) β₅=0,43; = =0,04 МПа^-1.

4. Определим средний коэффициент относительной сжимаемости (рис.2.11.3) по формуле

m_νm= =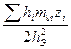

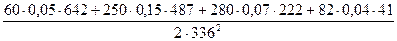= =0,11МПа^-1=0,00011кПа^-1.

5. Средняя осадка фундамента составит:

S=Р₀ ·h_э·m_ν=336·0,00011·190=7 см.

Расчетную величину конечной осадки S=7 см сравниваем с нормативной величиной осадки [S_u]=15 см, рекомендуемой приложением 4 [6] и приложением 8 пособия, для кирпичных зданий:

S=7 см <[S_u]=15 см.

Условие S <[S_u] выполняется, следовательно, принятый в проекте ленточный фундамент шириной b=1,4 м, глубиной заложения 1,6 м, при давлении по подошве Р₀=190 кПа, подобран верно.

ЛИТЕРАТУРА

	Веселов В.А. Проектирование оснований и фундаментов. М.: Стройиздат, 1978. 215 с.
	Далматов Б.И. Механика грунтов, основания и фундаменты. М.: Стройиздат, 1981. 315 с.
	Котов М.Ф. Механика грунтов в примерах. М.: Высшая школа, 1968. 271 с.
	Пешковский Л.М. Расчеты оснований и фундаментов гражданских и промышленных зданий. М.: Высшая школа, 1968. 277 с.
	Пособие по проектированию оснований зданий и сооружений. М.: Стройиздат, 1986. 415 с.
	СНиП 2.02.01 – 83. Строительные нормы и правила. Основания зданий и сооружений. М.: Стройиздат, 1985. – 40 с.
	СН 528-80. Перечень единиц физических величин, подлежащих применению в строительстве. М.: Стройиздат, 1981. 32 с.
	Цытович Н.А. Механика грунтов (краткий курс). М.: Высшая школа, 1983. 288 с.
	Бартоломей А.А. Механика грунтов: Учебник.-М.:АСВ.2003.304с.
	Берлинов М.В. Основания и фундаменты: Учеб. для строит. специальностей вузов. -3-е изд., стер: – М.: Высш. шк., 1999: – 319с.
	СНиП 2.02.03-85. Свайные фундаменты. Нормы проектирования. – М.: ЦИТП Госстроя СССР, 1985. – 42 с.
	Ухов С.Б. и др. Механика грунтов, основания и фундаменты: Учебник/ М., 1994., стр.527.
	Веселов В.А. Проектирование оснований и фундаментов: (основы теории и примеры расчета): Учеб. пособ. для вузов. – 3-е изд., перераб. и доп. – М.: Стройиздат, 1990. – 304 с.: ил.
	Далматов Б.И. Механика грунтов, основания и фундаменты (включая специальный курс инженерной геологии).-2-ое изд. перераб и доп.-Л.: Стройиздат, Ленингр. отд-ние, 1988.–415 с.
	Пилягин А.В. Проектирование оснований и фундаментов зданий и сооружений: Учебное пособие.-М.: Издательтсво Ассоциации строительных вузов, 2005.-248 с.
	СП 50-102-2003. Проектирование и устройство свайных фундаментов. – М: НИИОСП Госстроя России, 2003. – 82с.

ПРИЛОЖЕНИЯ

Приложение 1

Значения коэффициента k для вычисления сжимающих напряжений от
действия сосредоточенной силы в зависимости от отношения r/z

Таблица 1.1

r/z	k	r/z	k	r/z	k	r/z	k
0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,20 0,21 0,22 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49	0,4775 0,4773 0,4770 0,4764 0,4756 0,4745 0,4732 0,4717 0,4699 0,4679 0,4657 0,4633 0,4607 0,4579 0,4548 0,4516 0,4482 0,4446 0,4409 0,4370 0,4329 0,4286 0,4242 0,4197 0,4151 0,4103 0,4054 0,4004 0,3954 0,3902 0,3849 0,3796 0,3742 0,3687 0,3632 0,3577 0,3521 0,3465 0,3408 0,3351 0,3294 0,3238 0,3181 0,3124 0,3068 0,3011 0,2955 0,2899 0,2843 0,2788	0,50 0,51 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71 0,72 0,73 0,74 0,75 0,76 0,77 0,78 0,79 0,80 0,81 0,82 0,83 0,84 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 0,98 0,99	0,2733 0,2679 0,2625 0,2571 0,2518 0,2466 0,2414 0,2663 0,2313 0,2263 0,2214 0,2165 0,2117 0,2070 0,2024 0,1978 0,1934 0,1889 0,1846 0,1804 0,1762 0,1721 0,1681 0,1641 0,1603 0,1565 0,1527 0,1491 0,1455 0,1420 0,1386 0,1353 0,1320 0,1288 0,1257 0,1226 0,1196 0,1166 0,1138 0,1110 0,1083 0,1057 0,1031 0,1005 0,0981 0,0956 0,0933 0,0910 0,0887 0,0865	1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 1,29 1,30 1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49	0,0844 0,0823 0,0803 0,0783 0,0764 0,0744 0,0727 0,0709 0,0691 0,0674 0,0658 0,0641 0,0626 0,0610 0,0595 0,0581 0,0567 0,0553 0,0539 0,0526 0,0513 0,0501 0,0489 0,0477 0,0466 0,0454 0,0443 0,0433 0,0422 0,0412 0,0402 0,0393 0,0384 0,0374 0,0365 0,0357 0,0348 0,0340 0,0332 0,0324 0,0317 0,0309 0,0302 0,0295 0,0288 0,0282 0,0275 0,0269 0,0263 0,0257	1,50 1,51 1,52 1,53 1,54 1,55 1,56 1,57 1,58 1,59 1,60 1,61 1,62 1,63 1,64 1,65 1,66 1,67 1,68 1,69 1,70 1,72 1,74 1,76 1,78 1,80 1,82 1,84 1,86 1,88 1,90 1,92 1,94 1,96 1,98 2,00 2,10 2,20 2,30 2,40 2,50 2,60 2,70 2,80 2,90 3,00 3,50 4,00 4,50 5,00	0,0251 0,0245 0,0240 0,0234 0,0229 0,0224 0,0219 0,0214 0,0209 0,0204 0,0200 0,0195 0,0191 0,0187 0,0183 0,0179 0,0175 0,0171 0,0167 0,0163 0,0160 0,0153 0,0147 0,0141 0,0135 0,0129 0,0124 0,0119 0,0114 0,0109 0,0105 0,0101 0,0097 0,0093 0,0089 0,0085 0,0070 0,0058 0,0048 0,0040 0,0034 0,0029 0,0024 0,0021 0,0017 0,0015 0,0007 0,0004 0,0002 0,0001

Таблица 1.2.

Значения коэффициента k_с.

z/b	значения a/b
	1.2	1.4	1.6	1.8		2.2	2.4	2.6	2.8
0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 3,2 3,4 3,6 3,8 4,0 4,2 4,4 4,6 4,8 5,0 6,0 7,0 8,0 9,0 10,0	0,2500 0,2486 0,2401 0,2229 0,1999 0,1752 0,1516 0,1608 0,1123 0,0969 0,0840 0,0732 0,0642 0,0566 0,0502 0,0447 0,0401 0,0361 0,0326 0,0296 0,0270 0,0247 0,0227 0,0209 0,0193 0,0179 0,0127 0,0094 0,0073 0,0058 0,0047	0,2500 0,2489 0,2420 0,2275 0,2075 0,1851 0,1626 0,1423 0,1241 0,1083 0,0947 0,0832 0,0734 0,0651 0,0580 0,0519 0,0467 0,0421 0,0382 0,0348 0,0318 0,0291 0,0268 0,0247 0,0229 0,0212 0,0151 0,0112 0,0087 0,0069 0,0056	0,2500 0,2490 0,2429 0,2300 0,2120 0,1911 0,1705 0,1508 0,1329 0,1172 0,1034 0,0917 0,0813 0,0725 0,0649 0,0583 0,0526 0,0477 0,0433 0,0395 0,0362 0,0333 0,0306 0,0283 0,0262 0,0243 0,0174 0,0130 0,0101 0,0080 0,0065	0,2500 0,2491 0,2434 0,2315 0,2147 0,1955 0,1758 0,1569 0,1396 0,1241 0,1103 0,0984 0,0879 0,0788 0,0709 0,0640 0,0580 0,0527 0,0480 0,0439 0,0403 0,0371 0,0343 0,0317 0,0294 0,0274 0,0196 0,0147 0,0114 0,0091 0,0074	0,2500 0,2491 0,2437 0,2324 0,2165 0,1981 0,1793 0,1613 0,1445 0,1294 0,1158 0,1039 0,0934 0,0842 0,0761 0,0680 0,0627 0,0571 0,0523 0,0479 0,0441 0,0407 0,0376 0,0348 0,0324 0,0302 0,0218 0,0164 0,0127 0,0102 0,0083	0,2500 0,2491 0,2439 0,2329 0,2176 0,1999 0,1818 0,1644 0,1482 0,1334 0,1202 0,1084 0,0979 0,0887 0,0805 0,0732 0,0668 0,0611 0,0561 0,0516 0,0474 0,0430 0,0407 0,0378 0,0352 0,0328 0,0238 0,0180 0,0140 0,0112 0,0092	0,2500 0,2492 0,2440 0,2333 0,2183 0,2012 0,1836 0,1667 0,1509 0,1365 0,1236 0,1120 0,1016 0,0924 0,0842 0,0769 0,0704 0,0646 0,0594 0,0548 0,0507 0,0469 0,0436 0,0405 0,0378 0,0353 0,0257 0,0195 0,0153 0,0122 0,0100	0,2500 0,2492 0,2441 0,2335 0,2188 0,2020 0,1849 0,1685 0,1530 0,1389 0,1263 0,1149 0,1047 0,0955 0,0875 0,0801 0,0735 0,0677 0,0624 0,0577 0,0535 0,0496 0,0462 0,0432 0,0402 0,0376 0,0276 0,0210 0,0165 0,0132 0,0109	0,2500 0,2492 0,2442 0,2337 0,2192 0,2026 0,1858 0,1696 0,1545 0,1408 0,1284 0,1172 0,1071 0,0981 0,0900 0,0828 0,0762 0,0704 0,0651 0,0603 0,0560 0,05214 0,0485 0,0453 0,0424 0,0307 0,0293 0,0224 0,0176 0,0142 0,0117	0,2500 0,2492 0,2442 0,2338 0,2194 0,2031 0,1865 0,1705 0,1557 0,1423 0,1390 0,1191 0,1092 0,1003 0,0923 0,0851 0,0786 0,0727 0,0674 0,0626 0,0588 0,0543 0,0507 0,0474 0,0444 0,0417 0,0310 0,0238 0,0187 0,0152 0,0125	0,2500 0,2492 0,2442 0,2339 0,2196 0,2034 0,1870 0,1712 0,1567 0,1434 0,1314 0,1205 0,1108 0,1020 0,0942 0,0870 0,0806 0,0747 0,0694 0,0646 0,0603 0,0563 0,0527 0,0493 0,0463 0,0435 0,0325 0,0251 0,0198 0,0161 0,0132

 

 

Окончание таблицы 1.2.

Значения коэффициента k_с.

z/b	Значения a/b
3,2	3,4	3,6	3,8
0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 3,2 3,4 3,6 3,8 4,0 4,2 4,4 4,6 4,8 5,0 6,0 7,0 8,0 9,0 10,0	0,2500 0,2492 0,2443 0,2340 0,2198 0,2037 0,1873 0,1718 0,1574 0,1443 0,1324 0,1218 0,1122 0,1035 0,0957 0,0887 0,0823 0,0765 0,0712 0,0664 0,0620 0,0581 0,0544 0,0510 0,0480 0,0451 0,0340 0,0263 0,0209 0,0169 0,0140	0,2500 0,2492 0,2443 0,2340 0,2199 0,2039 0,1876 0,1722 0,1580 0,1450 0,1332 0,1227 0,1133 0,1047 0,0970 0,0901 0,0838 0,0780 0,0728 0,0680 0,0636 0,0596 0,0560 0,0526 0,0495 0,0466 0,0353 0,0275 0,0219 0,0178 0,0147	0,2500 0,2492 0,2443 0,2341 0,2199 0,2040 0,1878 0,1725 0,1584 0,1455 0,1339 0,1235 0,1142 0,1058 0,0982 0,0913 0,0850 0,0793 0,0741 0,0694 0,0650 0,0610 0,0574 0,0540 0,0509 0,0480 0,0366 0,0286 0,0228 0,0186 0,0154	0,2500 0,2492 0,2443 0,2341 0,2200 0,2041 0,1880 0,1728 0,1587 0,1460 0,1345 0,1242 0,1150 0,1066 0,0991 0,0923 0,0861 0,0804 0,0753 0,0706 0,0663 0,0623 0,0586 0,0553 0,0522 0,0493 0,0377 0,0296 0,0237 0,0194 0,0162	0,2500 0,2492 0,2443 0,2341 0,2200 0,2042 0,1882 0,1730 0,1590 0,1463 0,1350 0,1248 0,1156 0,1073 0,0999 0,0931 0,0870 0,0814 0,0763 0,0717 0,0674 0,0634 0,0597 0,0564 0,0533 0,0504 0,0388 0,0306 0,0246 0,0202 0,0167	0,2500 0,2492 0,2443 0,2342 0,2202 0,2044 0,1885 0,1735 0,1598 0,1474 0,1363 0,1264 0,1175 0,1095 0,1024 0,0959 0,0900 0,0847 0,0799 0,0753 0,0712 0,0674 0,0639 0,0606 0,0576 0,0547 0,0431 0,0346 0,0283 0,0235 0,0198	0,2500 0,2492 0,2443 0,2342 0,2202 0,2045 0,1887 0,1738 0,0601 0,0478 0,1368 0,1271 0,1184 0,1106 0,1036 0,0973 0,0916 0,0864 0,0816 0,0773 0,0733 0,0696 0,0622 0,0630 0,0601 0,0573 0,0460 0,0376 0,0311 0,0262 0,0222	0,2500 0,2492 0,2443 0,2342 0,2202 0,2045 0,1888 0,1739 0,1602 0,1480 0,1371 0,1274 0,1188 0,1111 0,1041 0,0980 0,0923 0,0873 0,0826 0,0784 0,0745 0,0709 0,0676 0,0644 0,0616 0,0589 0,0479 0,0396 0,0332 0,0282 0,0242	0,2500 0,2492 0,2443 0,2342 0,2202 0,2046 0,1888 0,1739 0,1603 0,1481 0,1372 0,1276 0,1190 0,1113 0,1045 0,0983 0,0928 0,0877 0,0832 0,0790 0,0752 0,0716 0,0684 0,0654 0,0626 0,0599 0,0491 0,0411 0,0348 0,0298 0,0258	0,2500 0,2492 0,2443 0,2342 0,2202 0,2046 0,1888 0,1739 0,1604 0,1482 0,1373 0,1277 0,1191 0,1115 0,1047 0,0986 0,0930 0,0880 0,0835 0,0794 0,0756 0,0721 0,0689 0,0659 0,0631 0,0606 0,0500 0,0421 0,0359 0,0310 0,0270	0,2500 0,2492 0,2443 0,2342 0,2202 0,2046 0,1888 0,1740 0,1604 0,1482 0,1374 0,1277 0,1192 0,1116 0,1048 0,0987 0,0933 0,0882 0,0837 0,0796 0,0758 0,0724 0,0692 0,0663 0,0635 0,0610 0,0506 0,0428 0,0367 0,0319 0,0280

 

Таблица 1.3.

Значения коэффициента k_z для определения напряжений в случае действия
равномерно распределенной нагрузки в условиях плоской задачи

z/b	Значения y/b
0,00	0,25	0,50	1,00	1,50	2,00
0,00 0,25 0,50 0,75 1,00 1,25 1,50 1,75 2,00 3,00 4,00 5,00 6,00	1,00 0,96 0,82 0,67 0,55 0,46 0,40 0,35 0,31 0,21 0,16 0,13 0,11	1,00 0,90 0,74 0,61 0,51 0,44 0,38 0,34 0,31 0,21 0,16 0,13 0,10	0,50 0,50 0,48 0,45 0,41 0,37 0,33 0,30 0,28 0,20 0,15 0,12 0,10	0,00 0,02 0,08 0,15 0,19 0,20 0,21 0,20 0,17 0,14 0,12 0,10 -	0,00 0,00 0,02 0,04 0,07 0,10 0,13 0,14 0,13 0,12 0,11 0,10 -	0,00 0,00 0,00 0,02 0,03 0,04 0,07 0,08 0,10 0,10 0,09 - -

Таблица 1.4.

Значения коэффициента для определения величины сжимающих
напряжений при треугольной нагрузке

z/b	Значения y/b
-1,50	-1,00	-0,50	0,00	0,25	0,50	0,75	1,00	1,50	2,00	2,50
0,00 0,25 0,50 0,75 1,00 1,50 2,00 3,00 4,00 5,00 6,00	0,000 0,000 0,002 0,006 0,014 0,020 0,033 0,050 0,051 0,047 0,041	0,000 0,000 0,003 0,016 0,025 0,048 0,061 0,064 0,060 0,052 0,041	0,000 0,001 0,023 0,042 0,061 0,096 0,092 0,080 0,067 0,057 0,050	0,000 0,075 0,127 0,153 0,159 0,145 0,127 0,096 0,075 0,059 0,051	0,250 0,256 0,263 0,248 0,223 0,178 0,146 0,103 0,078 0,062 0,052	0,500 0,480 0,410 0,335 0,275 0,200 0,155 0,104 0,085 0,063 0,053	0,750 0,643 0,477 0,361 0,279 0,202 0,163 0,108 0,082 0,063 0,053	0,500 0,424 0,353 0,293 0,241 0,185 0,153 0,104 0,075 0,065 0,053	0,000 0,015 0,056 0,108 0,129 0,124 0,108 0,090 0,073 0,061 0,050	0,000 0,003 0,017 0,024 0,045 0,062 0,069 0,071 0,060 0,051 0,050	0,000 0,000 0,003 0,009 0,013 0,041 0,050 0,050 0,049 0,047 0,045

 

Приложение 2

Коэффициент при определении осадки

Таблица 2.1

ξ=2z/b	Коэффициент α для фундаментов
круглых	прямоугольных с соотношением сторон равным η=l/b	ленточных (η>10 )
1,0	1,4	1,8	2,4	3,2	5,0
0,0 0,4 0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4 4,8 5,2 5,6 6,0 6,4 6,8 7,2 7,6 8,0 8,4 8,8 9,2 9,6 10,0 10,4 10,8 11,2 11,6 12,0	1,000 0,949 0,756 0,547 0,390 0,285 0,214 0,165 0,130 0,106 0,087 0,073 0,062 0,053 0,046 0,040 0,036 0,031 0,028 0,024 0,022 0,021 0,019 0,017 0,016 0,015 0,014 0,013 0,012 0,011 0,010	1,000 0,960 0,800 0,606 0,449 0,336 0,257 0,201 0,160 0,131 0,108 0,091 0,077 0,067 0,058 0,051 0,045 0,040 0,036 0,032 0,029 0,026 0,024 0,022 0,020 0,019 0,017 0,016 0,015 0,014 0,013	1,000 0,972 0,848 0,682 0,532 0,414 0,325 0,260 0,210 0,173 0,145 0,128 0,105 0,091 0,079 0,070 0,062 0,055 0,049 0,044 0,040 0,037 0,033 0,031 0,028 0,026 0,024 0,022 0,021 0,020 0,018	1,000 0,975 0,866 0,717 0,578 0,463 0,374 0,304 0,251 0,209 0,176 0,150 0,130 0,113 0,099 0,087 0,077 0,064 0,062 0,056 0,051 0,046 0,042 0,039 0,036 0,033 0,031 0,029 0,027 0,025 0,023	1,000 0,976 0,876 0,739 0,612 0,505 0,419 0,349 0,294 0,250 0,214 0,185 0,161 0,141 0,124 0,110 0,099 0,088 0,080 0,072 0,066 0,060 0,055 0,051 0,047 0,043 0,040 0,037 0,035 0,033 0,031	1,000 0,977 0,879 0,749 0,629 0,530 0,449 0,383 0,329 0,285 0,24 Дата: 2016-10-02, просмотров: 375. ⇐ Предыдущая234567891011Следующая ⇒ Материалы представленные на сайте исключительно с целью ознакомления пользователям Интернета и не преследуют коммерческих целей или нарушение авторских прав. © 2018 - 2024