При устройстве фундаментов часто производят отрывку котлованов. Связный грунт может держать откос в пределах некоторой глубины. В таких грунтах иногда можно отрывать траншеи и котлованы с вертикальными стенками без крепления. При дополнительном увлажнении такого грунта дождевыми водами сцепление в нем существенно уменьшается, и тогда вертикальный откос может обрушиться. По этой причине стенки котлованов часто делают с откосами или поддерживают креплениями. Одно из таких поддерживающих креплений – шпунтовые стенки. Они применяются при разработке глубоких котлованов ниже уровня подземных вод, на стесненных площадках (около существующих зданий, сооружений, дорог и т.д.).

Шпунтовые стенки обычно выполняют из металла или дерева. Деревянный шпунт из деревянных досок применяют при неглубоких котлованах (до 5 м), а при более глубоких используют металлические шпунтовые стенки, которые могут быть плоскими или корытного профиля.

Устройство свободностоящих шпунтовых стенок нерационально. В неглубоких котлованах применяют стенки с одной верхней опорой. При расчете шпунтовой стенки необходимо сначала определить глубину забивки стенки, и затем по прочности подобрать толщину стенки. Имеются различные способы расчета шпунтовых стенок. Обычно используется приближенный приём, предложенный профессором Э.К.Якоби – способ "маятника", по которому рассматривают только одну часть стенки. По методу "маятника" предполагается, что стенка может вращаться у верхней опоры под действием активного давления грунта. Этому давлению препятствует отпор грунта снаружи, действующий на забитую часть шпунта.

Пример расчета

Дано: Н = 3 м, s = 4м, γ = 18,0 кН/м³, φ = 30^о, расчетные сопротивления древесины на сжатие и на изгиб: R_сж = 10000 кПа; R_изг= 20000 кПа

Решение

Для того, чтобы стена находилась в равновесии и не опрокидывалась, необходимо выполнение следующего условия: åM_A = 0 → M_опр= M_уд→

E_a× r_a = E_р× r_р (2.6.1)

Здесь Е_а – активное давление грунта на 1 п.м. шпунтовой стенки, определяемое как равнодействующая эпюры активного давления грунта:

, кН, (2.6.2)

, (2.6.3)

Е_р – пассивное давление грунта на 1 п.м. шпунтовой стенки, определяемое как равнодействующая эпюры пассивного давления грунта:

Е_р = , кН, (2.6.4)

, м (2.6.5)

Приравнивая опрокидывающие моменты от пассивного и активного давления грунта и перенося в левую часть нашего равенства все H и h получим соотношение:

(2.6.6)

Пользуясь левой частью соотношения, вычисляем значение k:

.

Для вычисленного значения k методом последовательного приближения подбираем значение h. Задаемся h = 1 м.

Задаемся h = 1,2 м. Тогда

.

Окончательно принимаем h = 1,2 м. Тогда при h = 1,2 м:

Усилие в распорке на 1 п.м. шпунтовой стенки находим из условия равновесия проекций всех сил на горизонтальную ось:

åX = 0 → E_p + N_a – E_a = 0→ N_a = E_a – E_p

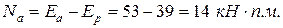
Поскольку по условию задачи распорки установлены с шагом s = 4 м, то итоговое усилие в распорке будет равно:

N_a, _расп = N_a ∙ s = 14 ∙ 4 = 56 кН.

Тогда сечение распорки определим по формуле:

Определим расчетное сечение шпунтовой стенки, соответствующее наибольшему изгибающему моменту в ней от активного давления грунта и реакции в распорке, исходя из того, что максимальный момент по высоте стенки будет находиться на расстоянии y от поверхности земли в точке, где перерезывающая сила Q = 0:

Отсюда:

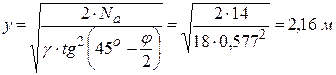
Тогда максимальный изгибающий момент относительно этого сечения определяется по формуле:

.

Требуемый момент сопротивления сечения деревянной шпунтовой стенки:

,

Поскольку 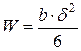, отсюда находим толщину шпунтовой стенки δ ≥ δ_тр:

, принимаем δ = 8 см.

Здесь b = 1 п.м. – ширина стенки.