В учебнике алгебры Ю. Н. Макарычева, Н. Г. Миндюк для 8 класса средней школы (под редакцией С.А. Теляковского) даётся основное свойство дроби следующим образом:
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число , то получится дробь, равная данной.
Основное свойство дроби используется для перемены знаков у членов дроби.
На уроках алгебры в 8 классе учащиеся встречают различные по содержанию упражнения:
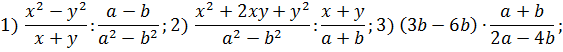
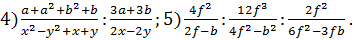
Выполнение именно таких заданий проходит поэтапно. На первом этапе происходит умение распознавать формулы сокращенного умножения, на втором производится само преобразование, использующее формулы − тождества [15].
Школьники на первых порах записывают последовательно каждый шаг преобразований, затем некоторые операции опускают и выполняют устно. Потом учащиеся используют несколько тождеств в решении одного упражнения. Рассмотрим ниже пример:
Упростить выражение: 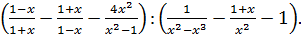
Задания такого типа направлены на то, что бы учащиеся усвоили структуру тождества, а также поняли, что тождество можно как свернуть, так и развернуть (т.е. на обратимость преобразований). Общей целью заданий является углубление понимания тождеств посредством рассмотрения различных упражнений в разных ситуациях, в сочетании с другими темами курса математики.
Существует два подхода при изучении тождественных преобразований дробных рациональных выражений:
1) Алгебраический подход. Состоит в том, что изучаются действия над выражениями. Данный подход не представляется возможным для рассмотрения в школе, потому что для обоснования действий над рациональными выражениями необходимо знание таких понятий, как поле рациональных дробей и кольцо многочленов.
2) Теоретико-функциональный подход. Рассматривается многочлен как целая рациональная функция (одного или нескольких переменных), а алгебраическая дробь как дробно-рациональная функция [13].
Для школьной алгебры эти две позиции полезно объединять, потому что, в первом случае, сосредоточивается внимание учеников на алгебраической стороне вопроса, во втором − представляет интерес функциональная сторона. [13].Методическая схема обучения тождественным преобразованиям дробных рациональных выражений рассмотрена в таблице 2.
| Раздел | Методические приёмы вычислений |
| Дробные рациональные выражения | 1.Приёмы записи преобразований дробных рациональных выражений; 2.Сокращение рациональных дробей; 3.Приведение рациональных дробей к общему знаменателю; 4.Сложение, вычитание умножение и деление рациональных дробей; 5.Возведение рациональной дроби в целую степень; 6.Обобщённый приём упрощения рационального выражения (приведение подобных членов, прибавление и вычитание одного и того же числа); 7.Приёмы доказательства тождества (формулы сокращённого умножения). |
Таблица 2.
Иррациональные выражения
В своём учебном пособии автор Н. Л. Стефанова выделяет следующую цель методики изучения темы содержащих степени и квадратные корни – научить рационально выполнять тождественные преобразования степенных выражений, опирающие на знания свойств степеней [17].
Определение. Если в алгебраическом выражении используется извлечение корня из переменных (или возведение переменных в дробную степень), то его называют иррациональным выражением [18].
Дата: 2019-11-01, просмотров: 470.