В справочных материалах В. А. Гусева рассмотрено следующее определение целых рациональных выражений:

Определение: Целыми рациональными выражениями называются алгебраические выражения, которые не содержат деления на переменные и извлечения корня (возведения в степень с дробным показателем, в частности) [2].

Пример.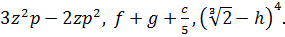

Ранее было рассмотрено понятие тождества, поэтому имеет смысл рассмотреть следующие понятия: область определения алгебраического выражения и допустимые значения переменных.

Определение: Значения переменных, при которых алгебраическое выражение имеет смысл, называют допустимым значением переменных [2].

Определение: Множество всех допустимых значениях переменных называют областью определения алгебраического выражения [11].

Целое рациональное выражение имеет смысл для любого значения переменной. Так, целые рациональные выражения имеют смысл при любых значениях переменных:

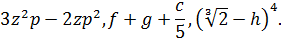
В разделе целые рациональные выражения рассматриваются понятия одночленов и многочленов и действия над ними. В учебнике Ю.Н. Макарычева для 7 класса средней школы (под редакцией С.А. Теляковского) трактуются следующие определения:

Определение. Одночленом называют такое выражение, которое содержит числа, натуральные степени переменных и их произведения и не содержит никаких других действий над числами и переменными. Например,

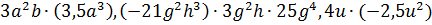 [12].

 Определение. Многочленом называют сумму одночленов. Например,

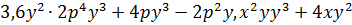 [12].

В своей частной методике В.И. Мишин, при изучении тождественных преобразований целых рациональных выражений, выделяет следующие важные аспекты:

- на множестве одночленов полезно рассматривать лишь одну операцию - умножение;

- не следует рассматривать специально деление многочленов, отнеся его в раздел «рациональные дроби»;

- полезно считать тождественно равными два целых рациональных выражения, значения которых совпадают при одинаковых значениях, входящих в них переменных;

- тождественные преобразования лучше строить на основе законов арифметических действий (аксиом полугруппы и кольца), считать их аксиомами тождественных преобразований [13].

В таблице 1 рассмотрена методическая схема обучения тождественным преобразованиям целых рациональных выражений.

Раздел

Методические приёмы вычислений

Целые рациональные выражения (одночлен, многочлен)

1.Приведение одночленов и многочленов к стандартному виду, выполнение основных действий с целыми рациональными выражениями (раскрытие и заключение в скобки, выполнение арифметических действий); 2.Приёмы разложения многочлена на множители (вынесения общего множителя за скобки, способ группировки); 3.Приёмы доказательства тождества (формулы сокращённого умножения); 4.Специальный приём разложения квадратного трёхчлена на линейные множители, выделения полного квадрата в трёхчлене; 5.Обобщённый приём упрощения целого рационального выражения (приведение подобных членов); 6.Разложение на множители двучлена 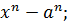7.Возведение двучлена в натуральную степень (бином Ньютона.

Таблица 1.