Введение
В абсолютно каждой области знаний, которая связана с математикой, необходимо заменять одно выражение другим, более простым или более удобным для решения конкретного задания. Иначе говоря, нужно производить тождественные преобразования. Тождественные преобразования являются одной из важнейших линий в школьном курсе алгебры помимо учения о числе, функций, уравнений и неравенств. Данная линия не является отдельной темой в школьном курсе математики, однако, она изучается на протяжении всего курса арифметики, алгебры и начала анализа. Также она присутствует и на уроках геометрии. Простейшие преобразования, которые опираются на арифметические правила, изучаются детьми уже начальной школе. Далее, начиная с 5 класса, школьники также учатся производить тождественные преобразования на основе законов и свойств арифметических действий. Основная нагрузка, направленная на развитие навыков и умений выполнения преобразований, появляется в курсе алгебры 7-9 классов. Как правило, это связано со значительным увеличением числа и различных форм совершаемых преобразований. Культура выполнения, тождественных преобразований развивается так же, как и культура вычислений на основе закреплённых знаний свойств операций и алгоритмов их выполнения. Ребёнок, владеющий ей на высоком уровне, умеет не только правильно обосновать преобразования, но и найти более короткий путь перехода от данного аналитического выражения к окончательному виду преобразований, умеет заметить и проследить за изменением области определения в последовательной цепочке тождественных преобразований, правильно и быстро выполнять преобразования.
Цель курсовой работы: рассмотреть методику изучения тождественных преобразований в курсе алгебры 7-9 классов.
Объект исследования: процесс изучения тождественных преобразований.
Предмет исследования: методика изучения тождественных преобразований в курсе алгебры 7-9 классов.
Для достижения цели были поставлены следующие задачи:
1. Выделить основные понятия линии тождественных преобразований;
2. Провести сравнительный анализ школьных учебников по алгебре;
3. Рассмотреть подклассы математических выражений в курсе алгебры основной школы;
4. Рассмотреть подходы при изучении тождественных преобразований дробных рациональных выражений;
5. Рассмотреть методические схемы обучения тождественным преобразованиям в курсе алгебры основной школы;
Для решения задач были использованы следующие методы исследования: анализ научной, методической литературы, сравнительный анализ школьных учебников по алгебре, обобщение и систематизация полученной информации.
Курсовая работа состоит из введения, двух глав, заключения и списка литературы.
Глава 1.Методические аспекты обучения тождественным преобразованиям в курсе алгебры основной школы
1.1. Основные понятия и содержание линии тождественных преобразований в курсе алгебры основной школы
Тождественные преобразования являются одной из четырёх содержательных линий основных разделов школьного курса алгебры (учение о функции, числе, уравнения и неравенства, тождественные преобразования). Они изучаются, начиная с начальной школы, и имеют своё продолжение в течение всего курса математики. В первом параграфе рассмотрим основные понятия, такие как «выражение», «тождественно равные выражения», «тождество», «тождественные преобразования выражений».
Определение: Выражением в математике называют запись, состоящую из чисел, букв (обозначающих постоянные или переменные величины), знаков математических действий [1].
В школьном курсе математики выделяют два основных класса математических выражений: алгебраические и неалгебраические (трансцендентные).
Определение: Алгебраическим выражением называется выражение, составленное из конечного числа букв и цифр, соединённых знаками действий (сложение, умножение, вычитание, деление, извлечение корня и возведение в целую степень) [2].
Определение: Трансцендентными называются аналитические функции, которые не являются алгебраическими (тригонометрические, логарифмические, показательные) [2].
Можем рассмотреть следующую классификацию выражений (рис 1.):
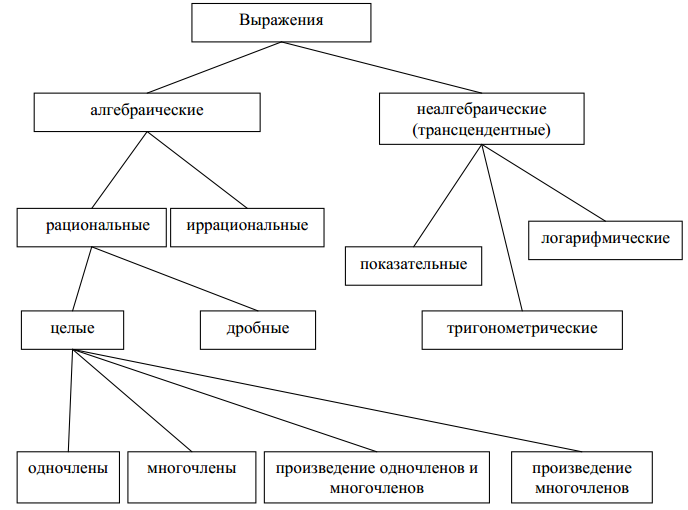
Рис 1.
Линия тождественных преобразований имеет следующее развитие в курсе алгебры основной школы:
5-6 классы: раскрытие скобок, приведение подобных слагаемых, вынесение общего множителя за скобки;
7 класс: тождественные преобразования целых и дробных выражений;
8 класс: тождественные преобразования выражений, содержащих квадратные корни;
9 класс: тождественные преобразования тригонометрических выражений и выражений, содержащих степень с рациональным показателем.
Но стоит заметить, что у разных авторов учебников эта последовательность может отличаться от другой.
Линия тождественных преобразований является одной из важнейших идейных линий школьной математики. Поэтому обучение математики строится таким образом, чтобы учащиеся уже в 5-6 классах получили навыки простейших тождественных преобразований (без употребления термина «тождественные преобразования»). Эти навыки формируются школьниками при выполнении упражнений на приведение подобных слагаемых, раскрытие скобок и заключение в скобки, вынесение множителя за скобки и т. д. Рассматриваются также простейшие преобразования числовых и буквенных выражений. На этом уровне обучения осваиваются преобразования, которые выполняются непосредственно на основе законов и свойств арифметических действий.
Впервые понятие тождества даётся в 7-ом классе. Рассмотрим определение, данное в учебнике А.Г. Мордковича «Алгебра. 7 класс»:
Определение: Тождество – это равенство, верное при любых допустимых значениях, входящих в его состав переменных [3]:
Например: 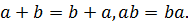
После этого вводится сначала определение тождественно равных выражений:
Определение: Два выражения, соответственные значения которых равны при любых допустимых значениях переменных, называются тождественно равными [3].
В дальнейшем даётся понятие тождественного преобразования выражений:
Определение: Тождественное преобразование выражения – это замена исходного выражения на выражение, тождественно равное ему [3].
В этом определении слово «тождественное» иногда опускают, и говорят просто «преобразование выражения», при этом понимают, что речь идёт о тождественном преобразовании [4].
Приведу примеры для пояснения сформулированного определения:
Пример 1. Данное выражение 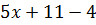 можно заменить тождественно равным ему выражением
можно заменить тождественно равным ему выражением 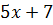 , т.е. эта замена есть тождественное преобразование выражения
, т.е. эта замена есть тождественное преобразование выражения 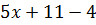 ,
, 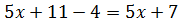 [5].
[5].
Пример 2. Замена выражения 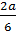 выражением
выражением  является тождественным преобразованием, т.е.
является тождественным преобразованием, т.е. 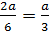 [5].
[5].
Контрпример: Выражение 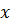 тождественным преобразованием выражения
тождественным преобразованием выражения  не является, так как выражения
не является, так как выражения 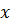 и
и  не тождественно равные [5].
не тождественно равные [5].
В каждой области знаний, в которой так или иначе присутствует математика, появляется необходимость в замене одного выражения другим, более простым или удобным для решения задачи. Иначе говоря, возникает потребность в выполнении тождественных преобразований. Рассмотрим приведённые ниже упражнения:
1.Упростить выражение: 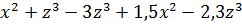
2.Решить уравнение: 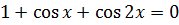
3.Исследуйте функцию: 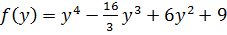
Обязательным условием для решения этих упражнений, отличающихся по содержанию, является предварительное выполнение тождественных преобразований содержащихся в них выражений [4].
В пропедевтическом курсе на уроках математики детьми начинают отрабатываться навыки тождественных преобразований:
а) Приведение подобных слагаемых;
б) Раскрытие и заключение в скобки;
в) Вынесение за скобки общего множителя.
Преобразования такого рода продолжают применять на уроке алгебры в 7 классе при изучении темы: «Многочлены».
Тождества, изучаемые в школе, делятся на 2 этапа:
а) тождества сокращённого умножения и основное свойство дроби;
б) тождества, связывающие основные элементарные функции (показательные, степенные, логарифмические, тригонометрические и др.) и арифметические операции [6].
Выражения и их виды
В школьном курсе математики рассматриваются различные выражения, например: 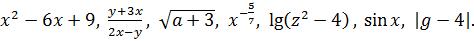
Выражение  содержит операции сложения, вычитания, умножения и деления; выражение
содержит операции сложения, вычитания, умножения и деления; выражение  операции сложения и извлечения квадратного корня;
операции сложения и извлечения квадратного корня; 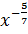 операции возведения в степень с дробным показателем. Выражение
операции возведения в степень с дробным показателем. Выражение 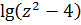 ,кроме действий возведения в степень и вычитания, содержит также знак логарифма; выражение
,кроме действий возведения в степень и вычитания, содержит также знак логарифма; выражение 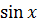 – знак синуса.
– знак синуса.
Выражения, которые не содержат иных действий над переменными, кроме сложения, вычитания, умножения, деления, извлечения корня, возведения в степень с рациональным показателем, называют алгебраическими.
Приведём примеры алгебраических выражений: 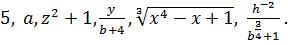
Алгебраические выражения можно разбить на два класса: рациональные и иррациональные. К рациональным относят выражения, которые не содержат других действий над переменными, кроме сложения, вычитания, умножения, деления и возведения в целую степень. К иррациональным выражениям относят все остальные алгебраические выражения, т.е. выражения, содержащие извлечение корня или возведение в степень с дробным показателем.
Примерами рациональных выражений служат: 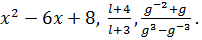
Рациональные выражения тоже в свою очередь можно разбить на два класса: на множество целых выражений и множество дробных. К целым рациональным относят рациональные выражения, которые не содержат деления на выражение с переменными. Дробными считаются те рациональные выражения, которые не являются целыми. Иначе говоря, к дробным выражениям относят такие рациональные выражения, которые содержат деление на выражение с переменными и возведение переменной в степень с отрицательным показателем. Кроме алгебраических в школьном курсе рассматриваются выражения, которые содержат переменные под знаками 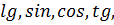 знаком модуля, а также выражения, содержащие операцию возведения в степень с иррациональным показателем. Такие выражения называют неалгебраическими.
знаком модуля, а также выражения, содержащие операцию возведения в степень с иррациональным показателем. Такие выражения называют неалгебраическими.
Заметим, что выражения  хотя и содержат знаки логарифма и синуса, являются алгебраическими, так как под знаком логарифма и под знаком синуса находятся не переменные, а числа. Классификация выражений представлена рисунком 1.
хотя и содержат знаки логарифма и синуса, являются алгебраическими, так как под знаком логарифма и под знаком синуса находятся не переменные, а числа. Классификация выражений представлена рисунком 1.
Проведенная классификация относит то или иное выражение к определенному классу по «внешнему виду», т.е. в зависимости от производимых операций. Эта точка зрения проводится в 4 – 5 классах. А основная нагрузка по формированию умений и навыков выполнения тождественных преобразований лежит на курсе школьной алгебры. Это связано с увеличением числа и разнообразием совершаемых преобразований; с усложнением деятельности по их обоснованию и выяснению условий их применимости; с выделением и изучением обобщенных понятий тождества, равносильного преобразования, тождественного преобразования, логического следования.
2.1.1.1. Этапы освоения применений преобразований формул и буквенно - числовых выражений
Выделяются следующие этапы освоения применений преобразований формул и буквенно-числовых выражений:
Начала алгебры. На этом этапе используется нерасчлененная система преобразований; она представлена правилами выполнения действий над одной или обеими частями формулы. Приведём типичный пример:
Пример 1. Решить уравнение: 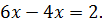 Упростим уравнение, воспользовавшись распределительным законом
Упростим уравнение, воспользовавшись распределительным законом 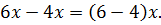 Основанное на этом тождестве тождественное преобразование переводит данное уравнение в равносильное ему уравнение
Основанное на этом тождестве тождественное преобразование переводит данное уравнение в равносильное ему уравнение 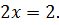
Пример 2. Решить уравнение: 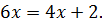 Это уравнение для своего решения требует как тождественного, так и равносильного ему преобразования
Это уравнение для своего решения требует как тождественного, так и равносильного ему преобразования 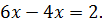 Здесь переносятся члены уравнения из одной части в другую, при этом изменяется знак. Видно, что уже в решении данного задания используется оба типа преобразований – равносильное и тождественное.
Здесь переносятся члены уравнения из одной части в другую, при этом изменяется знак. Видно, что уже в решении данного задания используется оба типа преобразований – равносильное и тождественное.
Цель этого типа – достичь беглости в выполнении заданий на решение простейших уравнений, упрощение формул.
Формирование навыков применения конкретных видов преобразований.
Система правил и приёмов проведения преобразований имеет очень широкую область приложений, то есть изучается на протяжении всего курса математики и используется на этапе начал алгебры. Однако эта система нуждается в дополнительных преобразованиях, которые учитывают особенности структуры преобразуемых выражений. С введения формул сокращенного умножения начинается освоение соответствующих видов преобразований. Далее рассматриваются преобразования, которые связанны с операцией возведения в степень, а так же с различными классами элементарных функций – степенных, показательных, тригонометрических, логарифмических. Каждый из этих типов преобразований должен пройти этап изучения, на котором сосредотачивается внимание на освоении их характерных особенностей.
По мере накопления материала появляется возможность на основе выделения общих особенностей рассматриваемых преобразований ввести понятия тождественного равносильного преобразований.
Преобразования разделяют на два класса: тождественные преобразования как преобразования выражений и равносильные преобразования как преобразования формул. Если возникает потребность упростить одну часть формулы, то в ней выделяется выражение, которое и служит аргументом применяемого тождественного преобразования.
Соответствующий предикат при этом считается неизменным. Например, уравнение 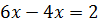 и
и 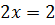 считаются не только равносильными, но и одинаковыми.
считаются не только равносильными, но и одинаковыми.
Организация целостной системы преобразований (синтез).
Основной целью этого этапа, считается формирование гибкого и мощного аппарата, который будет пригоден для использования в решении различных учебных заданий.
Второй этап изучения преобразований разворачивается на протяжении всего курса алгебры неполной средней школы. Переход к третьему этапу происходит при итоговом повторении курса в ходе осмысления уже известного материала усвоенного по частям, по отдельным типам преобразований.
Целостная система преобразований в курсе алгебры и начал анализа, продолжает постепенно совершенствоваться, хотя в основных чертах она уже сформирована. Добавляются новые виды преобразований (относящиеся к тригонометрическим функциям, например), которые обогащают её структуру. Необходимо упомянуть об одном типе преобразований, специфическом для курса алгебры и начал анализа. Это преобразования выражений, которые основаны на правилах дифференцирования и интегрирования; выражений, которые содержат предельные переходы, и преобразования. Рассмотрим основное отличие «алгебраических преобразований» от «аналитических». Оно состоит в характере множества, которое пробегают переменные в тождествах. В алгебраических тождествах переменные пробегают числовые области, а в аналитических этими множествами являются определенные множества функций. Наиболее отчётливо это видно в простейшем примере формулы, выражающей правило дифференцирования суммы: 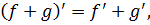 где
где 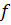 и
и 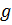 − переменные, пробегающие множество дифференцируемых функций с общей областью определения. Несмотря на то, что отмеченное различие не фиксируется в обучении в курсе алгебры и начала анализа, практика показывает, что рассматриваемые преобразования усваиваются достаточно уверенно; этому способствует их внешнее сходство с преобразованиями алгебраического типа.
− переменные, пробегающие множество дифференцируемых функций с общей областью определения. Несмотря на то, что отмеченное различие не фиксируется в обучении в курсе алгебры и начала анализа, практика показывает, что рассматриваемые преобразования усваиваются достаточно уверенно; этому способствует их внешнее сходство с преобразованиями алгебраического типа.
Иррациональные выражения
В своём учебном пособии автор Н. Л. Стефанова выделяет следующую цель методики изучения темы содержащих степени и квадратные корни – научить рационально выполнять тождественные преобразования степенных выражений, опирающие на знания свойств степеней [17].
Определение. Если в алгебраическом выражении используется извлечение корня из переменных (или возведение переменных в дробную степень), то его называют иррациональным выражением [18].
Заключение
Линия тождественных преобразований является одной из четырёх основных разделов содержательных линий школьного курса алгебры (учение о функции, числе, уравнения и неравенства, тождественные преобразования). Она изучается в течение всего курса математики, начиная с начальных классов.
Школьный курс математики выделяет два основных класса математических выражений: алгебраические и неалгебраические (трансцендентные).
В соответствии с целью и задачами курсовой работы были получены следующие результаты:
1. Рассмотрены основные понятия данной содержательной линии, такие как: «выражение», «тождественно равные выражения», «тождество», «тождественные преобразования выражений»;
2. Проведен сравнительный анализ школьных учебников по алгебре [7], [8], [9], [10], по данной теме;
3. Рассмотрены подклассы математических выражений в курсе алгебры основной школы;
4. Рассмотрены два подхода при изучении тождественных преобразований дробных рациональных выражений (алгебраический подход, теоретико - функциональный подход);
5. Рассмотрены методические схемы обучения тождественным преобразованиям всех видов выражений в курсе алгебры основной школы.
Список используемой литературы
1. Макарычев Ю. Н. Тождественные преобразования многочленов / Ю. Н. Макарычев, Н. Г. Миндюк, К. С. Муравин // Математика в школе. −1973.
2. Методика преподавания математики в средней школе: Частная методика: учеб. пособие для студентов пед. ин-тов по физ.-мат. спец./ А. Я. Блох, В. А. Гусев, Г. В. Дорофеев и др; Сост. В. И. Мишин. −М.: Просвещение, 1987.-Гл.5.−416 с.
3. Мoрдкович А. Г. Алгебра. 7 кл.: в 2 ч. Ч.1: Учеб. для общеобразоват. учреждений / А. Г. Мордкович. − М.: Мнемoзина, 2013. – 240 с.
4. Баум И.В. Тождественные преобразования выражений/ И. В. Баум, Ю. Н.Макарычев ۛ// Преподавание алгебры в 6-8 классах./ Сост. Ю.Н. Макарычев ۛ, Н. Г. Миндюк. − М.: Просвещение, 1980.С. 77-90.
5. Виленкин Н. Я. Равенства, тождества, уравнения, неравенства Н. Я. Виленкин, С. И. Шварцбурд // Математика в школе. - 2000. - № 4.
6. Блох А. Я. О тождественных преобразованиях в курсе алгебры VI-VIII кл.[Текст] / Метод. рекомендации и указания по методике преподавания математики в средней школе: Сб. статей / А. Я. Блох. – М.: МГПИ им. В. И. Ленина, 2005.− 83 с.
7. Алгебра. 7класс: учеб. для общеобразоват. учреждений / А45 [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – М. : Просвещение, 2013. −256 c.
8. Алгебра. 7класс: учеб. для общеобразоват. организаций/ А45 [С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин]. – М. : Просвещение, 2013. −287 c.
9. Алгебра. 7класс: учеб. для общеобразоват. организаций/ А45 [Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович и др.]. – 2-е изд. – М. : Просвещение, 2014. −287 c.
10. Алгебра. 7класс: учеб. для общеобразоват. Учебных заведений/ А45 [А. Г. Мерляк, В.Б. Полонский, М. С. Якир ]. – Х. : Гимназия, 2015. −256 c.
11. Макарычев Ю.Н. и др. Алгебра: Учебник для 8 класса средней школы / Под ред. С.А. Теляковскогоۛ. – М.: Просвещение, 2014.−235 с.
12. Макарычев Ю.Н. и др. Алгебра: Учебник для 7 класса средней школы / Под ред. С.А. Теляковского.— М.: Просвещение, 2014.− 235 с.
13. Методика преподавания математики в средней школе: Частная методика / Сост. В.И. Мишин. — М.: Просвещение, 2003.− 421 с.
14. Мoрдкович А.Г. Алгебра. 8 кл.: учебник для классов с углубленным изучением математики / А.Г. Мордкович. - М.: Мнемозина, 2013. −228 с.
15. Тождественные преобразования выражений. Математика. 8-9 кл./ М.В. Шабанова, О.Л. Безумова, С.Н. Котова и др. – М.: Дрофа. 2010.− 77 с.
16. Федеральный государственный образовательный стандарт общего основного образования. / М-во образования и науки РФ.−М. : Просвещение, 2010. – 50 с.
17. Стефанова Н.Л. , Подходова Н.С. Методика и технология обучения математике. Учеб. пособие / Н.Л. Стефанова и др. – М. : Дрофа, 2008.−416 с.
18. Мордкович А.Г. Алгебра и начала анализа. 9 кл.: в 2 ч. 4.I: Учеб. для общеобразоват. учреждений / А.Г. Мордковичۛ.–М.: Мнемозина, 2013
19. Алимов Ш. А., Колягин Ю. М., Сидоров Ю. В. и др. Алгебра: Пособие для учащихся. − М.: Просвещение, 2014. – 255 с.
20. Мордкович А. Г. Алгебра. 7 класс. Тождества. [Электронный ресурс]/А.Г.Мордкович.−URL: https://docbaza.ru/urok/algebra/07/004/141.html (дата обращения 13.06.2019).
21. Лекция II .Тождественные преобразования в школьном курсе математики. [Электронный ресурс].−URL: https://studme.org/288052/matematika_himiya_fizik/tozhdestvennye_preobrazovaniya_shkolnom_kurse_matematiki (дата обращения 05.06.2019).
22. Епифанова Н. М. Роль и место тождественных преобразований в школьном курсе математики. Пропедевтика тождественных преобразований в 5–6 классах. [Электронный ресурс]/ Н. М. Епифанова. – URL: https://studfiles.net/preview/1619806/page:12/ (дата обращения 05.06.2019).
23. Шаляева Ю. Г. Методика изучения тождественных преобразований в курсе алгебры 7–9 классов. [Электронный ресурс]/ Ю. Г. Шаляева– URL: https://multiurok.ru/files/metodika-izucheniia-tozhdestvennykh-preobrazovanii.html (дата обращения 06.06.2019).
24. Стародубова А. Ю. Тождественные преобразования выражений и методика обучения учащихся их выполнению. [Электронный ресурс]/ А. Ю. Стародубова. – URL: https://works.doklad.ru/view/T7S0hJ6vuEc.html (дата обращения 07.06.2019).
Введение
В абсолютно каждой области знаний, которая связана с математикой, необходимо заменять одно выражение другим, более простым или более удобным для решения конкретного задания. Иначе говоря, нужно производить тождественные преобразования. Тождественные преобразования являются одной из важнейших линий в школьном курсе алгебры помимо учения о числе, функций, уравнений и неравенств. Данная линия не является отдельной темой в школьном курсе математики, однако, она изучается на протяжении всего курса арифметики, алгебры и начала анализа. Также она присутствует и на уроках геометрии. Простейшие преобразования, которые опираются на арифметические правила, изучаются детьми уже начальной школе. Далее, начиная с 5 класса, школьники также учатся производить тождественные преобразования на основе законов и свойств арифметических действий. Основная нагрузка, направленная на развитие навыков и умений выполнения преобразований, появляется в курсе алгебры 7-9 классов. Как правило, это связано со значительным увеличением числа и различных форм совершаемых преобразований. Культура выполнения, тождественных преобразований развивается так же, как и культура вычислений на основе закреплённых знаний свойств операций и алгоритмов их выполнения. Ребёнок, владеющий ей на высоком уровне, умеет не только правильно обосновать преобразования, но и найти более короткий путь перехода от данного аналитического выражения к окончательному виду преобразований, умеет заметить и проследить за изменением области определения в последовательной цепочке тождественных преобразований, правильно и быстро выполнять преобразования.
Цель курсовой работы: рассмотреть методику изучения тождественных преобразований в курсе алгебры 7-9 классов.
Объект исследования: процесс изучения тождественных преобразований.
Предмет исследования: методика изучения тождественных преобразований в курсе алгебры 7-9 классов.
Для достижения цели были поставлены следующие задачи:
1. Выделить основные понятия линии тождественных преобразований;
2. Провести сравнительный анализ школьных учебников по алгебре;
3. Рассмотреть подклассы математических выражений в курсе алгебры основной школы;
4. Рассмотреть подходы при изучении тождественных преобразований дробных рациональных выражений;
5. Рассмотреть методические схемы обучения тождественным преобразованиям в курсе алгебры основной школы;
Для решения задач были использованы следующие методы исследования: анализ научной, методической литературы, сравнительный анализ школьных учебников по алгебре, обобщение и систематизация полученной информации.
Курсовая работа состоит из введения, двух глав, заключения и списка литературы.
Глава 1.Методические аспекты обучения тождественным преобразованиям в курсе алгебры основной школы
1.1. Основные понятия и содержание линии тождественных преобразований в курсе алгебры основной школы
Тождественные преобразования являются одной из четырёх содержательных линий основных разделов школьного курса алгебры (учение о функции, числе, уравнения и неравенства, тождественные преобразования). Они изучаются, начиная с начальной школы, и имеют своё продолжение в течение всего курса математики. В первом параграфе рассмотрим основные понятия, такие как «выражение», «тождественно равные выражения», «тождество», «тождественные преобразования выражений».
Определение: Выражением в математике называют запись, состоящую из чисел, букв (обозначающих постоянные или переменные величины), знаков математических действий [1].
В школьном курсе математики выделяют два основных класса математических выражений: алгебраические и неалгебраические (трансцендентные).
Определение: Алгебраическим выражением называется выражение, составленное из конечного числа букв и цифр, соединённых знаками действий (сложение, умножение, вычитание, деление, извлечение корня и возведение в целую степень) [2].
Определение: Трансцендентными называются аналитические функции, которые не являются алгебраическими (тригонометрические, логарифмические, показательные) [2].
Можем рассмотреть следующую классификацию выражений (рис 1.):

Рис 1.
Линия тождественных преобразований имеет следующее развитие в курсе алгебры основной школы:
5-6 классы: раскрытие скобок, приведение подобных слагаемых, вынесение общего множителя за скобки;
7 класс: тождественные преобразования целых и дробных выражений;
8 класс: тождественные преобразования выражений, содержащих квадратные корни;
9 класс: тождественные преобразования тригонометрических выражений и выражений, содержащих степень с рациональным показателем.
Но стоит заметить, что у разных авторов учебников эта последовательность может отличаться от другой.
Линия тождественных преобразований является одной из важнейших идейных линий школьной математики. Поэтому обучение математики строится таким образом, чтобы учащиеся уже в 5-6 классах получили навыки простейших тождественных преобразований (без употребления термина «тождественные преобразования»). Эти навыки формируются школьниками при выполнении упражнений на приведение подобных слагаемых, раскрытие скобок и заключение в скобки, вынесение множителя за скобки и т. д. Рассматриваются также простейшие преобразования числовых и буквенных выражений. На этом уровне обучения осваиваются преобразования, которые выполняются непосредственно на основе законов и свойств арифметических действий.
Впервые понятие тождества даётся в 7-ом классе. Рассмотрим определение, данное в учебнике А.Г. Мордковича «Алгебра. 7 класс»:
Определение: Тождество – это равенство, верное при любых допустимых значениях, входящих в его состав переменных [3]:
Например: 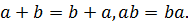
После этого вводится сначала определение тождественно равных выражений:
Определение: Два выражения, соответственные значения которых равны при любых допустимых значениях переменных, называются тождественно равными [3].
В дальнейшем даётся понятие тождественного преобразования выражений:
Определение: Тождественное преобразование выражения – это замена исходного выражения на выражение, тождественно равное ему [3].
В этом определении слово «тождественное» иногда опускают, и говорят просто «преобразование выражения», при этом понимают, что речь идёт о тождественном преобразовании [4].
Приведу примеры для пояснения сформулированного определения:
Пример 1. Данное выражение 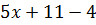 можно заменить тождественно равным ему выражением
можно заменить тождественно равным ему выражением 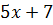 , т.е. эта замена есть тождественное преобразование выражения
, т.е. эта замена есть тождественное преобразование выражения 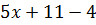 ,
, 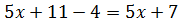 [5].
[5].
Пример 2. Замена выражения 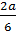 выражением
выражением  является тождественным преобразованием, т.е.
является тождественным преобразованием, т.е. 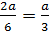 [5].
[5].
Контрпример: Выражение 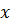 тождественным преобразованием выражения
тождественным преобразованием выражения  не является, так как выражения
не является, так как выражения 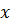 и
и  не тождественно равные [5].
не тождественно равные [5].
В каждой области знаний, в которой так или иначе присутствует математика, появляется необходимость в замене одного выражения другим, более простым или удобным для решения задачи. Иначе говоря, возникает потребность в выполнении тождественных преобразований. Рассмотрим приведённые ниже упражнения:
1.Упростить выражение: 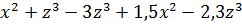
2.Решить уравнение: 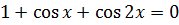
3.Исследуйте функцию: 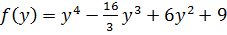
Обязательным условием для решения этих упражнений, отличающихся по содержанию, является предварительное выполнение тождественных преобразований содержащихся в них выражений [4].
В пропедевтическом курсе на уроках математики детьми начинают отрабатываться навыки тождественных преобразований:
а) Приведение подобных слагаемых;
б) Раскрытие и заключение в скобки;
в) Вынесение за скобки общего множителя.
Преобразования такого рода продолжают применять на уроке алгебры в 7 классе при изучении темы: «Многочлены».
Тождества, изучаемые в школе, делятся на 2 этапа:
а) тождества сокращённого умножения и основное свойство дроби;
б) тождества, связывающие основные элементарные функции (показательные, степенные, логарифмические, тригонометрические и др.) и арифметические операции [6].
Сравнительный анализ учебников по алгебре
Проведем анализ теоретического материала по теме «Тождественные преобразования».
Для исследования были рассмотрены учебники алгебры, рекомендованные Министерством Образования и Науки Российской Федерации к применению в образовательном процессе в общеобразовательных учреждениях. Это учебники: Макарычев Ю. Н. и др. «Алгебра. 7 класс» [7]; Никольский С. М. и др. «Алгебра. 7 класс» [8]; Дорофеев Г. В. и др. «Алгебра. 7 класс» [9]; Мерзляк А. Г. и др. «Алгебра. 7 класс» [10].
В учебнике Макарычева «Алгебра. 7 класс» в первой главе параграфа 2 п. 5 «Тождества. Тождественные преобразования выражений» перед тем как перейти к тождественным преобразованиям, автор даёт определение тождественно равных выражений, затем тождеству:
Определение: Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
Пример: Выражения  и
и 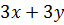 являются тождественно равными, а выражения
являются тождественно равными, а выражения 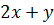 и
и 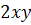 не являются тождественно равными.
не являются тождественно равными.
Пример: Равенство 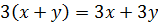 верно при любых значениях
верно при любых значениях 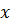 и
и 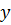 . Такие равенства называются тождествами.
. Такие равенства называются тождествами.
Определение: Равенство, верное при любых значениях переменных называется тождеством. Тождествами считают и верные числовые равенства.
Далее введение понятия тождественного преобразования мотивируется примером:
Чтобы найти значение выражения 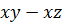 при заданных значениях
при заданных значениях 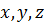 надо выполнить три действия. Например, при
надо выполнить три действия. Например, при 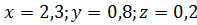 получаем
получаем 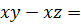
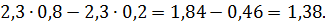
Этот результат можно получить, выполнив лишь два действия, если воспользоваться выражением 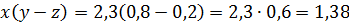
Мы упростили вычисления, заменив выражение 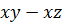 тождественно равным выражением
тождественно равным выражением 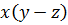 .
.
Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
После того, как автор ввёл понятие «тождественное преобразование», он предлагает вспомнить правила выполнения таких преобразований, как приведение подобных слагаемых, раскрытие скобок, а затем приводит примеры применения таких видов операций:
Пример 1. Приведём подобные слагаемые в сумме 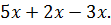 Воспользуемся правилом приведения подобных слагаемых:
Воспользуемся правилом приведения подобных слагаемых: 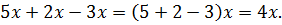 Это преобразование основано на распределительном свойстве умножения.
Это преобразование основано на распределительном свойстве умножения.
Пример 2. Раскроем скобки в выражении 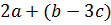 . Применим правило раскрытия скобок, перед которыми стоит знак «плюс»:
. Применим правило раскрытия скобок, перед которыми стоит знак «плюс»: 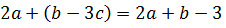 Проведённое преобразование основано на сочетательном свойстве сложения.
Проведённое преобразование основано на сочетательном свойстве сложения.
Пример 3. Раскроем скобки в выражении 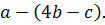 Воспользуемся правилом раскрытия скобок, перед которыми стоит знак «минус»:
Воспользуемся правилом раскрытия скобок, перед которыми стоит знак «минус»:  Выполненное преобразование основано на распределительном свойстве умножения и сочетательном свойстве сложения. Покажем это. Представим в данном выражении второе слагаемое
Выполненное преобразование основано на распределительном свойстве умножения и сочетательном свойстве сложения. Покажем это. Представим в данном выражении второе слагаемое 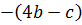 в виде произведения
в виде произведения 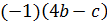 :
: 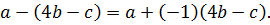 Применив указанные свойства действий, получим
Применив указанные свойства действий, получим 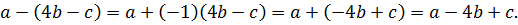
Далее предлагается ответить на вопросы по изученной теме и даны задания на доказательства тождеств.
В учебнике С. М. Никольского, М. К. Потапова, Н. Н. Решетникова, А. В. Шевкина данная тема вводится в главе 2 «Алгебраические выражения», §5 «Многочлены», п. 5.9 «Тождественное равенство целых выражений», а именно приводится пример равенства двух многочленов 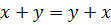 , а затем говорят о том, что если заменить буквы числами, то данное равенство превратится в верное числовое равенство. Сумма чисел не изменится, если в ней поменять местами слагаемые. После этого авторы приходят к выводу, что равенства, получаемые при приведении подобных членов, при умножении одночлена на многочлен, многочлена на многочлен и т.д., также превращаются в верные числовые равенства, если в них заменить буквы числами, формулируют определение тождества:
, а затем говорят о том, что если заменить буквы числами, то данное равенство превратится в верное числовое равенство. Сумма чисел не изменится, если в ней поменять местами слагаемые. После этого авторы приходят к выводу, что равенства, получаемые при приведении подобных членов, при умножении одночлена на многочлен, многочлена на многочлен и т.д., также превращаются в верные числовые равенства, если в них заменить буквы числами, формулируют определение тождества:
Определение: Равенство между буквенными выражениями называют тождеством, если оно превращается в верное числовое равенство при подстановке в него вместо букв любых чисел. Равенство, рассмотренное выше, является тождеством.
Для доказательства тождеств используются изученные ранее свойства одночленов, многочленов и правила действий над ними.
Пример 1. Докажем тождество: 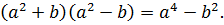
Доказательство. Преобразуем левую часть равенства, применив сначала правило умножения многочленов, затем правило приведения подобных членов: 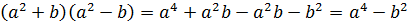 .Следовательно, левая часть равенства равна правой, а это означает, что тождество доказано.
.Следовательно, левая часть равенства равна правой, а это означает, что тождество доказано.
Пример 2. Докажем тождество: 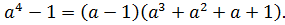
Доказательство. Преобразуем правую часть равенства, применив сначала правило умножения многочленов, затем правило приведения подобных членов: 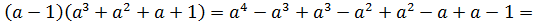
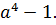 Следовательно, правая часть равенства равна левой, а это означает, что тождество доказано.
Следовательно, правая часть равенства равна левой, а это означает, что тождество доказано.
В этом учебнике также есть замечание, что нулевые многочлены равны нулю тождественно, т.е. при любых числовых значениях входящих в них букв их числовое значение есть нуль. Такими многочленами являются, например: 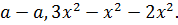
Следующий рассматриваемая нами литература – учебник Дорофеева Г. В. и др. «Алгебра. 7 класс». В п. 3.2. «Преобразование буквенных выражений» главы 3 находится правило: Преобразовать буквенное выражение – это значит заменить его другим выражением, принимающим при любых допустимых значениях букв то же значение, что и исходное. Исходное и преобразованное выражения соединяют знаком «=» и называют тождественно равными или просто равными. Далее авторы предлагают буквенные равенства, выражающие преобразования выражений, считать законами алгебры: 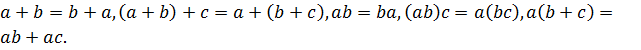 После этого, в этом параграфе рассматриваются правила преобразования сумм и произведений. На основе переместительного и сочетательного законов сложения следует правило: В любой сумме слагаемые можно как угодно переставлять и произвольным образом объединять в группы. Приводится пример: выражение
После этого, в этом параграфе рассматриваются правила преобразования сумм и произведений. На основе переместительного и сочетательного законов сложения следует правило: В любой сумме слагаемые можно как угодно переставлять и произвольным образом объединять в группы. Приводится пример: выражение 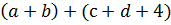 можно записать в виде
можно записать в виде 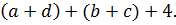
С помощью указанного правила можно преобразовывать не только «чистые суммы », но и смешанные выражения, составленные с помощью знаков «+» и «-» .Далее приводится пример выражения: 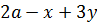 .Так как вычитание всегда можно заменить сложением , то его можно считать суммой выражений
.Так как вычитание всегда можно заменить сложением , то его можно считать суммой выражений  :
: 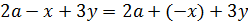 .Меняя каким-либо образом эти слагаемые местами, будем получать равные выражения. Например:
.Меняя каким-либо образом эти слагаемые местами, будем получать равные выражения. Например: 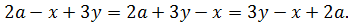 Авторы учебника говорят что такие суммы называются алгебраическими, так как и всегда можно представить в виде суммы, алгебраическими потому, что в исходной записи они все же «чистыми» суммами не являются. После дачи теоретического материала, приводятся примеры упрощения суммы и произведений выражений, а также указаны вопросы для освоения текущей темы. Также присутствуют задания для самостоятельной работы.
Авторы учебника говорят что такие суммы называются алгебраическими, так как и всегда можно представить в виде суммы, алгебраическими потому, что в исходной записи они все же «чистыми» суммами не являются. После дачи теоретического материала, приводятся примеры упрощения суммы и произведений выражений, а также указаны вопросы для освоения текущей темы. Также присутствуют задания для самостоятельной работы.
В учебнике Мерзляка А.Г. и др. «Алгебра. 7 класс» тождествам, также как и в учебнике Макарычева, уделяется целый параграф. В нём авторы сначала рассматривают две пары выражений: 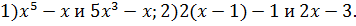 После указаны две таблицы, в которых приведены значения этих выражений при некоторых значениях переменной
После указаны две таблицы, в которых приведены значения этих выражений при некоторых значениях переменной 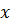 :
:
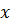
| 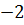
| 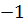
| 
| 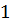
| 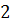
|
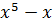
| 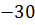
| 
| 
| 
| 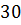
|
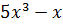
| 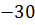
| 
| 
| 
| 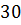
|
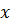
| 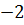
| 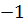
| 
| 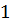
| 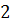
|
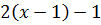
| 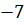
| 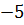
| 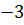
| 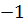
| 1 |
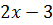
| 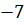
| 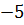
| 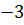
| 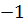
| 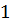
|
После них авторы подчёркивают, что есть значения, которые совпадают для каждой отдельно взятой пары. Вопрос: Сохранится ли подмеченная закономерность при любых других значениях x ?Для выражений, записанных в первой таблице ответ отрицательный, а для второй− положительный.
Доказательство. 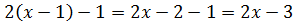 , то есть после упрощения выражение
, то есть после упрощения выражение  превратилось в выражение
превратилось в выражение 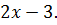 После доказательства формулируется определение тождества:
После доказательства формулируется определение тождества:
Определение. Выражения, соответственные значения которых равны при любых значениях входящих в них переменных, называют тождественно равными.
Примеры тождественно равных выражений:
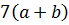 и
и 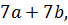 (1)
(1)
 и
и 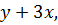 (2)
(2)
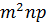 и
и 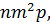 (3)
(3)
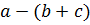 и
и 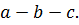 (4)
(4)
После примеров даётся определение тождества:
Определение. Равенство, верное при любых значениях входящих в него переменны, называют тождеством .Из пары тождественно равных выражений легко получить тождество. Например, все равенства (1),(2),(3),(4) являются тождествами.
Затем авторы подчёркивают, что с тождествами учащиеся встречались и раньше: равенства, выражающие свойства сложения и умножения чисел ,являются примерами тождеств. Затем рассматривается пример задания с нахождением значения выражения при определённом значении переменной. Приводятся подобные слагаемые и выражение заменяется тождественно равному ему, после чего значение переменной подставляется в выражение:
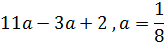
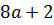
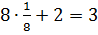
Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения.
Приведение подобных слагаемых и раскрытие скобок – примеры тождественных преобразований выражений. Упрощая выражение, мы фактически заменяем его более простым, тождественно равным ему.
Приводятся методы доказательства тождества:
· Тождественное преобразование одной из частей данного равенств, получая другую часть;
· Тождественное преобразование каждой из частей данного равенства, получая одно и то же выражение;
· Показать, что разность левой и правой частей данного равенства тождественно равна нулю.
Пример 1.Докажите тождество:
1) 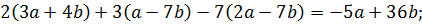
2) 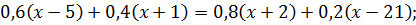
3) 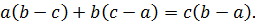
Решение.
1) Упростим левую часть равенства:
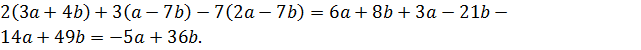 Тождество доказано.
Тождество доказано.
2) Упростим левую и правую части равенства:
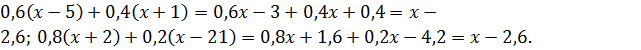
Получили одно и то же выражение. Следовательно, тождество доказано.
3) Рассмотрим разность левой и правой частей:
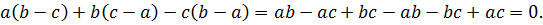 Тождество доказано.
Тождество доказано.
Пример 1. Докажите, что равенство 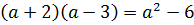 не является тождеством.
не является тождеством.
Решение. Чтобы доказать, что равенство не является тождеством, достаточно привести контрпример: указать такое значение переменной( переменных, если их несколько), при котором данное равенство не выполняется.
Например, при  имеем:
имеем: 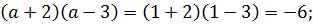
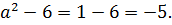 Следовательно, данное равенство не является тождеством.
Следовательно, данное равенство не является тождеством.
Далее ученикам предлагаются вопросы по изучаемой теме и затем даются упражнения для закрепления материала.
В учебнике Ю. Н. Макарычева[7] на изучение в 7 классе темы «Тождественные преобразования выражений» отводится 3 часа, В учебнике C. М. Никольского[8] на изучение в 7 классе этой темы отводится всего лишь 2 часа. В учебниках Г. В. Дорофеева[9] и А. Г. Мерзляка[10] на изучение этой темы отводится также не более 2 часов.
В учебниках Г. В. Дорофеева и А. Г. Мерзляка после ознакомления с темой находятся вопросы, предназначенные для ответов обучающимися на закрепление изученного сразу после теоретического материала и примеров. У С. М. Никольского также это присутствует, но в качестве отдельного упражнения под определённым номером. У Ю. Н. Макарычева вопросы находятся только после практических задач. Практические задания во всех учебниках расположены в конце темы с целью обобщения освоенного. Во всех учебниках перед заданиями, связанными с доказательством тождеств ,есть устные задачи на знания свойств арифметических действий. В учебнике Г. В. Дорофеева присутствует раздел с заданием повышенной сложности, а именно геометрическая задача, которую можно решить с помощью правил алгебры, также в ней есть образец решения подобного рода задачи. В учебнике А. Г. Мерзляка пункт завершается рубрикой «Учимся делать нестандартные вещи». В ней появляется задача, для решения которой нужны не специальные алгебраические знания, а лишь здравый смысл, изобретательность и сообразительность.
Что касается оформления, то, на мой взгляд, учебник Г. В. Дорофеева отличается достаточной красочностью и большим количеством наглядностей.
Проанализировав способы подачи материала в учебниках, можно сделать вывод, что учебник С. М. Никольского не в достаточной мере адаптирован к пониманию материала детьми, излишне академичен, в то время как остальные учебники написаны более простым языком, который не вызывает затруднений при изучении конкретной темы. Такой учебник может хорошо подойти для обучения в классах с углублённым изучением математики. Также в этом учебнике задания для повторения находятся в конце книги, в то время как у Ю. Н. Макарычева и А. Г. Мерзляка такие задания присутствуют в конце каждого пункта. На мой взгляд, учебник Г. В. Дорофеева наилучшим образом подходит для изучения в общеобразовательных организациях, в нём последовательно проводится содержательно методическая линия, включающая комбинаторику, элементы теории вероятностей и статистику, которая органично сочетается с традиционными вопросами курса. Учебник Ю. Н. Макарычева также подходит для основной школы, в нём последовательное изложение теории с привлечением большого числа примеров способствует эффективной организации образовательного процесса. Учебник А. Г. Мерзляка предназначен для углублённого изучения алгебры в профильных классах.
Глава 2.Методика обучения тождественным преобразованиям в курсе алгебры основной школы
2.1. Методическая схема обучения тождественным преобразованиям в курсе алгебры основной школы
Выражения и их виды
В школьном курсе математики рассматриваются различные выражения, например: 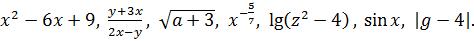
Выражение  содержит операции сложения, вычитания, умножения и деления; выражение
содержит операции сложения, вычитания, умножения и деления; выражение  операции сложения и извлечения квадратного корня;
операции сложения и извлечения квадратного корня; 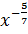 операции возведения в степень с дробным показателем. Выражение
операции возведения в степень с дробным показателем. Выражение 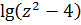 ,кроме действий возведения в степень и вычитания, содержит также знак логарифма; выражение
,кроме действий возведения в степень и вычитания, содержит также знак логарифма; выражение 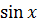 – знак синуса.
– знак синуса.
Выражения, которые не содержат иных действий над переменными, кроме сложения, вычитания, умножения, деления, извлечения корня, возведения в степень с рациональным показателем, называют алгебраическими.
Приведём примеры алгебраических выражений: 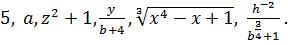
Алгебраические выражения можно разбить на два класса: рациональные и иррациональные. К рациональным относят выражения, которые не содержат других действий над переменными, кроме сложения, вычитания, умножения, деления и возведения в целую степень. К иррациональным выражениям относят все остальные алгебраические выражения, т.е. выражения, содержащие извлечение корня или возведение в степень с дробным показателем.
Примерами рациональных выражений служат: 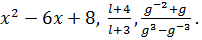
Рациональные выражения тоже в свою очередь можно разбить на два класса: на множество целых выражений и множество дробных. К целым рациональным относят рациональные выражения, которые не содержат деления на выражение с переменными. Дробными считаются те рациональные выражения, которые не являются целыми. Иначе говоря, к дробным выражениям относят такие рациональные выражения, которые содержат деление на выражение с переменными и возведение переменной в степень с отрицательным показателем. Кроме алгебраических в школьном курсе рассматриваются выражения, которые содержат переменные под знаками 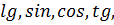 знаком модуля, а также выражения, содержащие операцию возведения в степень с иррациональным показателем. Такие выражения называют неалгебраическими.
знаком модуля, а также выражения, содержащие операцию возведения в степень с иррациональным показателем. Такие выражения называют неалгебраическими.
Заметим, что выражения  хотя и содержат знаки логарифма и синуса, являются алгебраическими, так как под знаком логарифма и под знаком синуса находятся не переменные, а числа. Классификация выражений представлена рисунком 1.
хотя и содержат знаки логарифма и синуса, являются алгебраическими, так как под знаком логарифма и под знаком синуса находятся не переменные, а числа. Классификация выражений представлена рисунком 1.
Проведенная классификация относит то или иное выражение к определенному классу по «внешнему виду», т.е. в зависимости от производимых операций. Эта точка зрения проводится в 4 – 5 классах. А основная нагрузка по формированию умений и навыков выполнения тождественных преобразований лежит на курсе школьной алгебры. Это связано с увеличением числа и разнообразием совершаемых преобразований; с усложнением деятельности по их обоснованию и выяснению условий их применимости; с выделением и изучением обобщенных понятий тождества, равносильного преобразования, тождественного преобразования, логического следования.
2.1.1.1. Этапы освоения применений преобразований формул и буквенно - числовых выражений
Выделяются следующие этапы освоения применений преобразований формул и буквенно-числовых выражений:
Начала алгебры. На этом этапе используется нерасчлененная система преобразований; она представлена правилами выполнения действий над одной или обеими частями формулы. Приведём типичный пример:
Пример 1. Решить уравнение: 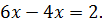 Упростим уравнение, воспользовавшись распределительным законом
Упростим уравнение, воспользовавшись распределительным законом 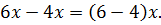 Основанное на этом тождестве тождественное преобразование переводит данное уравнение в равносильное ему уравнение
Основанное на этом тождестве тождественное преобразование переводит данное уравнение в равносильное ему уравнение 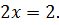
Пример 2. Решить уравнение: 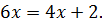 Это уравнение для своего решения требует как тождественного, так и равносильного ему преобразования
Это уравнение для своего решения требует как тождественного, так и равносильного ему преобразования 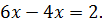 Здесь переносятся члены уравнения из одной части в другую, при этом изменяется знак. Видно, что уже в решении данного задания используется оба типа преобразований – равносильное и тождественное.
Здесь переносятся члены уравнения из одной части в другую, при этом изменяется знак. Видно, что уже в решении данного задания используется оба типа преобразований – равносильное и тождественное.
Цель этого типа – достичь беглости в выполнении заданий на решение простейших уравнений, упрощение формул.
Формирование навыков применения конкретных видов преобразований.
Система правил и приёмов проведения преобразований имеет очень широкую область приложений, то есть изучается на протяжении всего курса математики и используется на этапе начал алгебры. Однако эта система нуждается в дополнительных преобразованиях, которые учитывают особенности структуры преобразуемых выражений. С введения формул сокращенного умножения начинается освоение соответствующих видов преобразований. Далее рассматриваются преобразования, которые связанны с операцией возведения в степень, а так же с различными классами элементарных функций – степенных, показательных, тригонометрических, логарифмических. Каждый из этих типов преобразований должен пройти этап изучения, на котором сосредотачивается внимание на освоении их характерных особенностей.
По мере накопления материала появляется возможность на основе выделения общих особенностей рассматриваемых преобразований ввести понятия тождественного равносильного преобразований.
Преобразования разделяют на два класса: тождественные преобразования как преобразования выражений и равносильные преобразования как преобразования формул. Если возникает потребность упростить одну часть формулы, то в ней выделяется выражение, которое и служит аргументом применяемого тождественного преобразования.
Соответствующий предикат при этом считается неизменным. Например, уравнение 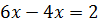 и
и 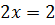 считаются не только равносильными, но и одинаковыми.
считаются не только равносильными, но и одинаковыми.
Организация целостной системы преобразований (синтез).
Основной целью этого этапа, считается формирование гибкого и мощного аппарата, который будет пригоден для использования в решении различных учебных заданий.
Второй этап изучения преобразований разворачивается на протяжении всего курса алгебры неполной средней школы. Переход к третьему этапу происходит при итоговом повторении курса в ходе осмысления уже известного материала усвоенного по частям, по отдельным типам преобразований.
Целостная система преобразований в курсе алгебры и начал анализа, продолжает постепенно совершенствоваться, хотя в основных чертах она уже сформирована. Добавляются новые виды преобразований (относящиеся к тригонометрическим функциям, например), которые обогащают её структуру. Необходимо упомянуть об одном типе преобразований, специфическом для курса алгебры и начал анализа. Это преобразования выражений, которые основаны на правилах дифференцирования и интегрирования; выражений, которые содержат предельные переходы, и преобразования. Рассмотрим основное отличие «алгебраических преобразований» от «аналитических». Оно состоит в характере множества, которое пробегают переменные в тождествах. В алгебраических тождествах переменные пробегают числовые области, а в аналитических этими множествами являются определенные множества функций. Наиболее отчётливо это видно в простейшем примере формулы, выражающей правило дифференцирования суммы: 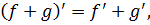 где
где 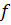 и
и 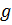 − переменные, пробегающие множество дифференцируемых функций с общей областью определения. Несмотря на то, что отмеченное различие не фиксируется в обучении в курсе алгебры и начала анализа, практика показывает, что рассматриваемые преобразования усваиваются достаточно уверенно; этому способствует их внешнее сходство с преобразованиями алгебраического типа.
− переменные, пробегающие множество дифференцируемых функций с общей областью определения. Несмотря на то, что отмеченное различие не фиксируется в обучении в курсе алгебры и начала анализа, практика показывает, что рассматриваемые преобразования усваиваются достаточно уверенно; этому способствует их внешнее сходство с преобразованиями алгебраического типа.
Дата: 2019-11-01, просмотров: 1235.