1. Идеальные растворы. Физической моделью идеального раствора является совокупность невзаимодействующих частиц, имеющая объем, аддитивно складывающийся из объемов отдельных компонентов. Наиболее важными свойствами идеальных растворов являются: а) Идеальные растворы образуются из чистых компонентов, находящихся в том же агрегатном состоянии, что и раствор, атермально, т.е. без теплового эффекта. б) Объем идеального раствора, образованного из чистых компонентов, находящихся в том же агрегатном состоянии, что и раствор, аддитивно складывается из объемов отдельных компонентов. Основное назначение концепции идеальных растворов – служить эталоном, с которым сравниваются реальные растворы. Все свойства идеальных растворов, в отличие от реальных, легко рассчитываются исходя только из их концентрации и свойств отдельных компонентов.

2. Предельно разбавленные растворы. Предельно разбавленным (п.р.) раствором называют раствор, в котором свойства растворителя практически остались неизменными по сравнению с чистым растворителем ввиду низкой концентрации раствора, в то время как свойства растворенного вещества могут очень сильно отличаться от его свойств в чистом виде ввиду попадания в среду растворителя. Свойствами п.р. растворов обладают обычно все разбавленные растворы вплоть до определенной концентрации, характерной для каждой системы. Чем ближе свойства компонентов, тем до более высокой концентрации сохраняют их растворы свойства п.р. растворов. Для растворов электролитов этот предел очень низок, так как ионы заметно изменяют свойства растворителя уже при миллимолярных концентрациях.

3. Реальные растворы. Различные свойства реальных растворов в той или иной степени отклоняются от идеальных (например, термодинамические). Для адекватного описания этих отклонений обычно требуются различные физические модели, учитывающие межчастичные парные и коллективные взаимодействия, размеры частиц, расстояния между ними и т.д. В некоторых простейших случаях такие модели приводят к результатам, хорошо совпадающим с экспериментом. Однако наиболее универсальный и полностью формальный способ учета неидеальности компонентов раствора был предложен Г. Льюисом в 1907 г., который сохранил ту же форму выражения химического потенциала компонента в реальном растворе, что и в идеальном, но вместо концентрации компонента использовал в нем активности.

По концентрации растворенного вещества растворы можно подразделить на концентрированные (с большой концентрацией растворенного вещества) и разбавленные (с малой концентрацией растворенного вещества).

Важное значение при описании свойств растворов имеет закон Генри: «Масса газа, растворяющегося при постоянной температуре в данном объёме жидкости, прямо пропорциональна парциальному давлению газа». Математически это можно записать так: С=k·р, где k – константа Генри, С – массовая концентрация газа в насыщенном растворе. Важнейшим следствием этого закона является то, что объём газа, растворяющегося при постоянной температуре в данном объёме жидкости, не зависит от его парциального давления.

Коллигативными свойствами раствора называются свойства, зависящие от концентрации частиц растворенного вещества и мало или совсем не зависящие от природы растворителя. К таким свойствам относят:

• давление насыщенного пара растворителя;
• понижение температуры замерзания раствора;
• повышение температуры кипения раствора;
• осмотическое давление.

1. Давление насыщенного пара растворителя. Под давлением насыщенного пара вещества понимают давление его паров в отсутствие других газов, в частности воздуха. Относительное понижение давления пара над раствором равно:

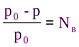, где р₀ – давление насыщенного пара растворителя над чистым растворителем; р - давление насыщенного пара растворителя над раствором; N_в – мольная доля растворенного вещества. Это уравнение является математической формулировкой закона Рауля: «относительное понижение давления насыщенного пара над раствором равно мольной доле растворенного вещества». Явление понижения давления насыщенного пара над раствором вытекает из принципа Ле Шателье.

2. Осмотическое давление. Осмотическое давление - это такое давление, которое нужно приложить к раствору, отделенному от растворителя полупроницаемой перегородкой, чтобы наступило состояние равновесия. Процесс осмоса, в свою очередь, характеризуется самопроизвольным проникновением молекул растворителя через полупроницаемые перегородки.

В 1886 г. Вант-Гофф cформулировал закон (закон Вант-Гоффа), согласно которому «в разбавленном растворе растворенное вещество ведет себя подобно идеальному газу» и показал, что для растворов неэлектролитов невысоких концентраций осмотическое давление Р_ос равно:

Р_ос=С·R·Т=10³·(m/M)·RT, где С= 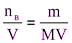– молярность, моль/м³; R=8,31 Дж/(моль·К) – универсальная газовая постоянная; Т – абсолютная температура раствора, К.

Для растворов электролитов величина Р_ос составляет:

Р_ос=i·С·R·Т,

где i – изотонический коэффициент, показывающий, во сколько раз осмотическое давление данного раствора выше нормального. Для каждого раствора этот коэффициент определяется экспериментально.

3. Понижение температуры замерзания раствора (криоскопия). Из всех коллигативных свойств чаще других используются криоскопические измерения ввиду простоты и высокой точности измерения температуры замерзания. Последняя обычно измеряется с помощью специальных метастатических ртутных термометров (термометров Бекмана) с ценой деления 0.01 К. Такие термометры имеют шкалу только на 5 К, но снабжены дополнительным резервуаром для ртути, позволяющим настроить его на любые абсолютные температуры от 260 до 380 К.

Понижение температуры замерзания можно найти как:

Dt_зам=i·К·m, где m – моляльность; К - криоскопическая константа, зависящая только от природы растворителя и не зависящая от природы растворенного вещества. Для воды К=1.86, для бензола К=5,07.

4. Повышение температуры кипения раствора (эбуллиоскопия). Помимо криоскопического метода в химии применяется эбуллиоскопический метод, основанный на измерении температуры кипения растворов.

Повышение температуры кипения можно найти как:

Dt_кип=i·Е·m, где m – моляльность; Е - эбуллиоскопическая константа, зависящая только от природы растворителя и не зависящая от природы растворенного вещества. Для воды Е=0.52, для бензола Е=2,6.

Оба рассмотренные методы позволяют определять молекулярные массы веществ.