Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Все расчеты будут проведены для одного двигателя исходя их тех предположений, что напряжение распределяется по якорным обмоткам равномерно, ток общий, момент- одинаковый. Нагрузка на один двигатель принимается половиной от общей: 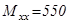 Н*м, 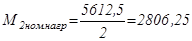 Н*м, номинальная скорость двигателя  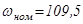рад/с.

Приведем сопротивления к рабочей температуре:

Коэффициент приведения равен:

 

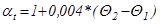; (5.1), ;

 

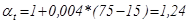где 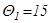⁰ С- температура, при которой дано сопротивление обмоток двигателя в паспортных данных;

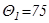⁰ С- рабочая температура двигателя с классом изоляции В.

Сопротивление якорной обмотки без учета падения напряжения на щетках:

 

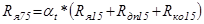; (5.2),  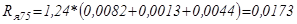Ом;

 

Полное сопротивление якорной цепи двигателя:

 

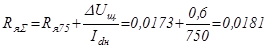 Ом; (5.3)

 

Индуктивность якорной цепи (по формуле Ленвиля-Уманского):

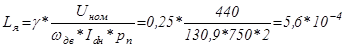 Гн, (5.4)

 

где 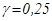- эмпирический коэффициент (при наличии компенсационной обмотки).

Максимальная ЭДС преобразователя:

 

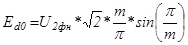; (5.5), ;

 

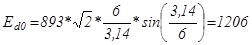Ориентировочно оценим минимальное требуемое значение ЭДС преобразователя, учитывая диапазон :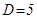

 

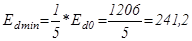; (5.6)

 

Найдем требуемую индуктивность сглаживающего дросселя из условия максимально-допустимых пульсаций тока нагрузки, равных 5%, :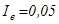

Максимальный (ориентировочно) угол управления:

 

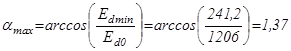 рад; (5.7)

 

Коэффициент для мостовой схемы:

 

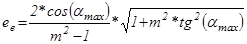; (5.8), ;

 

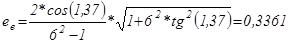Требуемое индуктивное сопротивление сглаживающего дросселя:

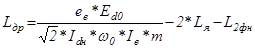; (5.9)

 

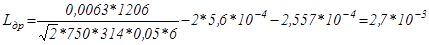 Гн; (5.10)

Выбираем сглаживающий дроссель СРОС3-800МУХЛ4, его паспортные данные:

Номинальный ток дросселя: 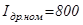 А;

Номинальное сопротивление дросселя: 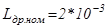 Гн.

Номинальные потери в меди дросселя: 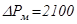 Вт;

Ставим последовательно 2 дросселя: .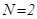

Суммарная индуктивность сглаживающего дросселя:

 

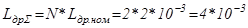 Гн; (5.11)

 

Суммарное активное сопротивление сглаживающего дросселя:

 

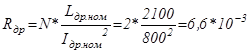 Ом; (5.12)

 

Эквивалентное сопротивление коммутации:

 

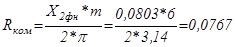 Ом; (5.13)

 

Полное эквивалентное сопротивление якорной цепи одного двигателя:

 

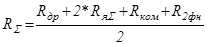; (5.14)

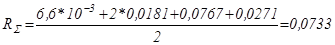 Ом;

Полная индуктивность якорной цепи (учитывая, что вторичная обмотка трансформатора соединена в треугольник и используется мостовая схема, которая "работает" с линейными напряжениями, а, следовательно, ток нагрузки течет только по одной из обмоток трансформатора):

 

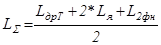; (5.15)

 

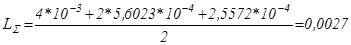 Гн;

Определим конструктивный коэффициент двигателя, связывающий противоЭДС и скорость вращения вала двигателя:

 

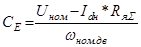; (5.16)

 

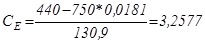 В*с/рад;

Момент на валу, развиваемый электродвигателем:

 

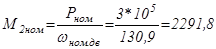 Н*м; (5.17)

 

Электромагнитный момент двигателя:

 

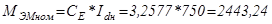 Н*м; (5.18)

 

Найдем относительную разницу между электромагнитным моментом и моментом на валу:

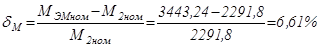; (5.19)

 

Так как разница более 5%, то для дальнейших расчетов найдем конструктивный коэффициент двигателя, связывающий момент на валу двигателя и с током якоря:

 

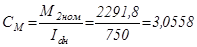 Н*м/А; (5.20)

 

Угол управления при номинальной скорости и номинальной нагрузке:

 

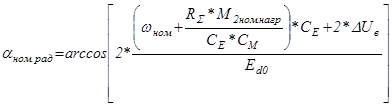; (5.21)

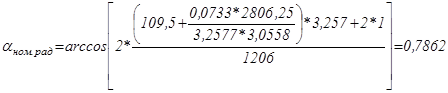рад;

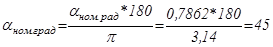^о; (5.22)

 

Угол управления при минимальной скорости и номинальной нагрузке:

 

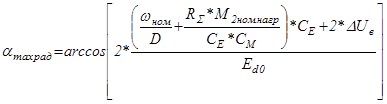; (5.23)

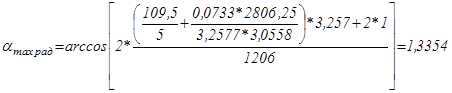рад;

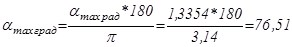^о;

 

Угол управления при номинальной скорости и нагрузке холостого хода:

 

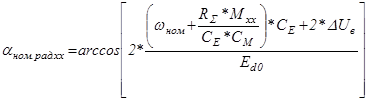; (5.24)

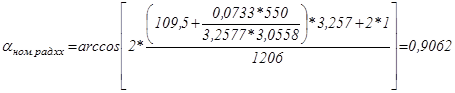 рад;

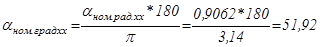^о;

 

Угол управления при минимальной скорости и минимальной нагрузке:

 

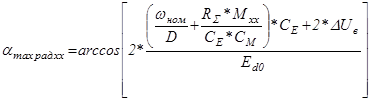; (5.25)

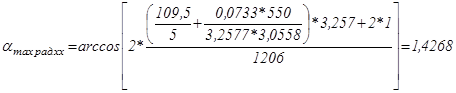 рад;

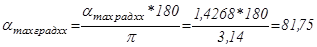^о;

 

Очевидно, что максимальный угол управления в установившемся режиме соответствует 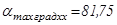 ^о, а минимальный угол управления соответствует 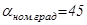^о. Найдем граничные токи и соответственно моменты для двух этих углов:

Для 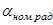 (номинальная скорость и номинальная нагрузка):

 

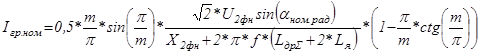; (5.26)

;

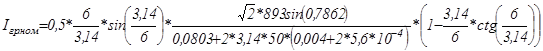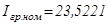 А;

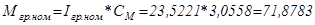 Н*м;

 

Для 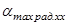 (минимальная скорость, нагрузка холостого хода):

 

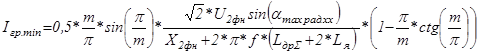; (5.26)

;

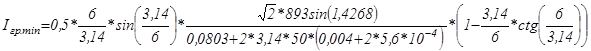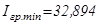 А;

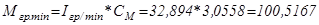 Н*м;

 

Очевидно, что в статике режим прерывистых токов отсутствует при изменении нагрузок и скоростей в пределах, соответствующих заданию.

Далее рассчитаем и построим механические и электромеханические характеристики привода в разомкнутом состоянии:

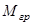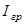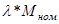Зону непрерывных токов в принципе можно было строить по 2-м точкам (  или ) и (  или 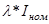) но мы возьмем для наглядность несколько точек.

Зададимся 4-мя значениями момента. . Тогда скорость двигателя для угла управления 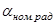 будет равна:

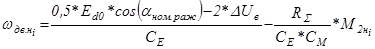; (5.27)

;

;

 

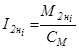Результаты расчетов и графики находятся в приложении А.

Скорость двигателя для угла управления 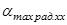 будет равна:

 

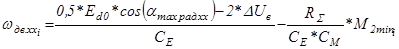; (5.28)

;

;

 

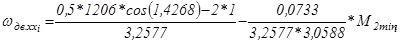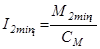Результаты расчетов и графики находятся так же в приложении А.

Зону прерывистых токов рассчитаем так же по точкам. Зададимся 10-ю значениями 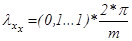. Значения углов занесены в массив 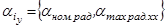Расчеты будут производится для тех же двух углов управления, что и предыдущие. Тогда ток, момент и скорость двигателя в зоне прерывистых токов будут равны:

 

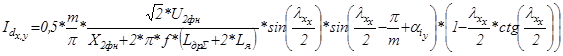; (5.29)

;

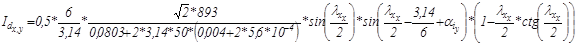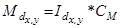; (5.30)

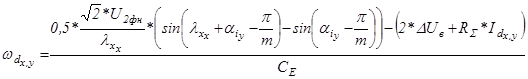; (5.31)

;

 

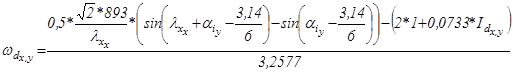Результаты расчетов и графики находятся так же в приложении А.

Характеристики замкнутой системы будут абсолютно жесткие, что будет показано далее.

Говоря по-хорошему, сопротивление 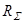 в режиме прерывистых токов меньше сопротивления в режиме непрерывных токов на величину сопротивления коммутации. Однако, в этом случае будет разрыв характеристик в граничной точке. Так же, если говорить точнее, то сопротивление коммутации изменяется с изменением тока нагрузки так же как и эквивалентное сопротивление щеточного контакта. Тогда в режиме непрерывных токов с уменьшение тока нагрузки и становится равным нулю при граничном токе. Однако в этом случае двигатель механическая характеристика двигателя в режиме непрерывных токов становится нелинейной. Следовательно, оставим сопротивления  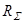одинаковым в режиме прерывистых и непрерывных токов.