Как показывают наблюдения за инновационной деятельностью, распределение результатов инноваций носит характер нормального распределения (см. слайд 7.3).
Нормальное распределение (распределение Гаусса) представляет собой вид распределения случайных величин, с достаточной точностью описывающий распределение плотности вероятности результатов производственно-хозяйственной, финансовой, инновационной деятельности или изменений условий внешней среды, поскольку показатели, характеризующие их, определяются большим числом независимых случайных величин, каждая из которых в отдельности относительно других играет незначительную роль и непредсказуема. Применение нормального распределения для оценки рисков инновационной деятельности также связано с тем, что в основе данных используется, как правило, ряд дискретных значений. Эти теоретические предпосылки, а также апробация моделей для анализа рисков на основе нормального распределения доказывают адекватность этого теоретического инструмента реальным инновационным процессам.
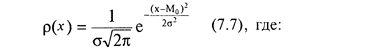
r(х)– плотность вероятности распределения случайной личины х;
s– дисперсия (рассеивание) случайной величины х;
М0– математическое ожидание.
Нормальное распределение позволяет количественно оценить вероятность неблагоприятного значения (см. слайд. 7.4):
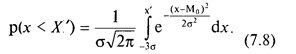
Поскольку основными параметрами нормального распределения являются математическое ожидание и дисперсия, любое их соотношение поддается нормированию, что позволяет применять таблицы стандартизированного нормального распределения к расчету вероятности неблагоприятных значений.
Если применение законов нормального распределения при анализе риска обеспечивает адекватность выводов и оценок, то на практике широко используется такой инструмент как Z-статистика. При анализе результатов инновационной деятельности используют статистические таблицы стандартного нормального распределения (см. Приложение 1), по которым исходя из коэффициента Z, оценивается вероятность того, что результат инновации окажется не хуже некоего критического уровня, определяемого инноватором или инвестором:
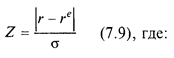
r - критический уровень результата инновации.
По значению Z на основе табличных значений оценивается вероятность риска, если критический уровень превосходит среднее ожидаемое значение:
r > re, если инноватор заинтересован в максимизации результата;
r < re,, если инноватор заинтересован в минимизации результата.
Вероятность того, что результат нововведения превзойдет уровень хуже ожидаемого, оценивается по формуле:
Р=1-р, (7.10), где:
р - значение вероятности, полученное по таблице (Приложение 1).
Вероятность того, что результат реализации инновации компанией из предыдущего примера превысит 15 тыс. руб., можно определить по таблице (Прил. 1), предварительно рассчитав коэффициент Z:
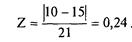
Поскольку критическое значение превосходит ожидаемое значение, а инноватор заинтересован в увеличении прибыли, в таблице указано значение риска:
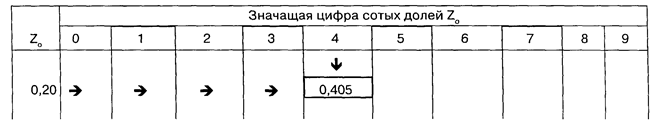
Вероятность того, что доход превысит 15 тыс. руб., составляет 40 %.
Вероятность того, что реализация инновации компанией не принесет ей убытка более 5 тыс. руб., определяется аналогично по табл. (Прил. 1).
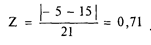
По значению Z в таблице указано значение риска:

Но убыток 5 тыс. руб. – результат хуже ожидаемого (ожидаемая прибыль составляет 10 тыс. руб.). Таким образом, вероятность того, что убыток не превысит 5 тыс. руб., оценивается:
(1 - 0,239) х100% = 66,1%.
Оценка вероятности риска может также производиться с помощью графиков, на которых по оси абсцисс (X) откладываются значения результатов инновации, а по оси ординат (Y) – плотности вероятности получения этих результатов (см. слайд 7.5).
При сравнении вариантов инновационных решений инноватор или инвестор предпочитает либо более высокодоходный вариант (более «правый график»), либо менее рисковый (менее «широкий график») (см. слайды 7.6, 7.7).
Инвестор оценивает 2 инновационных проекта по критерию риска.

Наиболее вероятное значение доходности по проектам:
проект 1: ((-20)х10+(-10)х20+5х30+15х30+20х10):100=4;
проект 2: ((-10)х5+(-5)х20+0х50+5х20+10х5):100 = 0.
Дисперсия доходностей по проектам:
проект 1:
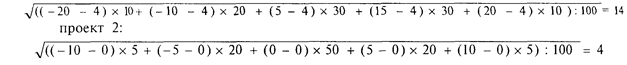
Риск убыточности проектов:
проект 1
Z = (4 - 0) : 14= 0,28 => р = 100 - 39 = 61%;
проект 2
Z = (0 - 0) : 4 = 0,0 => p = 50%.
39% < 50%, следовательно, второй проект сопряжен с меньшим риском.
Степень и цена риска
Риск как экономическая категория совмещает в себе оценку вероятности неблагоприятного развития событий и меру этой неблагоприятности. Поэтому для описания риска используется двухмерная характеристика: степень и цена риска. Степень риска количественно характеризует вероятность неблагоприятной динамики инновационного процесса и негативных результатов инновационной деятельности. Показатель цены риска отражает количественную оценку вероятного результата инновационной деятельности, то есть показывает экономический результат, ради которого инвестор или инноватор пошел на риск.
Финансовому директору АО «Звезда» предстоит выбрать одно из двух альтернативных вложений временно свободных средств предприятия в размере 15 млн. руб.:
• купить государственные ценные бумаги с гарантированной доходностью 3% годовых;
• разместить средства на депозите в коммерческом банке «Слава» под 5 % годовых.
Риск вложений в государственные бумаги составляет 1%, надежность банка оценивается рейтинговым агентством в 90%. Таким образом, степень риска операции с ценными бумагами составляет 1%, а депозитных операций - 10%.
Ожидаемый доход по государственным ценным бумагам за год составит 450 тыс. руб., а по депозитным операциям - 750 тыс. руб.
Цена риска вложений в ценные бумаги составляет:
450 х 0,01 = 4,5 тыс. руб.
Цена риска размещения средств на депозите в банке составляет:
750 х 0,1 =75 тыс. руб.
Вкладывая деньги в банк и стремясь получить более высокий доход, финансовый директор должен иметь в виду, что его ожидаемые потери от этой операции значительно выше, чем от размещения средств в государственных ценных бумагах.
Мера риска
Осуществляемая в процессе принятия управленческих решений экономическая оценка меры риска показывает возможные потери либо в результате какой-либо производственно-хозяйственной или финансовой деятельности, либо вследствие неблагоприятного изменения состояния внешней среды. В зависимости от конкретных условий принятие решения мера риска может оцениваться либо как наиболее ожидаемый негативный результат, либо как пессимистическая оценка возможного результата. Если для описания риска адекватно применение нормального распределения (см. Z-статистика), то мера риска соответственно может оцениваться как математическое ожидание:
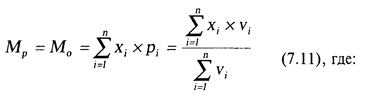
Мр - мера риска;
М0 - наиболее ожидаемый результат (математическое ожидание);
хi - размер потерь в ходе i-го наблюдения;
р i - вероятность возникновения потерь в результате i-го наблюдения;
vi - число случаев наблюдения i-го результата;
п - общее количество наблюдаемых результатов.
При изучении статистики освоения новой продукции были получены следующие данные:
| Группы проектов | Средняя сумма инвестиций, тыс.руб. | Число проектов | Число неудач |
| I IIII | 240 | 12 | 2 |
| II | 400 | 8 | 1 |
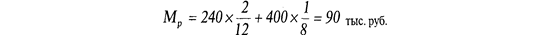
Принимая решение об освоении новой продукции, руководитель предприятия должен быть готов «потерять» в среднем 90 тыс. руб. на каждом новом типе изделий.
Если показатель меры риска используется как пессимистическая оценка результата, то применяется формула максимально возможного негативного отклонения - «три сигмы»:
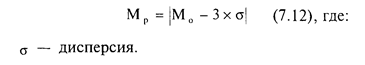
Предварительная оценка результатов инновационного проекта создания консалтингового подразделения аудиторской компании показала, что наиболее ожидаемый доход от этой инновации составит 700 тыс. руб., но точность расчетов (стандартное отклонение, колеблемость) составляет 40%.
Тогда среднее линейное отклонение (s) составляет:
s =700 х 40% : 100% == 280 тыс. руб.
Мера риска в данном случае оценивается как возможный убыток деятельности консалтингового подразделения фирмы:
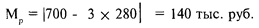
Убыток не превысит 140 тыс. руб.
 Однако мера риска может быть менее М0 – 3 х s , если максимальные потери реально менее расчетного значения. В этом случае мера риска совпадает с максимальными потерями в результате реализации инновационного проекта.
Однако мера риска может быть менее М0 – 3 х s , если максимальные потери реально менее расчетного значения. В этом случае мера риска совпадает с максимальными потерями в результате реализации инновационного проекта.
Мера риска для проекта организации выпуска витаминов (см. выше) - 20 тыс. руб., поскольку именно эту сумму инновационная фирма затратила на исследования и разработки, хотя по расчетам максимальное негативное отклонение составляет:
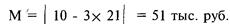
Но такая сумма потерь в данном случае нереальна, поэтому в качестве меры риска принимается размер инвестиций, вложенных в реализацию проекта.
 При принятии решения в области управления риска часто используются кумулятивные статистические кривые (графики Лоренца), на которых накопленным итогом отражается вероятность неблагоприятной ситуации в зависимости от оценки неблагоприятности.
При принятии решения в области управления риска часто используются кумулятивные статистические кривые (графики Лоренца), на которых накопленным итогом отражается вероятность неблагоприятной ситуации в зависимости от оценки неблагоприятности.
Результаты внедрения технологических инноваций на опытном заводе «Пионер» характеризовались следующими данными:
Дата: 2019-11-01, просмотров: 347.