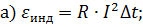 б)
б) 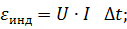
в) 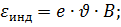 г)
г) 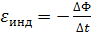 .
.
Ответ: г.
Выберите формулу, верно выражающую величину магнитного потока, пронизывающего контур:
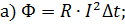 б)
б) 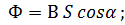
в) 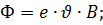 г)
г) 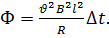
Ответ: б.
Выберите формулу, верно выражающую величину количества теплоты, выделяющегося за время D t на сопротивлении R :
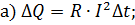 б)
б) 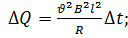
в) 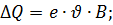 г)
г) 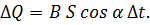
Ответ: а и б.
9. Катушка замкнута на гальванометр. В каких из ниже перечисленных случаях в ней возникает электрический ток?
а) в катушку вдвигается постоянный магнит;
б) в катушку вдвигается другая катушка, меньшего диаметра, по виткам которой течет постоянный ток;
в) вторая катушка, расположенная внутри первой, замыкается на батарею.
Ответ: Во всех трех случаях.
10. Проволочная рамка расположена между полюсами электромагнита так, что плоскость рамки перпендикулярна линиям магнитной индукции. В каких случаях в ней возникает индукционный ток?:
а) при изменении силы тока в обмотках электромагнита;
б) при удалении рамки из зазора между полюсами электромагнита;
в) при повороте рамки относительно оси, лежащей в её плоскости.
Ответ: Во всех трех случаях.
Лабораторная работа 5. Определение величины полной механической энергии гармонических колебаний математического маятника
1. Цель работы − Изучить законы гармонических колебаний, экспериментально получить значение периода, циклической частоты и полной механической энергии гармонических механических колебаний математического маятника.
Приборы и принадлежности
Экспериментальная установка, состоящая из штатива со шкалой, и шарика, подвешенного на невесомой, нерастяжимой нити.
3. Указания к самостоятельной работе
При подготовке к лабораторному занятию необходимо по методическим указаниям к данной лабораторной работе проработать теоретический материал.
.Разобраться с выводом расчетной формулы к данной лабораторной работе.
Подготовиться к ответам на вопросы для тестового контроля к данной лабораторной работе.
Краткие теоретические сведения
Основные понятия и законы
Движения или процессы, характеризуемые определенной повторяемостью во времени, называются колебаниями.
Примеры колебательных процессов: качание маятника часов, переменный электрический ток. В первом случае − при колебательном движении маятника − изменяется координата его центра масс, во втором – сила тока и напряжение в цепи.
В зависимости от физической природы колебаний их разделяют на механические, электромагнитные и другие. Но различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Т.е. целесообразен единый подход к изучению колебаний различной физической природы.
Единый подход к изучению механических и электромагнитных колебаний применялся: английским физиком Д.У. Рэлеем (1842 − 1919 гг.), русским физиком А.Г. Столетовым, русским инженером экспериментатором П.Н. Лебедевым (1866 − 1912 гг.), Л.И. Мандельштамом и его учениками (1879 −1944 гг.).
Колебания называются свободными (собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.
Колебательной системой называется система, совершающая колебания.
Простейшим типом колебаний являются гармонические колебания.
Колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса), называются гармоническими.
Рассмотрение гармонических колебаний важно по двум причинам:
1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;
2) различные периодические процессы можно представить как наложение гармонических колебаний.
Пример математического маятника: небольшой тяжелый шарик, подвешенный на тонкой длинной нити .
Гармонические колебания величины S описываются уравнением:
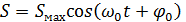
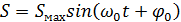
| (1) (2) |
где Smax = A -амплитуда колебания,
wo - круговая (циклическая) частота, собственных (свободных) гармонических колебаний;
jo - начальная фаза колебания в момент времени t = 0 ;
(wot + jo ) - фаза колебания в момент времени t.
Максимальное значение колеблющейся величины, называется амплитудой колебания.
Что определяет фаза колебания?
Фаза колебания определяет значение колеблющейся величины в данный момент времени.
Так как косинус изменяется от +1 до -1 , то S изменяется от +А до -А, или от + Smax до - Smax.
Периодом колебания называется промежуток времени Т, за который фаза получает приращение, равное 2 p .
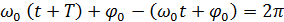
| (3) |
Из соотношения (6.3) вытекает:
| Т = 2p / wo или wo = 2p/Т | (4) (5) |
Запишем еще одно определение периода колебаний:
промежуток времени, за который совершается одно полное колебание, называется периодом колебаний.
В СИ [T] = 1 с ; [wo ] = 1 рад/c = 1 c-1
Частотой колебаний называется число полных колебаний, совершаемых в единицу времени:
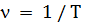
| (6) |
В СИ [ n ] = 1 Гц = 1 с-1
Введем понятия линейной и круговой ( циклической ) частот колебания.
Величина, обратная периоду колебаний, называется линейной частотой колебаний.
1 Гц - частота периодического процесса, при которой за 1 с совершается один цикл процесса.
Сравнивая (4) и (6) получае 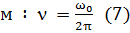 ,
,
wo = 2 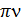 , ( 8) где wo – круговая ( циклическая ) частота колебаний. , ( 8) где wo – круговая ( циклическая ) частота колебаний.
|
Вывод расчетной формулы
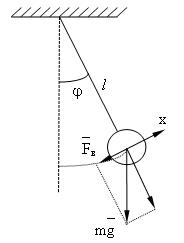 Математическим маятником называется идеализированная система, состоящая из материальной точки, массы m, подвешенной на нерастяжимой невесомой нити и совершающей колебания под действием силы тяжести.
Математическим маятником называется идеализированная система, состоящая из материальной точки, массы m, подвешенной на нерастяжимой невесомой нити и совершающей колебания под действием силы тяжести.
Рис. 1. Математический маятник
Выведем формулу для расчета величины полной механической энергии математического маятника.
Полная механическая энергия маятника складывается из суммы кинетической и потенциальной энергий: 
По определению: 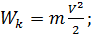
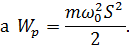
| (10) (11) |
Для нахождения величины полной механической энергии необходимо найти скорость, с которой совершает колебания математический маятник. Величиной совершающей гармонические колебания является величина S – смещение маятника от положения равновесия.
Пусть гармонические колебания маятника совершаются по закону косинуса.
Тогда уравнение гармонических колебаний математического маятника имеет вид:
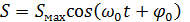 (12)
(12)
Из определения скорости получаем:
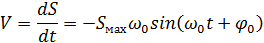
| (13) |
Теперь запишем выражение для кинетической энергии гармонических колебаний математического маятника:
: 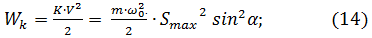
По определению величина потенциальной энергии гармонических колебаний маятника равна 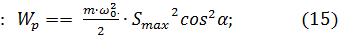 :
:
Запишем выражения полной энергии материальной точки.
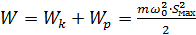 + +
| (16) |
Так как m = const, wо = const, Smax = const, то из соотношения (16) следует вывод:
Дата: 2019-11-01, просмотров: 291.