Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.
Магнитным потоком Φ через площадь S контура называют величину:
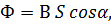
| (5.1) |
где B – модуль вектора магнитной индукции, α – угол между вектором 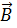 и нормалью
и нормалью 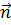 к плоскости контура (рис. 5.1.).
к плоскости контура (рис. 5.1.).
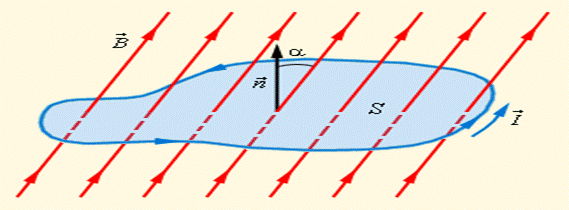
|
Рис. 5. 1. Магнитный поток через замкнутый контур. Направление нормали 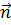 и выбранное положительное направление обхода контура связаны правилом правого буравчика и выбранное положительное направление обхода контура связаны правилом правого буравчика
|
Единица магнитного потока в СИ называется вебер (Вб).
Магнитный поток в 1 Вб , создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2:
1Вб=1 Тл ·м2.
М. Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции εинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
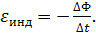
| (5.2) |
Эта формула выражает закон электромагнитной индукции Фарадея.
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Это утверждение, сформулированное в 1833 г., называется правилом Ленца.
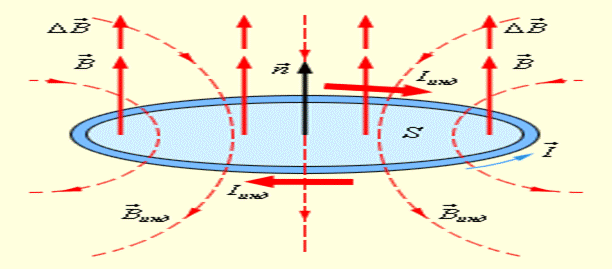
Рис. 5.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.
|
Рис. 5.2. Иллюстрация правила Ленца. В этом примере 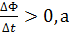 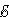 инд < 0.
Индукционный ток Iинд течет навстречу выбранному положительному направлению инд < 0.
Индукционный ток Iинд течет навстречу выбранному положительному направлению 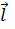 обхода контура обхода контура
|
Правило Ленца отражает тот экспериментальный факт, что 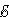 инд и
инд и 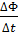 всегда имеют противоположные знаки (знак «минус» в формуле Фарадея).
всегда имеют противоположные знаки (знак «минус» в формуле Фарадея).
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.
1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. C ила Лоренца играет в этом случае роль сторонней силы.
Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле 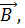 перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью
перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью 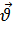 по двум другим сторонам (рис. 5.3).
по двум другим сторонам (рис. 5.3).
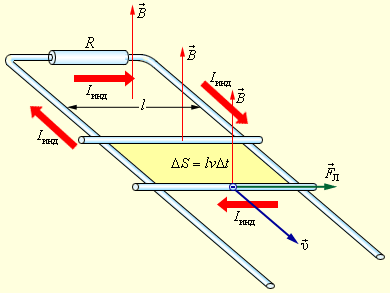
| ||
| Рис. 5.3. Возникновение ЭДС индукции в движущемся проводнике. Указана составляющая силы Лоренца, действующей на свободный электрон | ||
На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью 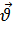 зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 5.3. Она играет роль сторонней силы. Ее модуль равен:
зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 5.3. Она играет роль сторонней силы. Ее модуль равен:
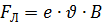 . .
| (5.3) |
Работа силы FЛ на пути l равна:
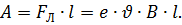
| (5.4) |
По определению ЭДС :
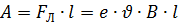 . .
| (5.5) |
В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для 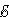 инд можно придать привычный вид. За время Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,
инд можно придать привычный вид. За время Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,
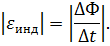
| (5.6) |
Для того, чтобы установить знак в формуле, связывающей 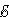 инд и
инд и 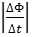 нужно выбрать согласованные между собой по правилу правого буравчика направление нормали
нужно выбрать согласованные между собой по правилу правого буравчика направление нормали 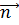 и положительное направление обхода контура
и положительное направление обхода контура 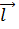 как это сделано на рис. 5.1 и 5.2. Если это сделать, то легко прийти к формуле Фарадея.
как это сделано на рис. 5.1 и 5.2. Если это сделать, то легко прийти к формуле Фарадея.
Если сопротивление всей цепи равно R, то по ней будет протекать индукционный ток, равный Iинд = 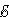 инд/R.
инд/R.
За время Δt на сопротивлении R выделится джоулево тепло:
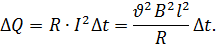
| (5.7) |
Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает!
Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера 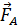 . Для случая, изображенного на рис. 5.3, модуль силы Ампера равен FA = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна:
. Для случая, изображенного на рис. 5.3, модуль силы Ампера равен FA = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна:
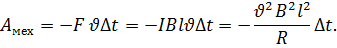
| (5.8) |
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение.
Полная работа силы Лоренца равна нулю. Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 г.
Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления электромагнитной индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
В обоих случаях в замкнутом контуре, пронизываемом линиями вектора В возникает индукционный ток.
Для определения направления индукционного тока необходимо:
1. Определить направление вектора магнитной индукции поля. пронизывающего замкнутый контур. - 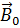 .
.
2. Определить скорость изменения магнитного потока, сцепленного с замкнутым контуром.
Если 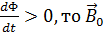 и
и 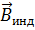 сонаправлены.
сонаправлены.
Если 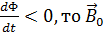 и
и 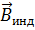 противо направлены.
противо направлены.
3. Зная направление 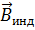 по правилу правого винта определить направление индукционного тока в контуре.
по правилу правого винта определить направление индукционного тока в контуре.
Контрольные вопросы
1. Что такое магнитный поток?
2. В каких единицах в системе СИ измеряется магнитный поток?
3. Сформулируйте закон электромагнитной индукции Фарадея.
4. Вследствие каких причин может изменяться магнитный поток, пронизывающий замкнутый проводящий контур?
5. Какова роль силы Лоренца при движении проводника в магнитном поле?
6. Что называют вихревым магнитным полем?
7. Каковы условия возникновения вихревого магнитного поля?
8. Сформулируйте правило Ленца для определения направления индукционного тока.
9. В каком году и кем было открыто явление электромагнитной индукции?
10. Что обозначает знак минус в законе Фарадея (формула (5.2))?
11. Каков физический смысл правила Ленца?
12. В каких единицах в системе СИ измеряется ЭДС электромагнитной индукции?
Содержание отчета
1. Титульный лист.
2. Цель работы.
3. Приборы и принадлежности.
4. Схема (рисунок) экспериментальной установки с указанием ее основных частей.
5. Определение направления индукционного тока в замкнутом контуре ( сделать рисунки) в двух случаях: ф)приближение к неподвижному контуру полосового магнита северным полюсом; Вывод.
Тест для самоконтроля
1. Магнитным потоком Φ через площадь S контура называется величина, равная:
а) произведению модуля вектора магнитной индукции на площадь контура и синус угла 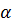 между вектором
между вектором 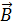 и нормалью
и нормалью 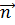 к плоскости контура;
к плоскости контура;
б) произведению модуля вектора магнитной индукции на площадь контура и косинус угла 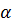 между вектором
между вектором 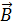 и нормалью
и нормалью 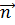 к плоскости контура;
к плоскости контура;
в) произведению модуля вектора магнитной индукции на площадь контура;
г) произведению модуля вектора магнитной индукции на площадь контура и тангенс угла α  между вектором
между вектором 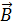 и нормалью
и нормалью 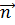 к плоскости контура.
к плоскости контура.
Ответ: б.
2. Явлением электромагнитной индукции называется явление:
а) изменения магнитного потока сцепленного с контуром;
б) возникновения силы Лоренца, действующей на заряженную частицу, движущуюся в магнитном поле;
в) возникновения электрического тока в замкнутом проводящем контуре при изменении времени магнитного потока, пронизывающего контур;
г) возникновения силы Ампера, действующей на проводник с током, помещенный в магнитное поле.
Ответ: в.
Правило Ленца утверждает
а) при изменении магнитного потока в проводящем контуре возникает ЭДС индукции, равная скорости изменения магнитного потока через поверхность, ограниченную контуром;
б) изменение магнитного потока, пронизывающего контур, может происходить вследствие перемещения контура или его частей в постоянном во времени магнитном поле;
в) изменение магнитного потока, пронизывающего контур, может происходить вследствие изменения во времени магнитного поля при неподвижном контуре;
г) индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Ответ: г.
4. Единицей измерения магнитного потока в СИ является:
а) Тл; б) 1 Вб; в) 1 В; г) 1 А.
Ответ: б.
5. Единицей измерения ЭДС электромагнитной индукции в системе СИ является:
а) Тл; б) 1 Вб; в) 1 В; г) 1 А.
Ответ: в.
Дата: 2019-11-01, просмотров: 266.