Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Институт математики, физики и информационных технологий

Кафедра «Общая и теоретическая физика»

Студент ______________________     Группа _______________

Лабораторная работа № 4

« Определение направления индукционного тока в катушке»

Тольятти 2019

Лабораторная работа №4. Определение направления индукционного тока в катушке

Содержание отчета

1. Титульный лист.

2. Цель работы.

3. Приборы и принадлежности.

4. Схема (рисунок) экспериментальной установки с указанием ее основных частей.

5.  Определение направления индукционного тока в замкнутом контуре ( сделать рисунки) в двух случаях: ф)приближение к неподвижному контуру полосового магнита северным полюсом;        Вывод.

 

Тест для самоконтроля

1. Магнитным потоком Φ через площадь S контура называется величина, равная:

а) произведению модуля вектора магнитной индукции на площадь контура и синус угла 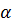между вектором  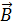и нормалью  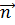 к плоскости контура;

б) произведению модуля вектора магнитной индукции на площадь контура и косинус угла 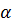между вектором  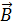 и нормалью  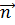 к плоскости контура;

в) произведению модуля вектора магнитной индукции на площадь контура;

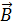г) произведению модуля вектора магнитной индукции на площадь контура и тангенс угла α между вектором  и нормалью  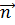 к плоскости контура.

Ответ: б.

2. Явлением электромагнитной индукции называется явление:

а) изменения магнитного потока сцепленного с контуром;

б) возникновения силы Лоренца, действующей на заряженную частицу, движущуюся в магнитном поле;

в) возникновения электрического тока в замкнутом проводящем контуре при изменении времени магнитного потока, пронизывающего контур;

г) возникновения силы Ампера, действующей на проводник с током, помещенный в магнитное поле.

Ответ: в.

Правило Ленца утверждает

а) при изменении магнитного потока в проводящем контуре возникает ЭДС индукции, равная скорости изменения магнитного потока через поверхность, ограниченную контуром;

б) изменение магнитного потока, пронизывающего контур, может происходить вследствие перемещения контура или его частей в постоянном во времени магнитном поле;

в) изменение магнитного потока, пронизывающего контур, может происходить вследствие изменения во времени магнитного поля при неподвижном контуре;

г) индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Ответ: г.

 

4. Единицей измерения магнитного потока в СИ является:

а) Тл; б) 1 Вб; в)   1 В; г) 1 А.

Ответ: б.

5. Единицей измерения ЭДС электромагнитной индукции в системе СИ является:

а) Тл; б) 1 Вб; в)   1 В; г) 1 А.

Ответ: в.

Приборы и принадлежности

Экспериментальная установка, состоящая из штатива со шкалой, и шарика, подвешенного на невесомой, нерастяжимой нити.

3. Указания к самостоятельной работе

При подготовке к лабораторному занятию необходимо по методическим указаниям к данной лабораторной работе проработать  теоретический материал.

.Разобраться с выводом расчетной формулы к данной лабораторной работе.

Подготовиться к ответам на вопросы для тестового контроля к данной лабораторной работе.

Основные понятия и законы

Движения или процессы, характеризуемые определенной повторяемостью во времени, называются  колебаниями.

    Примеры колебательных процессов: качание маятника часов, переменный электрический ток. В первом случае − при колебательном движении маятника − изменяется координата его центра масс, во втором – сила тока и напряжение в цепи.

    В зависимости от физической природы колебаний  их разделяют на  механические, электромагнитные   и другие. Но различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Т.е. целесообразен единый подход к  изучению колебаний различной физической природы.

    Единый подход к изучению механических и электромагнитных колебаний применялся:   английским физиком Д.У. Рэлеем (1842 − 1919 гг.), русским физиком А.Г. Столетовым, русским инженером экспериментатором П.Н. Лебедевым (1866 − 1912 гг.), Л.И. Мандельштамом и его учениками (1879 −1944 гг.).

    Колебания называются свободными (собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

    Колебательной системой называется система, совершающая колебания.

    Простейшим типом колебаний являются гармонические колебания.

    Колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса), называются гармоническими.

    Рассмотрение гармонических колебаний важно по двум причинам:

1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;

2) различные периодические процессы можно представить как наложение гармонических колебаний.

Пример математического маятника: небольшой тяжелый шарик, подвешенный на тонкой длинной нити .

    Гармонические колебания величины S описываются уравнением:

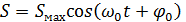
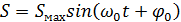
(1) (2)

где S_max = A -амплитуда колебания,

w_o - круговая (циклическая) частота, собственных (свободных) гармонических колебаний;

j_o   - начальная фаза колебания в момент времени t = 0 ;

(w_ot + j_o ) - фаза колебания в момент времени t.

Максимальное значение колеблющейся величины, называется амплитудой колебания.

Что определяет фаза колебания?   

Фаза колебания определяет значение колеблющейся величины в данный момент времени. 

Так как косинус изменяется от +1 до -1 , то S изменяется от +А до -А, или от + S_max до - S_max.

    Периодом колебания называется промежуток времени Т, за который фаза     получает приращение, равное 2 p .

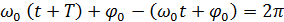
(3)

  Из соотношения (6.3) вытекает:

Т = 2p / wo или wo = 2p/Т

(4) (5)

 Запишем еще одно определение периода колебаний:

    промежуток времени, за который совершается одно полное колебание,  называется периодом колебаний.

В СИ [T] = 1 с ; [w_o ] = 1 рад/c = 1 c^-1

Частотой колебаний называется число полных колебаний, совершаемых в единицу времени:

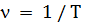
(6)

В СИ [ n ] = 1 Гц = 1 с^-1

Введем понятия линейной и круговой ( циклической ) частот колебания.

Величина, обратная периоду колебаний, называется линейной частотой колебаний.

1 Гц - частота периодического процесса, при которой за 1 с совершается один цикл процесса.

    Сравнивая (4) и (6) получае ,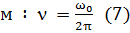 

wo = 2 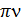 , ( 8) где   wo – круговая ( циклическая ) частота колебаний.

Вывод расчетной формулы

 

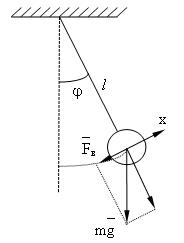Математическим маятником называется идеализированная система, состоящая из материальной точки, массы m, подвешенной на нерастяжимой невесомой нити и совершающей колебания под действием силы тяжести.

 

Рис. 1. Математический маятник

Выведем формулу для расчета величины полной механической энергии математического маятника.

Полная механическая энергия маятника складывается из суммы кинетической и потенциальной энергий:

По определению: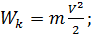

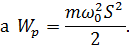
(10) (11)

Для нахождения величины полной механической энергии необходимо найти   скорость, с которой совершает колебания математический маятник. Величиной совершающей гармонические колебания является величина S – смещение маятника от положения равновесия. 

Пусть гармонические колебания маятника совершаются по закону косинуса.

Тогда уравнение гармонических колебаний математического маятника имеет вид:
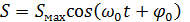                              (12)

Из определения скорости получаем:

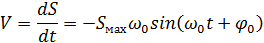
(13)

 Теперь запишем выражение для кинетической энергии гармонических колебаний математического  маятника:

:

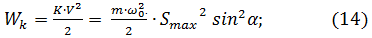
 По определению величина потенциальной энергии гармонических колебаний маятника равна :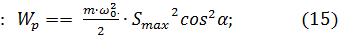

Запишем выражения полной энергии материальной точки.

+

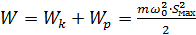(16)

  Так как  m = const, w_о = const, S_max = const, то из соотношения (16) следует вывод:

Порядок выполнения работы

1. Отклонить маятник на угол α < 10° и определить время 10  полных колебаний. Вычислить период колебаний по формуле :  Т₀ = t/10, результаты вычислений занести в таблицу 1.

2. Определить величину амплитуду колебаний по формуле: S _max = l sina

3.  Рассчитать величину циклической частоты колебаний маятника и квадрат ее  величины по формуле: w_o = 2p/Т, результаты  вычислений занести в таблицу 1.

4. Рассчитать величину полной механической энергии гармонических колебаний по формуле : 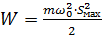,  результаты вычислений занести в таблицу 1.

5. Изменяя длину маятника, повторить измерения, указания в п. 1 для 4 различных значений длины l,  расчеты соответствующих величин внести в таблицу 1.

                                                                                                         Таблица 1.

	l ,(м)	t, (с)	Т0, (с)	ω0, (с)	S max (м)	Wполн (Дж)
1
2
3
4
5

 

6. Рассчитать погрешность ∆Т (принять погрешность расчета периода колебаний математического маятника равной погрешности измерения секундомера):

7. Записать окончательный результат в стандартном виде:

Т =  < Т> ± ∆ Т

8. Рассчитать величинуW. Сделать выводы по результатам выполненной работы.

9. Оформить бланк отчета.

7. Контрольные вопросы

1. Какой маятник называется математическим?

2. Как в данной лабораторной работе определяется период колебаний математического маятника?

3. Каким способом рассчитывается погрешность измерений периода колебаний математического маятника в данной работе?

4. Какие движения или процессы называются колебаниями?

5. Какие колебания называются гармоническими?

6. Какая величина называется амплитудой колебания?

7. Какая величина называется периодом колебаний?

8. Какая величина называется циклической частотой?

9. Какая величина называется линейной частотой?

10. Запишите формулу, определяющую:

· период колебаний математического маятника;

· циклическую частоту колебаний математического маятника;

· величину линейной скорости колебаний математического маятника;

· величину  кинетической энергии механических гармонических колебаний математического маятника;

· величину  потенциальной энергии механических гармонических колебаний математического маятника;

· величину максимального смещения маятника от положения равновесия;

· величину полной механической энергии гармонических колебаний математического маятника.

Задачи

1. Уравнение движения точки дано в виде x=2 sin ( ( p / 2 ) × t + p / 4 ) см.

Найти период колебаний. Ответ: 4 сек. 

2. Уравнение движения точки дано в виде x=2 sin ( ( p / 2 ) × t + p / 4 ) см.

Найти: максимальную скорость точки. Ответ: 3,14×10-2 м/сек. 

3. Уравнение движения точки дано в виде x=2 sin ( ( p / 2 ) × t + p / 4 ) см.  Найти ее максимальное ускорение. Ответ: 4,93×10^-2 м/сек².  

4. Точка совершает гармоническое колебание. Период колебаний 2 сек, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда смещение точки от положения равновесия равно 25 мм. Ответ: 0,136 м/сек.

5. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 2,4 см, скорость точки равна 3 см/сек, а при смещении, равном 2,8 см, скорость равна 2 см/сек. Найти амплитуду этого колебания. Ответ: А=3,1×10^-2 м.

6. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 2,4 см, скорость точки равна 3 см/сек, а при смещении, равном 2,8 см, скорость равна 2 см/сек. Найти период этого колебания. Ответ: Т=4,1 сек.

7. Определить начальную фазу гармонических колебаний тела, если через 0,25 с после начала движения смещение его было равным половине амплитуды. Период колебаний 6 с. Ответ: π / 12.

8. Считая движение поршня в цилиндре автомобильного двигателя гармоническими колебаниями, определить максимальное значения модуля его скорости, если автомобиль движется с модулем скорости 72 км/ч на прямой передаче, радиус колес 334 мм, ход поршня 100 мм. Ответ:29 м/с.

 Бланк отчета

Тольяттинский государственный университет

Отчет

По лабораторной работе №5

«Определение величины полной механической энергии гармонических колебаний математического маятника»

К работе допущен

Работа выполнена

Работа зачтена

Тольятти 2019

Цель работы − Изучить законы гармонических колебаний, экспериментально получить значение периода, циклической частоты и полной механической энергии гармонических механических колебаний математического маятника.

Приборы и принадлежности

Экспериментальная установка, состоящая из штатива со шкалой, и шарика, подвешенного на невесомой, нерастяжимой нити.

 

 Схема (экспериментальной установки) с указанием ее основных частей.

 

 

Расчетные формулы:

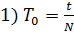, где N- число полных колебаний маятника;

2) S _max = l sina , где l - длина маятника, a - угол отклонения нити маятника от вертикали;

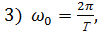 где величину принять равной π = 3,14;

 

4)

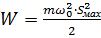
Исходные данные: l ₁ = 1,00 м; l ₁ = 0,70 м; l ₁ = 0,60 м; l ₁ = 0,50 . ;

Результаты измерений и вычислений:

                                                                                                         Таблица 1.

	l ,(м)	t, (с)	Т0, (с)	ω0, (с)	S max (м)	Wполн (Дж)
1
2
3
4
5

 

10. Рассчитать погрешность ∆Т (принять погрешность расчета периода колебаний математического маятника равной погрешности измерения секундомера):

11. Записать окончательный результат в стандартном виде:

Т =  < Т> ± ∆ Т

12. Рассчитать величину полной механической энергии W. Сделать выводы по результатам выполненной работы.

13. Оформить бланк отчета.

 

 

Институт математики, физики и информационных технологий