Пусть дана Z - задача оптимизации –пара ( F, c) , где F –множество решений, а – c функция стоимости, отображающая элементы F на множество действительных чисел. Требуется найти такую x* точку из F, на которой значение функции c(x*) обладает определенным свойством, например, минимально, максимально и пр. Рассмотрим, например, задачу на минимум.
В задаче коммивояжера – это множество всех гамильтоновых циклов графа, в задаче ЦЛП – множество целочисленных точек многогранника и т.п.
Методы направленного перебора основаны на нескольких простых соображениях.
1. Экстремальное значение на множестве и на подмножестве связаны определенными неравенствами. В случае задачи на минимум cG - минимум функции стоимости на подмножестве G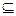 
F не превосходит c(x*) - минимума функции стоимости на всем множестве.
2. Пусть l(x*)≤ c(x*) ≤ u(x*), т.е. l(x*) и u(x*) - нижняя и верхняя оценка для c(x*). При этом значения l(x*) и u(x*) могут быть найдены полиномиальным алгоритмом.
3. Все множество F может быть иерархически разбито на непересекающиеся подмножества. Это разбиение представимо в виде дерева ветвей. Пример приведен на рисунке.
Здесь каждая вершина – некоторое множество допустимых решений. Все множество решений, соответствующее каждому родительскому узлу разбивается на подмножества решений, соответствующих узлам-потомкам. Здесь все подмножества родительского узла не пересекаются, а их объединение в точности дает множество, соответствующее родительскому узлу. Листья дерева – одноэлементные множества.
4. Если для некоторого узла дерева G 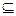F выполняется соотношение
l(x*)<cG,
то это означает, что оптимальное решение x* не может находиться среди опустимых решений, соответствующих данному узлу, а все множество G можно исключить из дальнейшего рассмотрения. (Отрезать ветвь дерева.)
Отсюда следует другое название методов направленного перебора – методы ветвей и границ.
Коммуникационная сложность
Этот подход к оценке сложности задач в некотором смысле связан с предыдущим и, так же как и параллельные вычисления, обусловлен, в первую очередь, развитием компьютерной техники.
В случае параллельных вычислений основная забота – эффективно использовать вычислительный ресурс. В модели параллельных вычислений процессоры обмениваются информацией. Время обмена информацией и стоимость такого обмена полагается пренебрежительно малой по сравнению со временем и стоимостью вычислений.
Если же поменять акценты на противоположные: время и стоимость вычислений пренебрежительно мала по сравнению временем обмена информацией и стоимостью такого обмена – получаем подход, называемый коммуникационной сложностью. Обсчет сложных физических экспериментов научными центрами, обмен информацией между гидрометцентрами в реальном времени для составления прогноза погоды и т.п. – это реальные современные задачи, которые встают в условиях распределенных хранилищ информации, критичности времени обмена и не всегда разумной стоимостью трафика как коммуникационного ресурса.
Так же, как и в случае параллельных вычислений, модель коммуникационного взаимодействия между хранилищами информации в процессе совместного решения конкретной индивидуальной задачи – это предмет постановки задачи. Такая модель обычно связывается с понятием коммуникационного протокола. Три основных группы параметров модели связаны со следующими ее составляющими.
1. Участники. Это процессоры (ФУ, серверы, ЛВС предприятий и т.п.), осуществляющие вычисления (обработку информации) на местах (в точках распределенной сети). Они могут быть равноправны и неравноправны, потребность в информации (обращении) каждого участника со стороны остальных может быть разной и т.д.
2. Линии связи. Стоимость обмена данными может зависеть от конкретной пары обменивающихся участников. Она может быть несимметричной. Пропускная способность канала связи может быть ограниченной и пр.
3. Ограничения на возможности (правила) обмена информацией. Не все участники могут одновременно получать и отправлять информацию (кто-то может делать только одно из этих действий). Друг с другом можно связать только определенные пары участников. И т.д.
Все эти параметры в модели вычислений должны быть оговорены и тогда они станут частью протокола вычислений, который на их основе опишет правила работы получившейся распределенной вычислительной системы. Те, кто работал с СУБД, сразу смогут увидеть здесь аналогию этого протокола с протоколами обработки распределенной базы данных.
В теории сложности в качестве базового случая рассматривается простейший: два равноправных участника (Алиса и Боб) с симметрично распределенной между ними входной информацией совместно вычисляют булеву функцию f(x1,…,xn), обмениваясь в процессе вычисления сообщениями фиксированной длины (они называются битами). Процесс обмена представляется корневым ориентированным деревом (корень ассоциируется с инициатором обмена), каждая промежуточная вершина которого соответствует участнику посылающему информацию, висячая вершина – результату вычислений, а ребро значению бита (0 или 1). Такое дерево называется протоколом вычисления функции f, а длиной протокола называется максимум длины пути в этом дереве. Вообще говоря, даже в нашем простейшем случае можно построить разные протоколы (как можно построить разные машины Тьюринга для решения одной и той же задачи), поэтому формально определение коммуникационной сложности для рассматриваемой модели вычислений выглядит следующим образом.
Опр. Коммуникационная сложность вычисления функции – это минимум по длинам всех протоколов, вычисляющих эту функцию.
Получаем такой min- max –ый критерий. До сих пор мы имели дело с max- min-ми критериями: определение сложности «в худшем», функция Шеннона и пр.
Ниже приведен пример совместной проверки участниками равенства x1y2=x1y2.
Очевидно, что в нашей простейшей модели коммуникационная сложность любой задачи не превосходит O(n) (здесь n, как обычно, обозначает длину входа задачи). Действительно, тривиальный протокол, состоящей в единичной посылке своих данных одним участником другому приводит к вычислению функции. (Еще раз подчеркнем, что в нашей модели трудоемкость самих вычислений равна нулю).
Приведем несколько примеров задач. Коммуникационная сложность которых может быть меньше O(n).
Пример. Задача «четность». Дано два булевых вектора: x (находится у Алисы) и y (находится у Боба). Определить четность длины вектора конкатенации xy.
Задача решается за О(1) путем посылки четности своей части одним участником другому.
Пример. Задача «сумма бит». Дано два булевых вектора одинаковой длины n: x (находится у Алисы) и y (находится у Боба). Определить, одинаково ли число единиц в этих векторах.
Задача решается за О(logn) очевидным образом путем посылки суммы единиц своей части одним участником другому.
Пример. Задача «эквивалентность». Дано два булевых вектора одинаковой длины n: x (находится у Алисы) и y (находится у Боба). Определить эквивалентны ли они.
Задача решается за О(n) тривиальным алгоритмом путем посылки своего вектора одним участником другому. Оказывается, что ее нельзя решить быстрее. Это, в каком-то смысле тривиальное следствие теоремы Шеннона из теории информации. Вектора битовые. Каждый участник должен получить информацию о каждом бите, но нельзя бит закодировать информацией меньшей длины, чем один бит.
Но это тривиальные примеры. Учебник по коммуникационной сложности начинается, обычно, со следующего, менее очевидного примера.
Пример. Задача «медиана». Медианой упорядоченного числового множества из n элементов называется элемент этого множества, стоящая на ]n/2[ месте. Алиса и Боб имеют по одному подмножеству множества {1,2,…,n}. Требуется найти медиану объединения подмножеств Алисы и Боба.
Легко построить алгоритм решения со сложностью O(log2n). Для этого заметим, что медиана всего множества лежит между медианами частей Алисы и Боба. Вначале Боб посылает Алисе свою медиану, Алиса в ответ посылает ему медиану той части своего множества, которая лежит между ее медианой и медианой Боба и т.д. Получаем сходящуюся дихотомию, в которой не больше O(logn) шагов и на каждом шаге посылается O(logn) битов.
Однако можно построить и более экономный алгоритм сложности O(logn).
Рассматриваются и более общие (по сравнению с моделью Алиса-Боб) модели. Они, как правило, имеют практическое обоснование и учет их специфики приводит либо к тривиальным результатам, либо требует решения технически сложных задач на стыке комбинаторной математики и теории телекоммуникационных протоколов. Важно, что вы должны знать о существовании таких постановок и при столкновении с ними в своей будущей инженерной деятельности сможете, при желании, найти результаты тридцатилетних исследований в этой области. А, если эти результаты вам не помогут, то можете переквалифицироваться в математиков и попытаться внести свой вклад в эти исследования.
Заключение
Предложенный здесь текст обладает рядом свойств.
1. Он является базовым как для объема 17 лекций – 17 семинаров (для студентов по программе «специалист», так и для объема 17 лекции – 9 семинаров (для магистратуры).
2. Сам материал является классическим и в той или иной мере присутствует в аналогичных курсах ведущих Вузов России. Однако, подбор материала, логика изложения и акценты ориентированы на специфику подготовки студентов кафедры ИУ-8.
3. Для студентов, желающих углубить и расширить свои знания в этой области, автор постарался привести (в минимальном объеме) необходимые источники, освоение которых должно быть не очень затруднительным при условии овладения предлагаемым здесь текстом лекций.
4. Предполагается, исходя из методического плана подготовки на кафедре ИУ-8, что студент, освоивший предмет в полной мере, готов к пониманию курсов «Алгоритмы и структуры данных» и «Исследование операций».
5. Во многом тематика данного курса явилась поводом для изложения в нем подготовительных материалов для другой дисциплины- курса по выбору: «Дополнительные главы теории сложности алгоритмов».
13. Задачи и вопросы для самопроверки по курсу «Математическая логика и теория алгоритмов».
Задачи.
Задача 1.1 Написать на любом языке алгоритм находящий минимальное из n чисел и оценить его трудоемкость.
Задача 1.2 Написать на любом языке алгоритм сортирующий n чисел и оценить его трудоемкость.
Задача 1.3 Для заданного графа с 8 вершинами построить примеры: цикла, контура, гамильтонова цикла, клики, вершинного покрытия.
Задача 1.4 Написать на любом языке алгоритм распознавания простоты натурального n и оценить его трудоемкость.
Задача 1.5 Для 6 камней с заданными весами написать алгоритм решения задачи о камнях и оценить его трудоемкость.
Задача 2.1 Построить НАМ f(x)= 3.
Задача 2.2 Построить НАМ f(x,y)=x+êx-yú.
Задача 2.3 Построить НАМ f(x,y,z)=z+êx-yú.
Задача 2.4 Построить НАМ, преобразующую слово P в слово PP.
Задача 3.1 . Построить МТ, вычисляющую функцию f(x,y,z)=z.
Задача 3.2. Построить МТ, вычисляющую функцию f(x)=x+1.
Задача 3.3. Построить МТ, вычисляющую функцию f(x,y)=x+y.
Задача 3.4. Построить МТ, вычисляющую функцию f(x,y,z)=z+êx-yú.
Задача 4.1. Построить МТ, записывающую буквы любого слова некоторого конечного алфавита в обратном порядке.
Задача 4.2. Построить МТ, преобразующую слово P в слово PP.
Задача 4.3. Для входного алфавита {b, c} построить МТ, "различающую" слова, содержащие b от остальных.
Задача 4.4 Определена машина Тьюринга (см. лекции) T = {S, A, F, q0, d}, d - упорядоченная последовательность команд. Доказать, что определение МТ эквивалентно определению, в котором команды перехода - L, R, St – включены в алфавит. (Докажите это в виде простого упражнения.).
Задача 5.1 Для функции f построить схему в базисе B.
· f= xÚy, B={Ù,»}.
· F=xÅyz, B={®,ù}.
Задача 5.2. Для системы функций построить схему в базисе B.
· F=xyÚxzÚzy, g=xÅzÅy; B={Å,Ù}.
· F=ùx, g=ùxùy, h=1, T=ùxùzùy; B={ù,¯}.
Задача 5.2. Для функции f построить схему сложности не выше m в базисе B={Ù,Ú,ù}.
· f=x»y, m=4.
· F=ùxùy, m=2.
Задача 6.1. Доказать, что задача "гамильтонов цикл" сводится к задаче "коммивояжер".
Задача 6.2 Доказать, что задача "КНФ выполнимость" сводится к задаче "клика".
Задача 6.3 Доказать, что задача «3-выполнимости" сводится к задаче "ЦЛП".
Задача "ЦЛП" (целочисленного линейного программирования) :
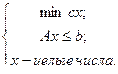
Задача 7.1. Доказать полиномиальную разрешимость задачи «2-КНФ».
Задача 7.2. Доказать NP- полноту задачи «вершинное покрытие». ( Вершины вершинного покрытия содержатся во всех ребрах графа).
Задача 8.1 Для задач из класса NP, рассмотренных на предыдущих трех занятиях, сформулировать соответствующие задачи из класса co-NP.
Задача 8.2 Для алгоритмов, рассмотренных на Занятии 1 оценить используемую память.
Задача 8.3 Для задачи «k-е по порядку подмножество» оценить используемую память.
Вопросы.
· Понятие «задача». Форма задачи. Индивидуальная и массовая задача. Привести примеры.
· Определение Машины Тьюринга (МТ). Различие детерминированной и недетерминированной МТ.
· Определение Оракульной Машины Тьюринга (ОМТ). Различие оракульной и недетерминированной МТ.
· Определение Недерминированной Машины Тьюринга (НМТ). Привести пример.
· Задание «входа» для индивидуальной задачи. Примеры кодировок графов. Понятие полиномиальной эквивалентности для различных кодировок объекта.
· Классы P, NP, NPC. Соотношение между ними.
· Привести примеры выполнимой и общезначимой формулы в исчислении предикатов.
· Классы PSPASE, NPSPASE. Соотношение между ними.
· Классы PSPASE, EXPTIME. Соотношение между ними.
· Определение СФЭ. Пример СФЭ.
· Классы P/Poly и P. Соотношение между ними.
· Построить НАМ для обращения слов в заданном алфавите.
· Класс PSPASE и игра двух лиц. Соотношение между ними.
· По заданной формуле в исчислении предикатов построить формулу в приведенной нормальной форме.
· Отношения. Сводимость по Тьюрингу.
· Примеры полиномиально разрешимых частных случаев NP –полных задач.
· Предикат. Формула в исчислении предикатов. Выполнимые и общезначимые формулы. Приведенная нормальная форма.
· Теорема Кука. Схема доказательства.
· Понятие алгоритма. Эквивалентность алгоритмов. Тезис Черча.
· Алгоритм нахождения кратчайшего пути между вершинами графа.
· Примеры подходов к решению NP-полных задач.
· Определение полиномиальной сводимости и сводимости по Тьюрингу. Пример полиномиальной сводимости.
· Теорема о PSPACE-полной задаче.
· Классы NP и co-NP. Соотношение между ними. Теорема об NP–полной задаче и классе Co-NP.
· Приближенные алгоритмы с оценкой точности. Теорема о существовании такого алгоритма для «Задачи коммивояжера».
· Игра двух лиц. Определение. Игра двух лиц и классы NP и co-NP.
· Коммуникационная сложность. Коммуникационная сложность задачи о равенстве числа единиц в двух булевских векторах.
· По заданной формуле в исчислении предикатов построить формулу в приведенной нормальной форме.
14. Рекомендованная литература
1. Ахо А.А., Хопкрофт Д.Э., Ульман Д.Д. Структуры данных и алгоритмы. М.: Вильямс, 2007. – 400 с.
2. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 2012.
3. Мендельсон Э. Введение в математическую логику. М.: Наука, 2012.
4. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. М.: Мир, 1984.
5. Гордеев Э.Н. Задачи выбора и их решение. – Сб. «Компьютер и задачи выбора. М.: Наука, 1989.
6. Кузюрин Н.Н., Фомин С.А. Эффективные алгоритмы и сложность вычислений.М: МФТИ, 2007.
7. Лупанов О.Б. Курс лекций по дискретной математике. - Конспект лекций. МГУ. 2012.
Дата: 2019-07-30, просмотров: 252.
