Логика предикатов представляет собой развитие логики высказываний. Она содержит в себе логику высказываний, т.е. элементарные высказывания, рассматриваемые как величины, которые принимают значения И либо Л. Но помимо этого, язык логики предикатов вводит в рассмотрение утверждения, содержащие высказывания типа «для любого» и «существует», которые обозначаются кванторами всеобщности и существования.
Опр. n-местный предикат – это отношение на декартовом произведении n множеств.
Содержательно эти n множеств могут быть различными. Но, если взять их объединение, то можно получить некоторое множество M. Тогда n-местный предикат – это отношение на декартовом произведении n множеств М.
Одноместный предикат – это свойство.
Например, если N – множество натуральных чисел, то одноместный предикат четность P(x) принимает значение И (или 1), если x –четное, а двухместный предикат больше P(x,y) принимает значение И (или 1), если x>y.
Если же не будем фиксировать элемент множества М, например, рассмотрим P(х), где х - любой элемент M, то получим некоторое предложение, которое становится высказыванием, когда х замещено определенным элементом M. Например, если M является множеством всех натуральных чисел, а А(х) предикат простота числа, то предложение становится высказыванием, если х заменить числом, например, "3 -простое число", "4-простое число". При этом получаем высказывания, которые истинны, либо ложны. Следовательно, А(х) порождает отношение на множестве М.
Вводятся специальные обозначения. Пусть M -множество, Р(х) - определенный на M одноместный предикат. Тогда выражение  хР(х) означает: "для всех х Р(х)" или "для всех х выполняется Р(х)", или "для любого х Р(х)", или "для каждого х Р(х)". Под выражением
хР(х) означает: "для всех х Р(х)" или "для всех х выполняется Р(х)", или "для любого х Р(х)", или "для каждого х Р(х)". Под выражением  хР(х) подразумевается высказывание истинное, когда Р(х) истинно для каждого х из M и ложное - в противном случае. Символ
хР(х) подразумевается высказывание истинное, когда Р(х) истинно для каждого х из M и ложное - в противном случае. Символ  называется квантором всеобщности. Выражение
называется квантором всеобщности. Выражение 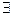 хР(х) означает "существует х такое, что Р(х)" или "хотя бы для одного х Р(х)", или "для некоторого х Р(х)". Под выражением
хР(х) означает "существует х такое, что Р(х)" или "хотя бы для одного х Р(х)", или "для некоторого х Р(х)". Под выражением 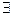 хР(х) подразумевается высказывание, которое истинно, если Р(х) принимает значение И хотя бы для одного значения переменной х из M, и ложно, если Р(х) для всех значений переменной х принимает значение Л. Символ
хР(х) подразумевается высказывание, которое истинно, если Р(х) принимает значение И хотя бы для одного значения переменной х из M, и ложно, если Р(х) для всех значений переменной х принимает значение Л. Символ 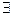 называется квантором существования.
называется квантором существования.
Пусть Р(х1,х2,...,хп) -n-местный (п>2) предикат. Выражение  х iР(х1,х2,...,хп), 1 < i < n, является (n-1)-местным предикатом, зависящим от (свободных) переменных х1,х2,...,х i-1,х i+1,...,х n, причем высказывание
х iР(х1,х2,...,хп), 1 < i < n, является (n-1)-местным предикатом, зависящим от (свободных) переменных х1,х2,...,х i-1,х i+1,...,х n, причем высказывание  хiР(а1,а2,...,а i-1, хi,а i+1,...,а n) истинно тогда и только тогда, когда для любого значения а истинно высказывание Р(а1,а2,...,а i-1, a,а i+1,...,а n). Выражение
хiР(а1,а2,...,а i-1, хi,а i+1,...,а n) истинно тогда и только тогда, когда для любого значения а истинно высказывание Р(а1,а2,...,а i-1, a,а i+1,...,а n). Выражение 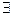 х iР(х1,х2,...,хп), 1 < i < n, является (n-1)-местным предикатом, зависящим от (свободных) переменных х1,х2,...,х i-1,х i+1,...,х n, причем высказывание
х iР(х1,х2,...,хп), 1 < i < n, является (n-1)-местным предикатом, зависящим от (свободных) переменных х1,х2,...,х i-1,х i+1,...,х n, причем высказывание 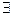 хiР(а1,а2,...,а i-1, хi,а i+1,...,а n) истинно тогда и только тогда, когда для хотя бы одного значения а истинно высказывание Р(а1,а2,...,а i-1, a,а i+1,...,а n).
хiР(а1,а2,...,а i-1, хi,а i+1,...,а n) истинно тогда и только тогда, когда для хотя бы одного значения а истинно высказывание Р(а1,а2,...,а i-1, a,а i+1,...,а n).
Квантор всеобщности является обобщением (аналогом) конъюнкции, а квантор существования - обобщением (аналогом) дизъюнкции на произвольное, не обязательно конечное, множество значений переменной. На самом деле, можно было бы обойтись одним квантором, так как они выражаются друг через друга, например, выражение  хА( x) эквивалентно выражению.
хА( x) эквивалентно выражению. 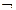 (
( 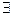 х(
х( 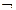 А( x))).
А( x))).
Навешивание квантора по переменной х связывает переменную х. Понятие «связанная переменная» аналогично понятиям: индекс суммирования в комбинаторике, переменная интегрирования в матанализе или параметр цикла в программе. Вне суммы, интеграла или цикла не имеет значения, какой буквой они обозначены. При этом, если такая же буква встречается вне суммы, интеграла или цикла, то это другая буква с тем же обозначением. Например, в формуле
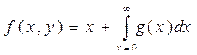
переменная x под интегралом и переменная x вне интеграла – это разные переменные.
Поэтому во избежание недоразумений одну из этих переменных переобозначают. Для определенности, положим, что это связанная переменная. Такое переобозначение называется правилом переименования связанных переменных.
Понятие формулы в исчислении предикатов требует некоторых предварительных замечаний. Буквы начала латинского алфавита (а, b,с,...) и они же с числовыми индексами (а1,а2,..., b1, b2,...,с1,с2,...) называются предметными константами. Буквы конца латинского алфавита (х,у,...) и они же с числовыми индексами (х1,х2,...,у1,у2,..., z1, z2,... ) называются предметными переменными. Буквы An с числовыми индексами i > 1, п > 0, называются предикатными буквами, а fin, i > 1, п > 1, - функциональными буквами. Верхний индекс предикатной или функциональной буквы указывает число аргументов, а нижний индекс служит для различения букв с одним и тем же числом аргументов.
Числовые индексы у предикатных и функциональных букв часто опускаются, если они понятны из контекста. Например, вместо  (х,у) пишут А1(х,у), и если нет других двухместных предикатных букв А Вместо А1(х,у) пишут А(х,у), если другие предикаты обозначаются другими буквами.
(х,у) пишут А1(х,у), и если нет других двухместных предикатных букв А Вместо А1(х,у) пишут А(х,у), если другие предикаты обозначаются другими буквами.
Определение терма:
а) всякая предметная переменная или предметная постоянная есть терм;
б) если fin - функциональная буква и t1, t2,..., tn - термы, то fin ( t1, t2,..., tn) есть терм;
в) выражение является термом только в том случае, если это следует из правил а) и б).
Примеры термов: а, х1, f (х,а), G (а, f (у)).
Предикатные буквы, примененные к термам, порождают элементарные формулы, или точнее: если Ain - предикатная буква, а t1, t2,..., tn - термы, то  - элементарная формула. При этом считается, что нульместная предикатная буква тоже является элементарной формулой.
- элементарная формула. При этом считается, что нульместная предикатная буква тоже является элементарной формулой.
Примеры элементарных формул: A1, A1 (х1,а1), А1( f(х)), А3( a, x, f(х, y, b)).
Определение формулы требует фиксации некоторого базиса (полной системы логических связок). Традиционный пример выглядит следующим образом.
Опр. Формулы логики предикатов определяются следующим образом:
а) всякая элементарная формула есть формула;
б) если А и В - формулы и х - предметная переменная, то каждое из
выражений ( 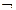 А), (А→В), (
А), (А→В), (  хА) есть формула;
хА) есть формула;
в) выражение является формулой только в том случае, если это
следует из правил а) и б).
Отдавая дань традиционным обозначениям и определения, мы использовали полную систему логических связок ( 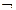 ,→) -отрицание, импликация. Но вместо этого можно использовать любую другую полную систему логических связок (функций). (Вспомните теорему Поста.) Поэтому в формулах исчисления предикатов используются любые логические связки, потому что подразумевается, что их всегда можно выразить через полную систему функций (
,→) -отрицание, импликация. Но вместо этого можно использовать любую другую полную систему логических связок (функций). (Вспомните теорему Поста.) Поэтому в формулах исчисления предикатов используются любые логические связки, потому что подразумевается, что их всегда можно выразить через полную систему функций ( 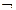 ,→).
,→).
Опр. Длина l(F) формулы F – это количество входящих в ее запись букв и логических связок.
Для сокращения количества скобок действует обычное старшинство связок, а кванторы, например, идут по старшинству после связок: отрицание, конъюнкция, дизъюнкция, но перед импликацией и эквивалентностью.
В выражениях (  хА) и (
хА) и ( 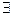 хА) формула А называется областью действия кванторов
хА) формула А называется областью действия кванторов  х и
х и 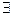 х соответственно.
х соответственно.
Договоримся также опускать скобки, в которые заключается формула А в формулах вида ( Q1( Q2(…))), где Q1 и Q2 … -любые кванторы. Например, вместо
(  х(
х(  у(
у( 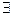 z(A1 (х,у, z))))) пишут
z(A1 (х,у, z))))) пишут  х
х  у
у 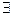 zA1 (х,у, z).
zA1 (х,у, z).
Вхождение переменной х в данную формулу называется связанным, если х является переменной входящих в эту формулу кванторов  х,
х, 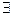 х или находится в области действия входящих в эту формулу кванторов
х или находится в области действия входящих в эту формулу кванторов  х,
х, 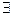 х; в противном случае вхождение переменной х в данную формулу называется свободным. Например, вхождение переменной х в формулу
х; в противном случае вхождение переменной х в данную формулу называется свободным. Например, вхождение переменной х в формулу  у A1 (х,у)=A2 (у,у) является свободным, первое и второе вхождение переменной у - связанное, а третье и четвертое вхождение у в эту формулу -свободное. Таким образом, одна и та же переменная в одной и той же формуле может иметь как связанные, так и свободные вхождения. (Это просто означает, что одной буквой обозначены разные сущности.) Переменная называется свободной (связанной) переменной в данной формуле, если существуют свободные (связанные) ее вхождения в эту формулу.
у A1 (х,у)=A2 (у,у) является свободным, первое и второе вхождение переменной у - связанное, а третье и четвертое вхождение у в эту формулу -свободное. Таким образом, одна и та же переменная в одной и той же формуле может иметь как связанные, так и свободные вхождения. (Это просто означает, что одной буквой обозначены разные сущности.) Переменная называется свободной (связанной) переменной в данной формуле, если существуют свободные (связанные) ее вхождения в эту формулу.
Формула называется замкнутой, если она не содержит никаких свободных переменных, т.е. либо все ее переменные связанные, либо переменных нет совсем. Нам в дальнейшем потребуется понятие выполнимых и общезначимых формул исчисления предикатов. А эти понятия определяются через понятие интерпретации.
Интерпретацию будем считать заданной, если:
1. Задано непустое множество М, называемое областью интерпретации.
2. Заданы следующие соответствия:
· предикатным буквам An поставлены в соответствие некоторые n -местные предикаты (отношения) в М;
· функциональным буквам fin поставлены в соответствие некоторые n -аргументные функции, отображающие М n в М;
· каждой предметной постоянной поставлен в соответствие некоторый (фиксированный) элемент из М;
· кванторам и логическим связкам поставлен в соответствие их обычный смысл.
Например, чтобы задать интерпретацию для формулы  xA(x,y, b1), нужно задать множество М - область интерпретации (область изменения переменных x,y). Из этой области М будем брать некоторый элемент, соответствующий предметной постоянной b1. Далее нужно задать 3-х местный предикат на М, соответствующей предикатной букве A. Так, можно положить, что М – множество натуральных чисел, предметной постоянной b1 поставить в соответствие 3, а A ( x, y, z) поставить в соответствие предикат x + y > z. Тогда формула
xA(x,y, b1), нужно задать множество М - область интерпретации (область изменения переменных x,y). Из этой области М будем брать некоторый элемент, соответствующий предметной постоянной b1. Далее нужно задать 3-х местный предикат на М, соответствующей предикатной букве A. Так, можно положить, что М – множество натуральных чисел, предметной постоянной b1 поставить в соответствие 3, а A ( x, y, z) поставить в соответствие предикат x + y > z. Тогда формула  xA(x,y, b1) в заданной интерпретации запишется:
xA(x,y, b1) в заданной интерпретации запишется:  x(x + y >3)- и означает, что для любого натурального x сумма x + у больше 3. Очевидно, что это отношение истинно при некоторых у (у > 2) и ложно при других значениях у (0<у<3). Если предметной постоянной b1 поставить в соответствие 0, а не 3, то утверждение
x(x + y >3)- и означает, что для любого натурального x сумма x + у больше 3. Очевидно, что это отношение истинно при некоторых у (у > 2) и ложно при других значениях у (0<у<3). Если предметной постоянной b1 поставить в соответствие 0, а не 3, то утверждение  x(x + y > 0) будет истинно при любом значении свободной переменной у.
x(x + y > 0) будет истинно при любом значении свободной переменной у.
Легко видеть, что для той же формулы  xA(x,y, b1) можно построить бесчисленное множество других интерпретаций, выбирая различные множества М, выбирая из М каким-то образом элемент, соответствующий b1, и задавая различным образом на М трехместный предикат.
xA(x,y, b1) можно построить бесчисленное множество других интерпретаций, выбирая различные множества М, выбирая из М каким-то образом элемент, соответствующий b1, и задавая различным образом на М трехместный предикат.
При данной интерпретации всякая формула без свободных переменных (замкнутая формула) представляет собой высказывание, которое истинно либо ложно, а всякая формула со свободными переменными выражает некоторое отношение на М, которое может быть истинно для одних значений из М и ложно для других.
Опр. Формула называется выполнимой в данной интерпретации, если она принимает значение И хотя бы для одной совокупности возможных значений её свободных переменных (если они есть). Если формула не содержит свободных переменных, то она называется выполнимой в том случае, если принимает значение И в этой интерпретации.
Опр. Формула называется истинной в данной интерпретации, если она принимает значение И для всех возможных значений её свободных переменных (если они есть). Если же свободных переменных нет, то формула называется истинной, когда она принимает значение И в этой интерпретации.
Опр. Формула называется ложной в данной интерпретации, если она принимает значение Л для всех возможных значений её свободных переменных (если они есть). Если же свободных переменных нет, то формула называется ложной, когда она принимает значение Л в этой интерпретации. Очевидно, что формула ложна в данной интерпретации тогда и только тогда, когда она не выполнима в этой интерпретации. Так же ясно, что формула A выполнима в данной интерпретации тогда и только тогда, когда она не является ложной в этой интерпретации.
Данная интерпретация называется моделью для множества формул G, если каждая формула из G истинна в этой интерпретации.
Можно доказать следующие свойства формул в данной интерпретации.
· Формула 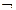 A ложна в данной интерпретации тогда и только тогда, когда A истинна в этой же интерпретации. Формула A истинна в данной интерпретации тогда и только тогда, когда
A ложна в данной интерпретации тогда и только тогда, когда A истинна в этой же интерпретации. Формула A истинна в данной интерпретации тогда и только тогда, когда 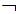 A ложна в этой же интерпретации.
A ложна в этой же интерпретации.
· Никакая формула не может быть одновременно истинной и ложной в одной и той же интерпретации.
· Если в данной интерпретации истинны A и A→ B, то истинно и B.
· Формула A→ B ложна в данной интерпретации тогда и только тогда, когда A истинно в этой интерпретации, а B ложно.
· Формула A& B выполнима в данной интерпретации тогда и только тогда, когда A и B принимают значение И одновременно хотя бы для одной совокупности значений своих свободных переменных. Если же свободных переменных нет, то формула A& B выполнима в данной интерпретации тогда и только тогда, когда обе формулы A и B истинны в этой интерпретации.
· Формула A  B выполнима в данной интерпретации, если хотя бы одна из них выполнима в этой интерпретации.
B выполнима в данной интерпретации, если хотя бы одна из них выполнима в этой интерпретации.
· Формула A= B выполнима в данной интерпретации тогда и только тогда, когда A и B принимают значение И одновременно или значение Л (тоже одновременно) хотя бы для одной совокупности значений своих свободных переменных. Если же свободных переменных нет, то формула A= B выполнима в данной интерпретации тогда и только тогда, когда A и B принимают одинаковые истинностные значения в этой интерпретации.
· Формула 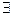 хА выполнима в данной интерпретации тогда и только тогда, когда A принимает значение И хотя бы для одной совокупности значений её свободных переменных и хотя бы одного значения переменной x.
хА выполнима в данной интерпретации тогда и только тогда, когда A принимает значение И хотя бы для одной совокупности значений её свободных переменных и хотя бы одного значения переменной x.
· Формула  xA истинна в данной интерпретации тогда и только тогда, когда в этой интерпретации истинно A.
xA истинна в данной интерпретации тогда и только тогда, когда в этой интерпретации истинно A.
· Если формула A замкнута, то в данной интерпретации A означает некоторое высказывание (нет свободных переменных), следовательно, A истинно либо ложно. Иначе, если A замкнуто, то в любой данной интерпретации либо истинно A, либо истинно 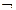 A.
A.
Рассмотрим некоторую пропозициональную форму. Если в пропозициональную форму вместо пропозициональных букв подставить формулы логики предикатов (вместо всех вхождений одной и той же пропозициональной буквы подставлять одну и ту же формулу), получим некоторую формулу, которая называется частным случаем пропозициональной формы. Тогда легко доказать следующее утверждение. Всякий частный случай любой тавтологии истинен в каждой интерпретации.
Опр. Формула логики предикатов называется логически общезначимой, если она истинна в любой интерпретации.
Логическая общезначимость формулы означает, что какую бы ни выбирали область интерпретации и какие бы соответствия не задавали, мы всегда будем получать истинные отношения или высказывания.
Примером логически общезначимых формул, очевидно, являются следующие формулы:  xA→
xA→ 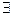 хА ;
хА ;  xA ≈
xA ≈ 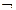
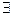 х
х 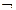 А .
А .
Опр. Формула логики предикатов A называется выполнимой, если существует интерпретация, в которой выполнима A.
Примером выполнимой формулы является приведенная выше формула  xA(x,y, b1).
xA(x,y, b1).
Имеют место следующие очевидные утверждения.
1. Формула A логически общезначима тогда и только тогда, когда формула A не является выполнимой.
2. Формула A выполнима тогда и только тогда, когда формула 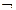 A не является логически общезначимой.
A не является логически общезначимой.
Формулу логики предикатов A называется противоречием, если формула 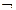 A является логически общезначимой. (Формула A ложна во всякой интерпретации.)
A является логически общезначимой. (Формула A ложна во всякой интерпретации.)
Говорят, что формула логики предикатов A логически влечет формулу логики предикатов B , если в любой интерпретации формула B принимает значение И при каждой совокупности значений свободных переменных (входящих в A и B), при которых формула A приняла значение И. Иначе говорят, что B является логическим следствием формулы A. Формулы A и B логики предикатов называют равносильными (логически эквивалентными), если каждая из них логически влечет другую. Если формулы А и В равносильны, то, как и в логике высказываний, записываем: A ~В.
Следующие теоремы проливают свет на смысл логических связок.
Теорема. Формула A логически влечет формулу B тогда и только тогда, когда формула A→ B логически общезначима.
Теорема. Формулы A и B равносильны (логически эквивалентны) тогда и только тогда, когда формула A≈ B логически общезначима.
Теорема 2.3. Если формула A логически влечёт формулу B и A истинно в данной интерпретации, то в этой же интерпретации истинно и B.
Формула B называется логическим следствием формул А1, А2, Ап, если в любой интерпретации формула B принимает значение И при каждой совокупности значений свободных переменных (входящих в B и А1, А2, ., Ап), при которых одновременно все формулы А1, А2, …, Ап приняли значение И. Иными словами говорят, что B является логическим следствием формул А1, А2,…, Ап.
Замечание. Из приведенных теорем следует, что , если мы применим правило преобразования связанных переменных, то получим логически эквивалентную исходной формулу, в которой уже одна и та же переменная не будет обозначать разные сущности.
При определении формулы исчисления предикатов мы фиксировали полную систему логических связок:( 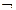 ,→). Так как она полна, то через нее можно выражать остальные функции алгебры логики. Очевидно, что из теоремы Поста следует, что для любой формулы существует логически эквивалентная формула, которая содержит только функции алгебры логики, входящие в фиксированную систему логических связок, использованную при определении формулы. В этом случае говорят, что данная формула имеет нормальную форму.
,→). Так как она полна, то через нее можно выражать остальные функции алгебры логики. Очевидно, что из теоремы Поста следует, что для любой формулы существует логически эквивалентная формула, которая содержит только функции алгебры логики, входящие в фиксированную систему логических связок, использованную при определении формулы. В этом случае говорят, что данная формула имеет нормальную форму.
Опр. Формула исчисления предикатов следующего вида: F=Qx1 Q2 x2… QnxnG, где Qx1, Q2 x2,…, Qnxn – кванторы, а формула G не содержит кванторов, называется формулой в предваренной (приведенной) нормальной форме.
Просто из определения логических функций (конъюнкции, дизъюнкции, импликации и отрицания) сразу следует утверждение.
Теорема. Для каждой формулы логики предикатов длины L в нормальной форме со связками ( 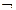 ,→) существует логически эквивалентная (равносильная) ей формула в нормальной форме со связками
,→) существует логически эквивалентная (равносильная) ей формула в нормальной форме со связками 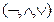 , имеющая длину constL.
, имеющая длину constL.
В [3] приведено доказательство следующей теоремы.
Теорема. Для каждой формулы логики предикатов в нормальной форме со связками ( 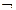 ,→) существует логически эквивалентная (равносильная) ей формула в предваренной нормальной форме.
,→) существует логически эквивалентная (равносильная) ей формула в предваренной нормальной форме.
При этом автор не следит за длиной формул (она его не интересует). Если дословно взять это доказательство и проследить за длинами формул, то мы увидим, что на самом деле в доказано следующая теорема.
Теорема. Для каждой формулы длины L логики предикатов в нормальной форме со связками ( 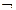 ,→) существует логически эквивалентная (равносильная) ей формула в предваренной нормальной форме длины constL.
,→) существует логически эквивалентная (равносильная) ей формула в предваренной нормальной форме длины constL.
На самом деле весь проведенный экскурс в теорию предикатов нам был нужен для того, чтобы сформулировать следующее утверждение.
Теорема. Для каждой формулы F логики предикатов l(F) существует логически эквивалентная (равносильная) ей формула F* в предваренной нормальной форме длины не более, чем kl(F), где k- некоторая константа.
На самом деле справедливо более точное относительно соотношения длин формул утверждение, но мы даем эту теорему без доказательства, а для ее использования при анализе класса нам достаточно данной формулировки.
Теорема 9.6. "Задача выполнимости булевской формулы с кванторами" PSPACE-полна.
Выше речь шла о задаче выполнимости КНФ, т.е. рассматривалась булевская формула без кванторов. В данном случае речь идет о булевских формулах вида
F(x)=Q1y1…QnynH(y1,…,yn),
где Qi — это либо квантор всеобщности ", либо квантор существования $. По определению, ($xA(x))=(A(0)ÈA(1)), "xA(x))=(A(0)&A(1)). Задача выполнимости булевской формулы с кванторами (ЗВБФК) состоит в ответе на вопрос о существовании набора значений переменных, на которых формула истинна.
Нам нужно построить сведение любого языка LZ из PSPACE к задаче ЗВБФК. Берем МТ для задачи Z и строим по ней игру, как это было показано во второй части доказательства предыдущей теоремы. Затем по этой игре строим МТ, проверяющую результат игры. Ходы игроков кодируем булевскими переменными. Тогда, например, наличие выигрышной стратегии у белых задается условием
$w11$w12…$w1p(|I|)"b11"b12…"b1p(|I|)f(I,w11,…).
Здесь f(I,w11,…) — результат проверки истинности предиката. Эта проверка может быть представлена как вычисление по булевской схеме. В свою очередь схеме однозначно сопоставляется булевская формула.
Таким образом мы получаем квантифицированную булевскую формулу, которая истинна тогда и только тогда, когда I лежит в LZ.
Теорема доказана.
Заметим, что при доказательстве теоремы 9.5 класс PSPACE можно заменить на NPSPACE. То есть справедливо следующее утверждение.
Теорема 9.7. Задача Z лежит в классе NPSPACE тогда и только тогда, когда существует игра с полиномиальным от длины входа числом ходов и полиномиально вычислимым результатом такая, что LZ=Lw.
Первая часть доказательства теоремы 9.5.остается просто без изменения. Для доказательства второй части заметим, что допускающая таблица для недетерминированной МТ будет иметь те же размеры, что и аналогичная таблица в теореме 9.5.
Следствие. PSPACE= NPSPACE.
Классы P и P/poly.
Рассматриваем, как обычно, задачи в форме распознавания. В начале курса мы говорили о возможности двух принципиально разных подходов к анализу понятия «сложность задачи». Один из них был связан с алгоритмом решения задачи Z, второй – со сложностью СФЭ, реализующих булеву функцию fZ, значение которой дает ответ на задачу Z в форме распознавания.
Схема доказательства теоремы Кука позволяет легко установить соответствие между классами P и P/poly.
Действительно, для любой задачи из P можно построить допускающую таблицу ее решения на машине Тьюринга так же, как это сделано выше при доказательстве теоремы Кука. По этой таблице мы построим КНФ полиномиальной длины f, а уже для этой КНФ - схему их функциональных элементов, вычисляющую f. Очевидно, что схема будет содержать полиномиальное число вершин. Таким образом, справедливо следующее утверждение.
Теорема 9.1. P Í P/poly.
А что будет, если Z 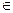 P/poly? Оказывается, что класс P/poly шире класса P. Это связано с тем, что существуют алгоритмически неразрешимые проблемы. В курсе дискретной математики вам о них, наверное, рассказывали.
P/poly? Оказывается, что класс P/poly шире класса P. Это связано с тем, что существуют алгоритмически неразрешимые проблемы. В курсе дискретной математики вам о них, наверное, рассказывали.
Приведем пример, который, по сути, является известным со времен античности парадоксом брадобрея. В деревне есть брадобрей, который бреет всех, кто не бреется сам. Попробуйте ответить на вопрос, бреет ли он самого себя. При любом ответе получается противоречие.
Облачим теперь этот парадокс в «математическую форму». Проблема остановки (halting problem) состоит в том, чтобы ответить на вопрос (мы о нем говорили выше, когда давали определение машины Тьюринга): остановится или зациклится данная машина Тьюринга T на данном входе x? Оказывается, что, как и в случае брадобрея, любой ответ приводит к противоречию. То есть не существует машины Тьюринга, которая решает проблему остановки.
Теорема. Проблема остановки алгоритмически неразрешима.
Доказательство. От противного. Пусть такая машина T* существует. Тогда на входе (T,x) она выдает ответ «да», если машина Т останавливается на этом входе, и «нет» в противном случае. (Здесь Т – слово в алфавите А, являющееся описанием машины Т). Тогда по Т* можно построить машину Тьюринга T’(x), которая в случае, если T*(x,x)=”да”, начинает двигать головку в одну сторону и зацикливается, а в случае T*(x,x)=”нет” она останавливается. Что в этом случае будет означать T’(T’)? Остановится или нет машина на этом входе? Если «да», то это означает, что T*(T’)= «нет», т.е. T’ не должна останавливаться на T’. Если «нет», то это означает, что T*(T’)= «да», т.е. T’ должна останавливаться на T’.
Получили противоречие
Теорема доказана.
Рассмотрим функцию натурального аргумента f(n), принимающую значения 0 или 1. Можно показать, что вычисление такой функции может быть алгоритмически неразрешимой проблемой, т.е. не входит такая задача ни в какой класс сложности, а не только в класс P. Рассмотрим теперь предикат Af(x)=f(|x|). Для любого фиксированного n предикат равен константе. А константе сопоставляется СФЭ, сложность которой тоже равна константе. Поэтому Af(x) 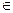 P/poly, но его вычисление может быть алгоритмически неразрешимой проблемой.
P/poly, но его вычисление может быть алгоритмически неразрешимой проблемой.
Конечно, все это связано с тонкостями определений математических объектов и тем, что при вычислении предикатов основная сложность может лежать не в логических операциях, а в вычислении термов, от которых зависит предикат. Это вычисление связано с интерпретацией и допускает наличие в качестве аргумента предиката произвольной, сколь угодно сложновычислимой функции.
Результатом этого рассмотрения является следующая простая теорема (см. [6]).
Пусть задача Z в форме распознавания эквивалентна вычислению булевой функции f. Суть в том, что с ростом числа переменных n=1,2,… мы имеем последовательность формул fn и схем Sn для этой функции. И именно свойства такой последовательности для нас выжны.
Теорема. Функция (задача) f 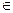 P тогда и только тогда, когда f
P тогда и только тогда, когда f 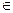 P/poly и существует машина Тьюринга, которая за полиномиальное от длины входа n время строит СФЭ для fn.
P/poly и существует машина Тьюринга, которая за полиномиальное от длины входа n время строит СФЭ для fn.
Для доказательства заметим следующее. Теорема Кука дает конструктивный метод построения СФЭ полиномиального по входу размера за полиномиальное по входу время для функции f 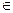 P. Т.е. в этом случае f
P. Т.е. в этом случае f 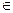 P/poly и за полиномиальное от длины входа n время строястя СФЭ для fn.
P/poly и за полиномиальное от длины входа n время строястя СФЭ для fn.
И наоборот, если f 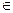 P/poly и существует Т - машина Тьюринга, которая для каждого отдельного n за полиномиальное от длины входа время по n строит СФЭ Sn для fn. Вычислений значения функции по этой схеме тоже потребует не более, чем полиномиального времени.
P/poly и существует Т - машина Тьюринга, которая для каждого отдельного n за полиномиальное от длины входа время по n строит СФЭ Sn для fn. Вычислений значения функции по этой схеме тоже потребует не более, чем полиномиального времени.
Грубо говоря, с точностью до «разницы в определениях» двух подходов: алгоритмического и схемного, можно представлять себе классы P и P/poly достаточно близкими. Про соотношение классов P и NP мы ничего не знаем. А вот на вопрос, как соотносится класс P/poly с классом всех СФЭ, ответ дает теорема Лупанова. Почти все схемы имеют экспоненциальную сложность 2n/n, т.е. множество функций (задач в форме распознавания), имеющих СФЭ полиномиального размера , пренебрежимо мало. Этот результат создал иллюзию безысходности в области исследований по алгоритмической сложности в 1960-е годы. На этом фоне результат Кука (1971 год) явился определенным идеологическим прорывом в том смысле, что он обратил внимание исследователей на небезнадежность решения задач, принадлежность которых к классу NPC не удалось доказать после достаточно серьезных усилий квалифицированных специалистов. И хотя таких задач было решено немного (пионером здесь является Л.Г.Хачиян , решивший за полиномиальное время задачу линейного программирования), но каждое из таких решений явилось фундаментальным достижением в математике.
Некоторые результаты
Обозначим через SPACE(f(n)) класс задач (языков), для которых существует МТ, работающая на памяти с объемом, ограниченным f(n).
Аналогично NSPACE(f(n)) класс задач (языков), для которых существует НМТ, работающая на памяти с объемом, ограниченным f(n).
Приведем без доказательства следующее утверждение, уточняющее некоторые из вышеприведенных.
Теорема 9.7. NSPACE(f(n))ÍSPACE(f(n)2).
Дата: 2019-07-30, просмотров: 359.