Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Э.Н.Гордеев

 

ВВЕДЕНИЕ В ТЕОРИЮ СЛОЖНОСТИ АЛГОРИТМОВ.

Учебное пособие

 по дисциплине «Математическая логика и теория алгоритмов».

 

 

Москва

(С) 2016 МГТУ им. Н.Э. БАУМАНА

 

УДК 519.7

Гордеев Э.Н.

Введение в теорию сложности алгоритмов. Электронное учебное издание. - М.: МГТУ имени Н.Э. Баумана, 2016. 128 с.

Издание содержит конспект лекций по курсу «Математическая логика и теория алгоритмов», предусмотренного учебным планом МГТУ им. Н.Э.Баумана. Представлены формальные модели алгоритмов, рассмотрены различные подходы к понятию сложность задачи. Описаны наиболее известные классы сложности задач. Приведены примеры исследования сложности известных задач.

Для студентов факультета «Информатики и систем управления» МГТУ имени Н.Э. Баумана.

 

Рекомендовано учебно-методической комиссией НУК «Информатики и систем управления» МГТУ им. Н.Э. Баумана

 

Гордеев Эдуард Николаевич

 

ВВЕДЕНИЕ В ТЕОРИЮ СЛОЖНОСТИ АЛГОРИТМОВ.

 

© 2016 МГТУ имени Н.Э. Баумана

 

 

Оглавление

Предисловие. 6

1. Введение. 6

1.1. Некоторые необходимые определения и понятия. 6

2. Задачи, алгоритмы.. 8

2.1. Задача. 9

2.2. Алгоритм. 16

3. Нормальные алгорифмы Маркова (НАМ). 21

4. Машины Тьюринга. 23

4.1. Одноленточная МТ. 23

4.2. Многоленточная МТ. 26

4.3. Недетерминированная МТ. 27

4.4. Оракульная МТ. 28

5. Равнодоступная адресная машина (РАМ) и некоторые другие подходы. 29

6. Сравнение различных формальных схем. 34

6.1. Кодировки входных данных. 34

6.2. О мерах сложности. 36

6.3. Теоремы сравнения. 40

6.4. Полиномиальные и неполиномиальные оценки сложности. 43

7. Сложность алгоритмов некоторых задач. 45

7.1. Задача нахождения максимального числа. 46

7.2. Задача сортировки. 46

7.3. Задача о камнях. 47

7.4. Простота числа. 47

7.5. Задача о кратчайшем (минимальном) остове (остовном дереве). 48

7.6. Задача коммивояжера. 50

7.7. Задача о комивояжере и динамическое программирование. 51

7.8. Задача о кратчайшем пути. 52

7.9. Задача о выполнимости КНФ (КНФ-выполнимость) 53

8. Схемы из функциональных элементов. Схемная сложность. 53

8.1. Схемы из функциональных элементов. 53

8.2. Оценки сложности СФЭ. 56

9. Теория NP-полноты.. 62

9.1. Классы P и NP. 62

9.2. Сводимость задач. 64

9.2.1. Смысл сводимости. 64

9.2.2. Полиномиальная сводимость. 66

9.2.3. Сводимость по Тьюрингу. 68

9.3. Теорема Кука. 70

9.4. Структура класса NP и некоторые выводы.. 77

10.   Иерархия сложности . 81

10.1.   Классы NP и co-NP. 81

10.2.   Классы P-SPACE и NP-SPACE. 84

10.2.1.   Классы сложности P-SPACE и NP-SPACE. 84

10.3.   Логика предикатов и PSPACE –полные задачи. 92

10.4.   Классы P и P/poly. 105

10.5.   Некоторые результаты.. 109

11.   Подходы к решению NP-полных задач. 109

11.1.   NP-полнота в сильном смысле. Псевдополиномиальные алгоритмы 110

11.2.   Приближенные алгоритмы.. 112

11.3.   Полиномиально-разрешимые частные случаи NP-полных задач. 114

11.4.   Методы направленного перебора. 115

12.   Коммуникационная сложность. 118

Заключение. 123

13.   Задачи и вопросы для самопроверки по курсу «Математическая логика и теория алгоритмов». 123

13.1.   Задачи. 123

13.2.   Вопросы. 126

14.   Рекомендованная литература. 128

 

Предисловие.

Данный текст представляет собой  конспект лекций по курсу «Математическая логика и теория алгоритмов», предусмотренного учебным планом МГТУ им. Н.Э.Баумана для студентов кафедры ИУ-8. Он содержит самые базовые классические результаты по теории сложности алгоритмов, а также необходимые для изложения материалы по математической логики, которые не вошли в читавшиеся ранее курсы дискретной математики и основ информатики. Представлены формальные модели алгоритмов, рассмотрены различные подходы к понятию сложность задачи. Описаны наиболее известные классы сложности задач. Приведены примеры исследования сложности известных задач.

Излагаемый материал необходим для последующих курсов, в особенности, курса «Алгоритмы и структуры данных» и «Теория принятия решений».

Введение

1.1. Некоторые необходимые определения и понятия.

При сравнении скорости роста двух неотрицательных функций f(n) и g(n) удобно использовать следующие обозначения.

Говорят, что функция g(n) f(n)-ограничена, если g(n)£f(n). Если f(n) - полином, то функция g(n) называется полиномиально ограниченной, а если экспонента – экспоненциально ограниченной.

Будем говорить, что f(n)= O(g(n)), если существуют такие положительные константы c и N, что f(n)≤c g(n)для всех n>N.

В этой же ситуации можно использовать и обозначение g(n)=Ω(f(n)). Например, справедливы соотношения log₂ n = O(n), n = Ω(log₂ n), n = O(2ⁿ).

Будем говорить, что f(n)= o(g(n)), если .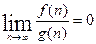

Если f(n)= O(g(n)) и O(f(n))= g(n) , то это будем обозначать через f(n)=Θg(n).

Для числа x  целые числа [x] и ]x[ - это целые части числа с недостатком и с избытком.

Опр. Алфавит A – это конечный или бесконечный набор символов: A={a₁,a₂,…,a_n,…}.

Опр. Слово – это конечный упорядоченный набор символов алфавита.

Выделяется специальное пустое слово 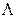(слово, не содержащее символов).

Пусть 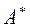 – множество всех слов в алфавите .

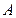Опр. Язык L – это подмножество . ( ).

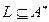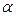
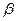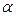Опр. Конкатенация  слов  и .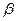

.

Число сочетаний (без повторений) из n элементов по k элементов обозначим через 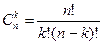. Число сочетаний с повторениями из n элементов по k элементов обозначим через .

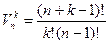Если не оговорено обратное, вместо log₂n будем писать log n.

Простой граф с множеством вершин V, |V|=n, и множеством ребер E, |E|=m, будем обозначать через G=(V,E). Ориентированность графа будет оговариваться отдельно.

Булевы переменные - это переменные, принимающие значения из множества B={0,1}. Множество n-мерных векторов из нулей и единиц называется булевым кубом и обозначается Bⁿ. Очевидно, что число вершин этого куба равно 2ⁿ.

Отображение f: Bⁿ®B называется булевой функцией. Число булевых функций от n переменных равно

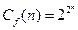
Примеры известных булевых функций: конъюнкция (&), дизъюнкция (È), отрицание (Ø), импликация (®), сложение по модулю «два» (Å), эквивалентность ( 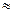) и пр.

Табличный способ задания функции представляет собой таблицу размером 2ⁿx(n+1). В последнем столбце таблице записаны значения функции на каждом из 2ⁿ возможных наборах значений переменных. Сами эти наборы записаны в первых n клетках каждой строки.

При работе с булевыми функциями мы иногда будем заменять значок логического умножения &  значком 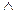, обычной точкой (произведением) или не писать его вовсе.

Задачи, алгоритмы

В любой математической дисциплине, которая претендует на наличие собственного взгляда на "математическую" проблематику, исходные понятия не определяются математическим языком. Обычно, речь идет об "интуитивных" объектах, сущность которых может обсуждаться за пределами математики.

В этом курсе мы тоже будем иметь дело с несколькими лишь интуитивно определяемыми понятиями. Важнейшие из них - задача и алгоритм. Сразу оговорим очевидное. Для описания базовых понятий раздела науки используются те же слова, которые применяются и на бытовом уровне. Но в науке они становятся терминами и приобретают особый смысл. В лекции иногда трудно избежать ситуации, когда одно и то же слово используется и в качестве термина, и в качестве обиходного. В тексте при подозрении на двусмысленное понимание для терминов будет использоваться курсив, а для обиходных – кавычки, а там, где двусмысленность при разумном понимании невозможна – обычный шрифт.

Задача

Начнем с обсуждения первого из упомянутых понятий – понятия задача. При описании базовых понятий или аксиоматики используется три способа: аналогия, пример и расчленение «менее элементарных» сущностей на совокупность «более элементарных». Пойдем и мы по этому пути.

Наш курс тесно связан с двумя математическими дисциплинами: математической логикой и дискретной математикой. Поэтому самая простая идентификация понятия может быть дана по аналогии. Вспомним то, что имелось в виду под задачей в этих дисциплинах. В нашем курсе мы будем иметь дело примерно с тем же самым.

Например, в [1] определение задачи вообще не дается, считается, что оно «интуитивно очевидно». В [2] под задачей понимается «некоторый общий вопрос, на который следует дать ответ». При этом «задача содержит несколько параметров или свободных переменных, конкретные значения которых не определены».

В [4] под задачей понимается «выбор наилучшей конфигурации или множества параметров для достижения некоторой цели». При этом задачи делятся на непрерывные и комбинаторные. «В непрерывных задачах обычно отыскивается множество действительных чисел или даже некоторая функция; в комбинаторных задачах – некоторый объект из конечного или возможно бесконечного счетного множества». Другими словами, задача оптимизации – это пара ( F, c) , где F – произвольное множество, область допустимых точек, а – c функция стоимости, отображающая элементы  F на множество действительных чисел. Требуется найти такую x* точку из F, на которой значение функции c(x*) обладает определенным свойством, например, минимально, максимально и пр.

Теперь займемся «расчленением» сущностей, приведенных выше. Задачи, рассматриваемые в нашем курсе, это, в подавляющем большинстве, задачи комбинаторные или дискретные. Уже само слово комбинаторный относится к упомянутому выше множеству F. Вернее, к способу его задания. Мы видим, что при таком задании с задачей обычно связывается два объекта: множество параметров и структура связей между ними. Параметры – «язык» для описания условий задачи. Структура связей содержит нечто, позволяющее описать  F , а также сформулировать вопрос (см. [2])  или требование к c(x*) трактуемое как вопрос, свойство функционала и пр. (См. [4]).

В теории сложности термин задача сразу же разбивается на два термина: индивидуальная задача и массовая задача. Это связаны со способом задания параметров. Массовая задача предполагает описание множества параметров, а индивидуальная задача возникает, при фиксации значений этих параметров.

Понятие формы задачи, грубо говоря, возникает в связи с возможностью "незначительно" модифицировать вышеупомянутые форму вопроса или свойство c(x*).

Поясним сказанное на примерах. Но эти примеры будут носить не только иллюстративный характер. В их тексте мы дадим и разъясним многие общие (выходящие за рамки примера) понятия, которые в дальнейшем будут использоваться.

Многие из этих примеров будут неоднократно упоминаться в дальнейшем, поэтому для упрощения ссылок на них мы дадим приведенным ниже задачам краткие названия.

Пример 1. (Поиск максимального числа). Заданы N целых чисел: a₁,…a_N. Требуется найти максимальное из них.

На примере этой простейшей задачи постараемся подробно проанализировать условие задачи.

Здесь параметрами являются числа: N и a₁,…,a_N. Правильнее представлять их в виде объектов, имеющих числовые значения. Это означает, что количество сущностей, между которыми при формулировке и решении задачи будут устанавливаться связи, равно 2N+2. Одна сущность предназначена для описания мощности множества сравниваемых чисел, другая – представляет собой числовое значение этой мощности (оно равно N), N сущностей предназначено для идентификации сравниваемых объектов. Эта идентификация достигается путем индексации: 1,…,N. Остальные N: a₁,…a_N – это веса (значения) проиндексированных объектов. В дальнейшем для сущностей, принимающих числовые значения, будем использовать понятие параметр, а для остальных – объект. Они не равноправны: сначала должны быть заданы объекты, а затем уже – параметры. Это означает, что задание параметра возможно после задания объекта. Можно также задать все объекты и лишь часть параметров или задать часть объектов, а затем определить параметры, с ними связанные.

В нашем примере связи на множестве объектов строятся через их параметризацию с использованием отношения сравнения чисел. Задание (свойство c(x*))в данном случае состоит в нахождении объекта, значение которого максимально. Если всем этим объектам и параметрам присвоены конкретные  значения, то получается индивидуальная задача. В ситуации, когда речь идет о произвольных значениях объектов, мы имеем дело с массовой задачей. Заметим, что роли параметра N и параметров a₁,…a_N неодинаковы, т.е. можно говорить о множествах индивидуальных задач, получаемых из массовой задачи путем фиксации параметра N.

Уже такая простейшая задача позволяет проиллюстрировать понятие формы задачи. В данном случае можно говорить о задаче в форме оптимизации. Подобная форма возникает тогда, когда речь идет об экстремуме некоторого функционала на множестве исходных параметров задачи.

Задача в вычислительной форме получается при следующей модификации вопроса: "Требуется найти величину максимального из данных чисел". То есть здесь не нужно указывать сам объект, а только его числовое значение. Казалось бы, это условие не очень важное, но для ряда задач трудности решения их в оптимизационной и вычислительной формах различаются весьма существенно.

Другой распространенный тип задач - задачи в форме распознавания. В нашем случае для подобных задач добавляется еще один параметр B, а задание выглядит следующим образом. Требуется ответ на вопрос, существует ли среди объектов a₁,…a_N такой, значение которого не меньше, чем B? При этом, вообще говоря, не требуется ни указывать сам объект, ни его значение.

В последнем случае мы видим, что речь идет не только о форме задания, но и изменении множества параметров. То есть задача уже другая, но "близкая" к исходной. Это соответствует интуитивному представлению о том, что «незначительное» изменение в формулировке условия может приводить к «незначительному» изменению самой задачи.

Что значит незначительно? Как при этом меняется трудность решения? Этими вопросами мы тоже будем заниматься в нашем курсе.

Пример 2. (Разложение на множители). Дано натуральное число N. Требуется разложить его на простые множители.

Параметром здесь является само число (значение объекта). При его фиксировании возникает индивидуальная задача. Если говорить о форме задачи, то она явно не оптимизационная, да и вычислительной не является, хотя в широком смысле под вычислением в данной задаче можно понимать нахождение всех простых делителей с их кратностями. Близкая к данной задача в форме распознавания  состоит в определении простоты числа (задача о простоте числа).

Пример 4. (Задача о гамильтоновом цикле). Дан простой неориентированный граф G c N вершинами. Требуется узнать, существует ли в нем гамильтонов цикл. (Гамильтоновым называется цикл в графе, который проходит через каждую вершину графа ровно по одному разу.)

Набор исходных параметров - это число N и множество ребер графа, задаваемых как пары разных чисел из множества 1,…,N. Понятие гамильтонова цикла задает связь на множестве параметров.

Задача представлена в форме распознавания. Вычислительную и оптимизационную форму здесь искать малоинтересно. Но возникает еще одна форма - перечислительная. В этой задаче требуется найти число различных гамильтоновых циклов графа.

В дальнейшем будем, как правило, называть эту задачу просто: "гамильтонов цикл".

Пример 5. (Задача о коммивояжере.) Дан граф G c N вершинами, ребрам которого приписаны веса c_ij. Требуется найти гамильтонов цикл экстремальной длины. (Длина гамильтонова цикла может задаваться по-разному. В большинстве случаев – это сумма длин входящих в цикл ребер. Если не оговаривается обратное, то именно эта ситуация и имеется в виду. Но за длину можно брать и максимальный (минимальный) вес входящего в него ребра, и более сложный функционал от длин ребер. Наиболее распространенный случай, когда под экстремумом понимается минимум. Если же экстремум трактуется как максимум, то это оговаривается отдельно. Такие задачи называются задачами коммивояжера на максимум).

Можно считать, что граф полный (отсутствующим ребрам приписать специальным образом выбранные «большие» значения). Тогда набор исходных параметров определяется числом N и матрицей весов ребер С=(c_ij). Индивидуальная задача получается из массовой фиксированием этих параметров.

В дальнейшем будем называть эту задачу просто "коммивояжер".

В формулировку задания входит понятие гамильтонова цикла, которое и задает связь на множестве параметров.

В вышеупомянутом варианте мы имеем задачу в форме оптимизации. Вычислительный вариант задачи состоит, например, в нахождении длины минимального гамильтонова цикла. В случае задачи на минимум в варианте распознавания задается еще число B и требуется ответить на вопрос, существует ли гамильтонов циклы с длиной, не превосходящей B.

Можно получить еще один вариант - перечислительный. Он состоит в нахождении количества минимальных гамильтоновых циклов.

Приближенный вариант без оценки точности состоит в нахождении гамильтонова цикла, который отличается от минимального "незначительно". При этом в понятие «незначительно» никакого формального смысла не вкладывается.

Приближенный вариант с оценкой точности может выглядеть следующим образом. Требуется для заданного числа k найти гамильтонов цикл, превосходящий минимальный не более чем в k раз.

Пример 6. (Задача о выполнимости КНФ.) Задана булевская функция F от N переменных в виде конъюнктивной нормальной формы K. Требуется определить, существует ли такой набор значений переменных, на котором функция обращается в единицу.

Здесь мы имеем задачу в форме распознавания. Исходными параметрами являются N и K. Что касается задания связей на множестве исходных параметров, то их можно проиллюстрировать следующим образом. Всех конъюнкций от N переменных 3^N. Обозначим это множество через Q(N). Индивидуальная задача получается из массовой путем фиксирования числа N и подмножества M из Q(N).

В дальнейшем будем называть эту задачу просто "КНФ-выполнимость".

Задача о клике ("клика") состоит в нахождении максимального (по числу вершин) полного подграфа K заданного графа G. Задача о кратчайшем остове ("остов") состоит в нахождении минимального (например, по сумме длин входящих ребер) остовного дерева T графа G, ребрам которого приписаны веса. Само название Задача о кратчайшем пути ("кратчайший путь") между двумя фиксированными вершинами графа уже все определяет. Задача об изоморфизме графов ("изоморфизм графов") состоит в определении изоморфизма пары заданных графов.

Алгоритм

Если с понятием задачи все теперь более или менее понятно, то вот с понятием алгоритма дело обстоит сложнее. Работа в этом направлении породила не только теорию сложности или столь распространенные сейчас компьютеры, но и разделение математики, в которой на некоторое время остро стал вопрос о конструктивности. Но это тема отдельного большого разговора.

Итак, есть задача. Встает вопрос о ее решении. Какую бы форму задачи мы не взяли, решение задачи предполагает нахождение некоторого объекта или его свойства. В случае индивидуальной задачи по исходному набору параметров (объектов и их значений) требуется найти некоторый объект (если речь идет об оптимизационной форме), число (если речь идет о вычислительной или перечислительной форме), вариант (один из двух: "да" или "нет", если речь идет о задаче в форме распознавания).

В жизни мы отнюдь не всегда для решения задач используем "алгоритмы". (Скорее, почти никогда их не используем). Действительно, мы можем найти объект, угадав его или используя наш опыт.

В этих случаях процесс нахождения состоит из двух важных этапов. Сначала в результате угадывания или опыта мы в качестве предполагаемого решения выбираем некоторый объект. Затем мы убеждаемся, что данный объект является требуемым решением задачи. Назовем первый этап этапом предложения, а второй - этапом проверки.

Если мы имеем задачу в форме распознавания, то нам не важна "логика" действий на первом этапе. Действительно, мы просто строго проверяем объект на наличие требуемого свойства. Например, в задаче о камнях мы считаем сумму весов предложенного подмножества объектов, в задаче о гамильтоновом цикле проверяем предложенное подмножество ребер на "гамильтоновость".

В том случае, когда правильное предложение возникает в результате отгадки, интуиции, опыта и пр., принято объединять все эти процессы, вводя понятие оракула. То есть оракул- это абстрактная сущность, которая мгновенно, без затраты ресурсов (памяти, времени и т.п.) способна предоставить предложение, возможно,  нуждающееся в проверке. Конечно, его можно проверить, но оракул на то и оракул, чтобы не ошибаться.

Для задач в форме оптимизации тоже может иметь место этап предложения, но этап проверки эквивалентен исходной задаче. В жизни мы можем его заменить верой или интуицией, но в математике требуется нечто иное. Требуется процедура, не зависящая от производящего ее субъекта, которая бы абсолютно достоверно позволяла находить (проверять) требуемый в условии задачи объект.

Это и есть интуитивное представление алгоритма. В [2] например, оно звучит так. Алгоритм - это общая, выполняемая шаг за шагом процедура решения задачи. Прилагательное "общая" отвечает за автоматизм, независимость от субъекта, использующего алгоритм. Требование выполнения работы "шаг за шагом" здесь не ограничивает тип алгоритма (например, не отбрасывает параллельные или вероятностные алгоритмы), а лишь указывает на предсказуемость и проверяемость самой процедуры решения.

Во многих попытках дать определение алгоритма используются понятия "искусство" и "автоматизм" (машинное исполнение). При этом первое как раз должно отсутствовать в этом самом "алгоритме", а второе должно его характеризовать.

Формализация понятия "алгоритм" необходима также из-за "несимметричности" ответа на вопрос, существует ли алгоритм для решения задачи Z?

Действительно, ответ "да" может быть получен путем построения некоторой процедуры решения, которая укладывается в "интуитивное" понятие алгоритма. Такие процедуры и строились в процессе всей истории математики, когда формальным построениям самого понятия алгоритм внимания не уделялось. Если для некоторой задачи не могли построить метода решения, то это списывалось на недостаток умения.

Имея лишь интуитивное представление об алгоритме, нельзя доказать, что этого самого алгоритма не существует.

В 30-е годы стали появляться первые формальные схемы алгоритма. Эти схемы были предназначены исключительно для теоретических исследований. С некоторыми из них мы познакомимся здесь. Речь пойдет, например, о машинах Тьюринга (МТ), нормальных алгорифмах  Маркова (НАМ) и др.

Алгоритм производит некоторые "действия" с объектами и параметрами, начиная с исходных условий задачи (входные условия, вход). Во всех известных формальных схемах этот вход как-то задается. В самом общем случае можно считать, что это задание выглядит в виде слова в некотором алфавите.

Напомним, что множество (конечное или бесконечное) символов называется алфавитом A. Слово P в алфавите A - любая конечная последовательность символов алфавита.

Если множество символов одного алфавита является подмножеством символов другого, то первый называется подалфавитом второго. А второй - надалфавитом первого.

Пусть A - подалфавит некоторого алфавита B. Слово, состоящее из символов алфавита A, будем называть словом в алфавите A. Слово, состоящее из символов алфавита B, будем называть словом над алфавитом A.

Заметим, что достаточно ограничиться алфавитом из двух символов, например, 0 и 1. Любой символ a_i алфавита A={a₁,…,a_n,…} может быть закодирован следующим образом: a_i =011...10, где 1 повторяется n раз.

В известных формальных схемах (формализмах) "алгоритм" можно представить как некоторое пошаговое преобразование одних слова в другие, начиная с входа x₁,…,x_n = X. В результате последнего шага таких преобразований получаем некоторое выходное слово Y. Его можно трактовать как результат работы алгоритма. Задавая буквы входного алфавита числовыми последовательностями, можно считать, что речь идет о вычислении функции f(x₁,…,x_n)=f(X)=Y.

Обратим внимание на употребление понятия эквивалентности в связи с наличием нескольких возможных представлений (кодировок, способов записи) входных объектов.

Два выражения (кодировки) B и C считаются эквивалентными B»C в двух случаях: либо оба выражения не определены (бессмысленны), либо определены и обозначают один и тот же объект.

Будем говорить, что алгоритм Á является алгоритмом в алфавите A, если он переводит слова x₁,…,x_n в алфавите A в слова f(x₁,…,x_n) в алфавите A.

Будем говорить, что алгоритм Á является алгоритмом над алфавитом A, если он переводит слова x₁,…,x_n над алфавитом A в слова f(x₁,…,x_n) над алфавитом A.

При этом алгоритм Á может работать не с любыми словами алфавита. Множество тех слов, к которым он применим, назовем областью действия алгоритма Á, а результат применения алгоритма Á к слову P обозначим через Á (P). При этом сам алгоритм не обязан распознавать слова из своей области действия.

Рассмотрим два алгоритма Á и Â над алфавитом A.

Если Á(P)»Â(P) для любого слова P в алфавите A, то эти алгоритмы называются вполне эквивалентными относительно A.

Если Á(P)»Â(P) для любого слова P в алфавите A такого, что хотя бы одно из выражений Á(P) или Â(P) определено и является словом в алфавите A, то эти алгоритмы называются эквивалентными относительно A.

Рассматриваемые ниже формальные подходы к понятию алгоритма заслужили внимание благодаря гипотезам типа тезиса Черча.

Этот тезис говорит об эквивалентности широкого неформально и смутного понятия "интуитивный алгоритм" узкому и весьма замысловатому на первый взгляд формализму типа алгорифма Маркова (МТ) или машины Тьюринга. Утверждается, что для любой задачи, для которой существует «интуитивный» алгоритм решения, можно, например, построить МТ, которая будет решать эту задачу.

Рассмотрим теперь данные формализмы подробно. Заметим, что алгоритм может предназначаться как для решения массовой, так и для решения индивидуальной задачи. (Например, алгоритм сложения двух чисел и алгоритм сложения 5 и 2). Конечно, мы изначально предполагаем, что алгоритм должен решать массовую задачу.

Сделаем одно замечание. Во всех перечисленных ниже формальных подходах алгоритм имеет дело с преобразованием одних слов в другие. То есть, условие задачи Z можно рассматривать как слово в некотором алфавите A. Обозначим все множество слов этого алфавита через A*. Подмножество слов алфавита назовем языком. Обратим внимание, что в содержательном смысле не все слова алфавита являются условиями индивидуальных задач из Z.

Особенно удобно ставить некоторый язык из A* в соответствие задачам в форме распознавания. В этих задачах в качестве решения возможно два варианта: 1 ("да") или 0 ("нет"). Таким образом, задаче Z в форме распознавания можно сопоставить язык L_Z, содержащий в качестве слов все слова из A*, которые являются условиями индивидуальных задач с ответом "да".

Машины Тьюринга

Согласно тезису Черча любые две формальные схемы, описывающие понятие алгоритма должны быть эквивалентны друг другу.

Здесь мы рассмотрим еще одну, пожалую самую сегодня популярную из таких схем - машину Тьюринга. Подобно предыдущему формализму она предназначается для преобразования некоторого одного слова P в заданном алфавите в другое слово Q.

Заметим, что существует несколько разновидностей МТ. Более того, даже для одного и того же типа МТ определения могут варьироваться. Это может быть связано с мелкими техническими удобствами, а также с попытками не загромождать формализма "очевидными" тонкостями.

Одноленточная МТ

Начнем с самого простого объекта - одноленточной детерминированной МТ. Она представляет собой пятерку {S, A, F, q₀, d}, где S={q₁,…q_k} - конечное множество, элементы которого называются состояниями, A={a₁,…,a_n} - алфавит, FÍS. Элементы F называются конечными состояниями, выделено начальное состояние q₀ и схема переходов машины Тьюринга d. Каждый такой переход еще называется командой, а вся схема (список команд) представляет собой частично определенное отображение из S´A®S´A´{L, R, St}. Здесь {L, R, St } - множество из трех элементов, смысл которых ниже поясняется.

Опишем теперь механизм работы МТ. На двусторонней бесконечной ленте, разбитой на ячейке, начиная с некоторой ячейки, записано входное слово P (по одному символу в каждой ячейке). Имеется еще один объект - "головка" МТ, который характеризуется наличием определенного приписанного ей состояния и умением читать и писать.

Работа МТ состоит из последовательности тактов.

В начальный момент времени головка обозревает ячейку ленты, в которой записан первый символ входного слова, и находится в начальном состоянии.

Вообще, положение головки, ее состояние и запись на ленте полностью описывают конфигурацию МТ в данный момент времени. Поэтому конфигурацией МТ и называется слово v₁…v_kq_jv_k+1…v_m. Эта запись свидетельствует о том, что в данный момент времени головка МТ находится в состоянии q_j и обозревает ячейку ленты, в которой записан символ v_k+1. Все же слово, записанное к этому моменту на ленте, имеет вид v₁…v_kv_k+1…v_m.

Каждой конфигурации K=v₁…v_kq_jv_k+1…v_m однозначно сопоставляется пара конфигурации q_jv_k+1и слово конфигурации v₁…v_kv_k+1…v_m.

Такт работы представляет собой переход из одной конфигурации к другой. Этот переход осуществляется путем выполнения некоторой команды q_ia_j ®q_ra_t{Z}. (Пару q_ia_j назовем левой частью команды q_ia_j®q_ra_t{Z}, а тройку q_ra_t{Z} - правой частью этой команды.) Если пара конфигурации не является левой частью ни одной из команд, то МТ останавливается и процесс ее работы заканчивается.

Если же такая команда q_ia_j ®q_ra_t{Z} найдена, то это означает, что перед выполнением данного такта МТ находилась в состоянии q_i, обозревала ячейку с символом a_j, а после выполнения данного такта она перешла в состояние q_r, в ранее обозреваемой ячейке появился символ a_t. Z имеет одно из трех значений L, R, St. В первом случае головка сдвинулась на данном такте на одну ячейку влево, во втором - вправо, в третьем - осталась на месте. Если q_r является конечным состоянием, то процесс работы МТ заканчивается и МТ останавливается. В противном случае для вновь полученной конфигурации ищется команда, правая часть которой совпадает с парой конфигурации, и процесс продолжается.

Так как каждая команда определяется однозначно, то, в отличие от НАМ, порядок команд в списке не имеет значения.

Переход от конфигурации K_i к конфигурации K_j в результате выполнения некоторого такта работы МТ обозначим через K_iú¾K_j. Если существует такая последовательность команд, что в результате их выполнения МТ перешла из конфигурации K_i к конфигурации K_j, то эту ситуацию обозначим через K_i÷ÞK_j.

Заметим, что МТ может зацикливаться. Это довольно тонкий момент в данном формализме, который восходит к тому факту в определении алгоритма, согласно которому алгоритм не обязан сам распознавать слова из своей области действия. Конечно, если мы требуем, чтобы перед началом работы была проведена проверка на соответствие входного слова области действия, то никакого зацикливания не может быть, так как уже на стадии проверки будут отсеяны те слова, на которых алгоритм не может корректно работать (слова, которым он не применим). Если же такой предварительной стадии нет, то она может быть заменена предположением о том, что у нас есть некоторый механизм идентификации зацикливаний. То есть, мы можем различать три ситуации: МТ остановилась и завершила свою работу; МТ находится в процессе работы, совершив некоторой количество переходов, и готовится к очередному такту работы; МТ зациклилась, т.е. будет работать и никогда не остановится.

Если МТ на входном слове P за конечное число тактов останавливается, то говорят, что она применима к этому слову. Последовательность конфигураций от начальной до конечной называется вычислением МТ на слове P.

В отличие от НАМ в данном формализме присутствуют такие понятия как: читающая и пишущая головка, обозреваемая ячейка, сдвиги вправо и влево и пр. Все это с точки зрения формальной схемы интуитивного понятия "алгоритм" также нуждается в формализации. Она более или менее очевидна, особенно с точки зрения людей, знакомых с азами компьютерной техники. (Заметим, что Тьюринг предложил свой формализм в 1935 году, когда о компьютерах еще и речи не было). Предположим, что все эти детали определены, и мы получили некоторый алгоритм Â_T,C. Он работает в алфавите C, C является надалфавитом алфавита A машины Тьюринга Т. А для любых слов P и Q в алфавите С соотношение Â_T,C(P)=Q выполняется тогда и только тогда, когда существует такое вычисление на машине Тьюринга Т такое, что оно начинается с конфигурации q₀P и заканчивается конфигурацией R₁q_iR₂, где R₁R₂=Q.

Вообще же произвольный алгоритм Á в алфавите D называется вычислимым по Тьюрингу тогда и только тогда, когда существует машины Тьюринга T с алфавитом A и алфавит C, являющийся надалфавитом AÈD такие, что алгоритмы Â_T,C и Á вполне эквивалентны относительно D.

Многоленточная МТ

Простым обобщением МТ является k-ленточная МТ. Вместо одной ленты здесь имеется k лент, каждая из которых обслуживается своей головкой. Имеется управляющее устройство, которое и характеризуется определенным состоянием (в случае одноленточной МТ головка и это устройство объединялись в одном объекте). Конфигурация в этом случае состоит из записей на лентах с указанием мест головок и состояния управляющего устройства. Вместо пары конфигурации мы имеем (k+1)-ку из символа текущего состояния и символов в обозреваемых ячейках.

Команды задаются уже отображением S´A^k®S´{A´{L, R, St}}^k.

В течение одного такта работы можно изменить состояние, напечатать в обозреваемых ячейках новые символы, если это требуется программой и сдвинуть независимо друг от друга какие-нибудь или все головки в тех направлениях, которые предусмотрены командой.

Недетерминированная МТ

Это совершенно иное обобщение понятия МТ. Рассмотрим случай одноленточной недетерминированной машины Тьюринга (НМТ).

Имеется две управляющие головки (УГ) и одна лента. Одна головка Г1 - обычная, такая же, как в МТ, а вторая Г2, которая часто называется угадывающей, может только записывать. Запись на ленте представляет собой слово (условие задачи), записанное слева направо, начиная с ячейки с номером 1. В начальный момент времени обычная головка наблюдает ячейку с номером 1, а пишущая головка - ячейку с номером (-1). Вначале работает только пишущая (угадывающая) головка. На каждом такте работы она может написать символ в наблюдаемой ячейке и сдвинуться влево, либо остановиться. В последнем случае начинает работать обычная головка с состояния q₀. С этого момента НМТ работает точно так же, как МТ с той лишь разницей, что наблюдает не самый крайний слева символ входного слова.

Управляющее устройство пишущей головки принимает решение совершенно произвольно, поэтому может никогда не остановиться.

Ниже в разного рода определениях важна только возможность написания некоторого слова угадывающей головкой. Так как она пишет произвольно, то может написать любую букву в ячейке с номером -1, любую – в ячейке -2 и т.д. Если мы будем рассматривать все возможные результаты работы угадывающей головки, то это будут все возможные слова в данном алфавите.

Далее мы будем различать входное слово I и слово U, записанное угадывающей головкой.

Разница между МТ и НМТ может быть проиллюстрирована с помощью сравнения модели обычных вычислений и моделью параллельных вычислений.

В качестве примеров можно рассмотреть задачи о выполнимости, о гамильтоновом цикле и о простоте числа.

Оракульная МТ

Как и в предыдущем случае здесь две головки (обычная и оракульная), но и две ленты (обычная и оракульная). Во множестве состояний выделены два особых: состояние вопроса к оракулу q_c и резюмирующее состояние q_r. Обе головки управляются одним управляющим устройством. В начальный момент времени на обычной ленте записано входное слово I, начиная с ячейки с номером 1. Все остальные ячейки обеих лент пусты.

Работа оракульной машины Тьюринга (ОМТ) почти аналогична работе двухленточной МТ. Разница в следующем. Если управляющее устройство оказывается в состоянии q_c, то поведение на следующем шаге зависит от фиксированной оракульной функции g:A*®A*.

Этот шаг не изменяет положение основной головки и запись на основной ленте. Его результатом является переход в состояние q_r и изменение за один шаг всего содержимого оракульной ленты по следующему правилу.

Пусть y - слово, записанное на оракульной ленте, начиная с первой ячейки и до ячейки, над которой находится головка. Если головка находится левее ячейки с номером один, то полагается, что y - некоторая заранее оговоренная постоянная. За данный такт на оракульной головке записывается слово g(y), начиная с первой ячейки. Остальная часть ленты стирается, а головка обозревает ее первую ячейку.

То есть мы имеем как бы комбинацию обычной машины Тьюринга М и некоторого оракула g. Вообще говоря, для одной и той же задачи могут быть использованы разные оракулы. Поэтому можно искусственно вычленить ту часть программы ОМТ, которая касается работы обычной головки. Она ведь не касается действий оракульной головки. Именно эту часть программы называют программой ОМТ. Обозначим ее через M. В случае же рассмотрения конкретного оракула g всю программу целиком будем обозначать через M_g, и называть релятивизированной программой ОМТ.

Кодировки входных данных.

Вначале поговорим о длине входа (условия) задачи. Дело в том, что кодировать условия задачи можно разными способами. Поясним это на примерах.

Пример 1. Задача: Требуется найти количество единиц в двоичной записи целого числа.

Если число n задается в виде n+1 единицы *1...1*, то длина входа n+3. Если число задается в десятичной форме, это уже lgn. К этим двум способам добавим двоичную запись числа n. Ее длина log₂n.

Но рассмотрим еще один подход к решению задачи. Пусть у нас есть 2ⁿ перенумерованных ячеек, в каждой из которых содержится число, равное количеству единиц в двоичной записи номера ячейки. Тогда длина входа задачи для числа n равна 2ⁿ log₂n.

Пример 2. Задача о простоте числа.

Если число n задается в виде n+1 единицы *1...1*, то длина входа n+3. Если число задается в десятичной форме, это уже lgn. Если n задано в мультипликативной форме n=p₁^a1…p_k^ak (числа p_i– простые, а сама мультипликативная форма задает разложение числа на простые множители), то длина входа равна S(lgp_i+lga_i), где суммирование ведется от 1 до k.

Пример 3. Задачи на графах.

Выше было много примеров задач на графах. Граф с n вершинами и m ребрами можно задать списками ребер и вершин. В этом случае длина входа лежит между 4n+10m и 4n+10m+(n+2m)[lgn]. Если граф задается списками соседей его вершин, то длина входа лежит между 2n+8m и 2n+8m+2m[lgn]. Порядок же матрицы инциденций графа равен n²-n+1.

Так как понятие входа (условия) задачи не может быть формализовано хотя бы потому, что не формализовано само понятие задачи, то здесь мы вновь вынуждены уповать на наши интуитивные представления.

Это и иллюстрирует первый из приведенных выше примеров. Описанные там два подхода к заданию входа фактически относятся к разным задачам. То есть, понимание условия задачи на интуитивном уровне дает возможность предлагать "разумную" кодировку в том смысле, что разумность заключается в соответствии кодировки условиям задачи.

Первый пример иллюстрирует и важность еще одной меры сложности задачи - объем требуемой при решении памяти. При первом подходе к кодировке входа в данном примере объем памяти в константу раз отличается от длины входа и представляет собой линейную или логарифмическую функцию от n. Время решения задачи, например, ее сложность в худшем (см. ниже) на МТ такая же. Во втором случае решение просто сводится к чтению ответа (на МТ это один такт работы), объем же памяти экспоненциально зависит от n.

Пусть мы теперь имеем "разумные" кодировки. На этом уровне принимается интуитивная гипотеза о некоторой эквивалентности всех возможных "разумных" кодировок входных данных одной и той же массовой задачи.

Второй пример показывает варианты длины кодировок в зависимости от способа задания чисел. Варианты длины кодировок в третьем примере зависят уже от структуры входных данных. Но в обоих случаях можно говорить о, так называемой, полиномиальной эквивалентности.

В дальнейшем нам полезно будет понятие полиномиальной эквивалентности двух функций. Две неотрицательные функции S(n) и R(n) полиномиально эквивалентны, если существуют два полинома Q(x) и P(x) такие, что для всех n справедливы неравенства S(n)£P(R(n)) и R(n)£Q(S(n)).

Пусть S и R две "разумные" схемы кодирования задачи массовой Z. Длины входа в этих схемах для задачи I обозначим через S(I) и R(I). К ним можно применить определение полиномиальной эквивалентности.

В третьем примере все три схемы полиномиально эквивалентны, а во втором полиномиально эквивалентны две последние.

О мерах сложности

Сегодня понятие алгоритма ассоциируется в первую очередь с программой на некотором языке программирования. С точки зрения тезиса Черча, это достаточно естественно.

Однако нас будет интересовать не только проблема эквивалентности различных типов алгоритмов, но также возможность их сравнения и те свойства моделей алгоритмов, которые позволяют оценивать сложность.

Здесь есть определенное противоречие. Проще оценивать сложность алгоритма в рамках достаточно замысловатой модели, например, современного языка программирования. В то же время хотелось бы понимать, насколько подобная модель сравнима, например, с машиной Тьюринга. И не только в смысле эквивалентности, но и при пересчете оценок сложности алгоритма в рамках различных моделей вычисления. Это вопрос очень сложный. Поэтому здесь мы его лишь вскользь коснемся и приведем несколько примеров. В дальнейшем мы периодически будем к нему возвращаться.

В случае решения индивидуальной задачи на машине Тьюринга естественно оценивать сложность алгоритма числом тактов работы МТ. Для НАМ такой мерой может быть количество выполненных в процессе работы преобразований.

В случае НМТ сложность определяется следующим образом. Для одного и того же слова I может существовать множество различных отгадок {U}. На каждой из них обычная головка работает t_T(I,U) тактов. В качестве времени решения задачи на входе I рассматривается

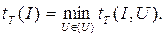
Обратим внимание на то, что понятие «отгадка», с одной стороны, имеет «оракульный подтекст», а с другой – связано с примитивным полным перебором. Пусть существует конечная запись U', обозначающая объект, соответствующий ответу «да». Например, перечень вершин гамильтонова цикла или обход коммивояжера нужного веса. Так как угадывающая головка случайным образом пишет все возможные слова, то один из вариантов ее работы – упомянутая запись. Но в приведенной выше формуле минимум берется по всем возможным записям, поэтому и U’ будет учтена. Дальше работает обычная головка, которая читает отгадку и проверяет. Отгадки, конечно, могут иметь разную длину, поэтому суммарное время чтения и проверки для них может быть разное. Формула даст минимум по этим временам. Пусть он достигается на слове-отгадке V. Так как поиск этого минимума нам ничего с вычислительной точки зрения не стоит, то, можно считать, слово V сразу пишется угадывающей головкой. В этом заключается «оракульность» отгадки. Но оракульность эта достигается бесплатностью перебора по всем возможным записям случайно работающей угадывающей головки. В этом заключается переборный характер механизма получения отгадки.

Для ОМТ сложность решения задачи на входе I определяется совершенно так же, как и для МТ. (Только вычисления-то эти очень разные!)

Кроме временных характеристик рассматриваются и пространственные. В случае МТ сложность задачи может характеризоваться количеством ячеек ленты, которые просматривались головкой в процессе работы.

Говоря о сложности вычисления РАМ, РАСП или упрощенного АЛГОЛа временную сложность индивидуальной задачи оценивают с помощью количества выполненных в процессе решения команд. Но здесь выделяются два подхода.

Если каждая команда требует единицы времени, а каждый регистр занимает единицу памяти, то говорят о моделях вычисления с равномерным весом.

Модель вычисления с логарифмическим весом предполагает, что представление целого числа n в регистре требует ëlog|n|û+1 битов. При этом емкость регистров не ограничена. Время, затраченное на выполнение команды пропорционально длине ее операндов.

Сложность решения массовой задачи можно определять разными способами, исходя их сложности решения индивидуальных задач.

Ниже через Т обозначим некоторую модель вычисления (НАМ, МТ, РАМ и т.п.).

Пусть |Z(n)| - число индивидуальных задач I массовой задачи Z, длина входа которых не превосходит n.

Обозначим время работы алгоритма T (модели вычислений T) на входе I через t_T(I). В случае решения массовой задачи в качестве меры сложности рассматривается функция t_T(n) от длины |I| входа задачи I. Наиболее распространены две меры сложности: "в худшем" и "в среднем". В первом случае

А во втором

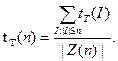
Максимум и сумма берутся по всем индивидуальным задачам I таким, что |I|£n.

Будем различать сложность задачи T_Z и сложность алгоритма A(Z) решения этой задачи T_A(Z). Если фиксирован алгоритм решения задачи A(Z), то по его описанию любой пользователь имеет возможность подробно (пошагово) увидеть, как он работает. Если в качестве сложности алгоритма выбрана некоторая характеристика его работы, например, одна из приведенных выше мер, то используя описание алгоритма, это меру можно вычислить.

Итак, под сложностью алгоритма понимается значение некоторой функции от длины входа. В то же время сложность задачи, как функция от длины входа – это отдельное понятие. Здесь может быть несколько подходов.

Если сложность задачи напрямую определяется сложностью алгоритмов ее решения, то в большинстве случаев удается говорить лишь об оценках этой сложности. Задачу можно решать несколькими алгоритмами, поэтому полагают, что

T_Z ≤ T_A(Z).

Верхней оценкой сложности является наименьшая из известных на данный момент сложность алгоритма ее решения. Если, T_A(Z) - полиномиально ограниченная функция, то говорят, что алгоритм A(Z) (задача Z) имеет полиномиальную сложность, а если экспоненциально ограниченная – то экспоненциальную сложность. В следующем разделе мы в качестве примеров такого подхода рассмотрим несколько известных вам задач.

Если бы была известна некоторая нижняя оценка сложности

F(n)≤ T_Z,

совпадающая с верхней, то, то сложность задачи была бы определена, а исследователи бы знали, что существующий на данный момент алгоритм ее решения является наилучшим из возможных и дальнейшие попытки поиска более быстрого алгоритма будут безуспешными. Но такая ситуация имеется лишь в очень малом количестве сравнительно простых задач, таких как приведенные ниже: задача нахождения минимального числа (здесь сложность равна O(n)) или задача сортировки (здесь сложность равна O(nlogn)).

Дело в том, что нижняя оценка сложности получается из анализа структуры задачи, а не из методов ее решения. На сегодня типичной является ситуация, когда нижняя оценка – экспонента, нижняя – линейная функция. Экспоненциальные нижние оценки сложности для некоторых задач были впервые получены в 1980-х годах.

Другой подход к анализу сложности связан с понятием схемы из функциональных элементов.

Теоремы сравнения

Подведем теперь некоторый итог нашему рассмотрению. Для этого мы сформулируем и обсудим несколько утверждений. Подробные доказательства можно найти в [3] и в [1].

Интуитивно очевидно, что сводить сравнительно бедный (простой) формализм к более богатому (сложному) тяжелее, чем наоборот. С другой стороны, оценивать сложность решения той или иной задачи с помощью программы на современном языке программирования проще, чем сложность ее решения на МТ. В то же время многие теоретические результаты сформулированы для такой модели, как МТ. Утверждения данного раздела и позволяют проверить, насколько такие оценки теоретически обоснованы.

Первые два утверждения касаются НАМ и МТ.

Теорема. Пусть T - машина Тьюринга с алфавитом A и С - надалфавит А. Тогда существует нормальный алгорифм Маркова Á над С, вполне эквивалентный алгоритму Тьюринга Â_T,C.

Справедливо и обратное утверждение.

Теорема. Пусть Á - нормальный алгорифм Маркова в алфавите A, D,dÏA. C={D,d}ÈA. Тогда существует машина Тьюринга T такая, что алгоритм Тьюринга Â_T,C в алфавите C обладает следующим свойством. Для любого слова P в алфавите A Â_T,C применим в том и только в том случае, когда к этому слову применим Á, а результатом работы Â_T,C является слово Á(P), окруженное конечными последовательностями из D.

Займемся теперь сравнение РАМ и РАСП.

Теорема. Как при равномерном, так и при логарифмическом весе для любой РАМ-программы с временной сложностью T(n) найдется эквивалентная ей РАСП программа с временной сложностью, не превосходящей kT(n), k - некоторая постоянная.

Теорема. Как при равномерном, так и при логарифмическом весе для любой РАСП-программы с временной сложностью T(n) найдется эквивалентная ей РАМ программа с временной сложностью, не превосходящей kT(n), k - некоторая постоянная.

Эти утверждения позволяют использовать в рассуждениях ту из моделей, которая в данном случае более удобна.

Рассмотрим теперь связь РАМ и МТ.

Возьмем задачу в форме распознавания Z и соответствующий ей язык L_Z. Все перечисленные формальные схемы алгоритма позволяют ввести понятие допустимости языка алгоритмом.

Например, МТ допускает язык L_Z тогда, когда она останавливается в специально отведенном для этого конечном состоянии q_y только на словах этого языка, являющихся условиями индивидуальных задач с ответом "да".

Конечно, вместо состояния можно требовать написания какого-то символа на ленте. Так в РАМ, РАСП и упрощенном АЛГОЛе говорят, что программа допускает язык L_Z тогда, когда она останавливается, записав на выходной ленте 1 только на словах этого языка, являющихся условиями индивидуальных задач с ответом "да".

Заметим, что на всех остальных словах программа либо вообще не останавливается (зацикливается), либо останавливается с некоторой другой записью на ленте.

Теорема. Пусть L - язык, допускаемый некоторой РАМ за время T(n) при логарифмическом весе. Если в программе РАМ нем умножений и делений, то существует многоленточная МТ, допускающая этот язык за время O(T²(n)).

Аналогичное утверждение для равномерного веса неверно.

Действительно, в случае МТ равномерного веса быть не может. В ячейке записан один символ. Его расшифровка внутри программы просто должна развернуть всю запись числа. А как это делается: явным образом с занятием новых ячеек или неявно в виде последовательности выполняемых команд, - это уже не важно.

Для РАМ же логарифмический вес является абстрактным упрощением, которое иногда полезно, если применяется осознанно.

Сказанное поясняет пример умножения n чисел вида .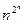

РАМ это может сделать за O(n) шагов при равномерном весе. Ведь в регистр помещается число любого размера. В то время как на МТ только вклад тактов, на которых осуществляется считывание входного слова, составит более 2ⁿ. То есть даже полиномиальной эквивалентности между сложностями вычислений в этих моделях.

Задача сортировки.

В дискретной математике сортировке подлежат объекты разной природы. Пусть необходимо отсортировать (например, по возрастанию) числовой массив из n элементов. Без ограничения общности будем считать, что – степень двойки (чтобы не возиться с целыми частями). В качестве элементарной операции используется операция сравнения чисел. Чтобы сравнивать числа нужно их различать как объекты сортировки (эти объекты имеют численные значения). Сравнение – это операция с результатом «да» или «нет», поэтому кодируем объекты сортировки бинарными последовательностями. Какова минимальная длина такой последовательности для множества их M элементов? Очевидно, что это  log M. В теории информации этот факт известен как энтропия по Хартли.

Если мы упорядочиваем  n  объектов (чисел), то в зависимости от их значений можно получить n! различных упорядочиваний. Последовательность сравнений для их различения не может быть меньше log(n!). Применяем формулу Стирлинга: log(n!)=(n+1/2)logn-n+0,5log2π+α/(12n), 0< α <1, n→∞ . Отсюда следует, что задачу сортировки нельзя решить со сложностью алгоритма, меньшей  O(nlogn).

C 1950-х годов разработано много методов сортировки со сложностью алгоритма, равной O(nlogn).

Задача о камнях.

Здесь тоже дан массив из n чисел, но его не нужно упорядочивать или искать в нем число. Нужно попробовать разложить его на две «максимально» равные части. Каждая из этих частей является подмножеством всего множества камней и полностью определяет другую (оставшиеся камни). Всего подмножеств, как вы знаете, 2ⁿ. На сегодняшний день не существует алгоритма решения этой задачи, отличного от полного перебора. Перебирая последовательно все подмножества мы сравниваем их вес с числом (S a_i)/2). Если получили совпадение, то ответ «да», если же такого совпадения мы не получаем после того, как все множества просмотрены, то ответ «нет». Сложность такого алгоритма O(n2ⁿ).

Простота числа.

Пусть дано натуральное N. Тогда длина входа задачи: n=logN.

Из школы известно два алгоритма: простой перебор и решето Эратосфена.

В первом случае нужно осуществить n^1/2 делений. Сложность алгоритма t(n)=2^n/2.

Можно показать, что сложность алгоритма решето Эратосфена составляет O(2ⁿlog n) операций в модели вычислений RAM, или O(2ⁿ n(log n)) битовых операций, при условии вычисления и зачеркивания каждого кратного числа за время O(1). Таким образом, другая из приведенных в качестве примеров задач – задача о разложении числа на множители – тоже имеет экспоненциальную сложность, так как задача о простоте – это частный случай.

Задача коммивояжера.

Число гамильтоновых циклов в графе G=(V,E), |V|=n, |E|=m, с матрицей весов ребер  C=(c_ij),  равно (n-1)!. Сумму весов ребер одного гамильтонова цикла можно найти за O(n). Общая трудоемкость алгоритма O(n!)  = O((n/e)^n+1/2). Так может быть здесь, как и в предыдущем случае, можно ее сократить до простого полинома? Оказывается нельзя. На сегодня не существует полиномиальных алгоритмов решения задачи коммивояжера, лучшие алгоритмы имеют экспоненциальную трудоемкость «в худшем случае».

В таких случаях на практике вместо точного решения пытаются найти приближенное или используют методы «направленного перебора» (методы ветвей и границ), но об этом мы поговорим позже.

Задача о кратчайшем пути.

В графе G=(V,E), |V|=n, |E|=m, с матрицей весов ребер  C=(c_ij) для двух фиксированных вершин ищется путь наименьшей длины между ними. (Длина пути – сумма весов входящих в него ребер). Если мы будем искать его методом полного перебора, то снова получим экспоненциальную оценку. И ничего с ней поделать нельзя, если веса ребер – произвольные числа. А если они неотрицательны, то можно избежать переборного алгоритма и построить более эффективный Алгоритм Дейкстры.

Сложность алгоритма Дейкстры зависит от способа нахождения вершины v, а также способа хранения множества непосещенных вершин и способа обновления меток. Обозначим через n количество вершин, а через m — количество ребер в графе G.

В простейшем случае, когда для поиска вершины с минимальной пометкой просматривается все множество вершин  время работы алгоритма есть O(n² + m).  Для разреженных графов (то есть таких, для которых m много меньше n²) скорость работы возможной реализации O(nlog n + mlog n).

Оценки сложности СФЭ.

Оценки функции Шеннона L(n) строятся из тех же соображений, что и оценки сложности задачи. Верхние оценки получаются путем построения конкретной СФЭ, реализующей функцию f(n). Для этого было разработано в 1950-е годя целое направление в дискретной математике – методы синтеза СФЭ. А вот нижние оценки получаются «из мощностных соображений».

Построим СФЭ, реализующую функцию f = 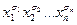. Перегруппируем множители, собрав в одном месте переменные с нулевыми степенями. Тогда, перенумеровав переменные, функцию можно переписать в виде

f = (x_i & . .. & x_k)& 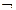(х_к+1 Vх_к+2 V ...V х_п).

Заметим, что в этой формуле не более n операций. Значит, сложность схемы данной функции не превосходит n. Отсюда следует очевидный метод построения СФЭ по совершенной ДНФ функции. С его помощью строится СФЭ сложности не более (n +1) 2ⁿ.

Утв. L(n) ≤(n +1) 2ⁿ.    

Замечание. На самом деле легко доказать, что L(n)≤ (n + 1) 2^n-1. Действительно, посмотрим на таблицу значений нашей функции и выясним, чего в ней больше: нулей или единиц. В зависимости от этого будем исполь­зовать, соответственно, СДНФ либо СКНФ. В самом худшем случае будет 2^n-1 дизъюнкций или коньюнкций.

Дальнейшее улучшение позволяет избавиться и от множителя n. Построим по индукции СФЭ, которая будет реализовывать множество функций K_n – множество всех конъюнкции 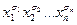 - со сложностью C(n), которая асимптотически равна 2ⁿ⁺¹.

Обозначим через K_n множество всех функций вида 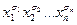. Сейчас мы будем строить схему, которая реализует все функции из K_n. Сложность такой схемы обозначим C(n). При n = 1 получается схема без элементов. Предположим, что мы уже построили схему для всех множеств с номерами меньше n. Зафиксируем число k < n. Построим схему, реализующую все функции из K_n, используя в качестве подсхем две схемы: для K_k и для K_n-k. Тогда первые k сомножителей реализуются конъюнктором K_k, а остальные n-k – конъюнктором K_n-k.

Возьмём по одному выходу из схем для K_k и K_n-k, реализующие их, и подключим их к конъюнктору. Получим схему, реализующую одну конъюнкцию от n переменных. Также поступим со всеми 2ⁿ конъюнкциями от n переменных, то есть будем строить их, используя соответствующие выходы в схемах K_k и K_n-k, связывая их конъюнктором. Итого получим схему для K_n, затратив C(k)+C(n — k)+2ⁿ элементов. Теперь возьмём k := n/2 и получим С(п) ≤2ⁿ +2С( n/2) = 2ⁿ(2^n/2+2С( n/4))=2ⁿ+2^n/2+1+4С( n/4)) . Отсюда следует, что можно (асимптотически) улучшить оценку для L(n): реализовав все конъюнкции ценой ~ 2ⁿ элементов, склеим их не более чем 2ⁿ дизъюнкциями, в итоге получим схему сложности порядка 2ⁿ⁺¹.

Дальнейшее улучшение в n раз дает метод Шеннона синтеза схем. Он просто использует разложение функции по k переменным

F(x₁,…,x_n) = .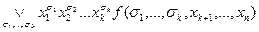

Пусть k = n-q. Реализуем все конъюнкции K_k первых k переменных, при этом потратим 2^k элементов. Кроме этого, может потребоваться реализовать все функции от q переменных, которых всего 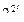. Каждую из них можно реализовать со сложностью q2^q. При склейке основной схемы по указанной выше формуле потребуется ещё 2^k конъюнкторов (для вычисления слагаемых) и ещё 2^k -1 дизъюнкторов. Итого

L(n) < 2^k + 2^k + (2^k — 1) + q 2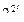^q  < 3 • 2^k + q 2^q .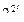     

Положим q := [logn] — 1. Тогда

L(n) < 6•2^n-[logn] + n•logn•2^n/2-1 =12•2ⁿ / n + n•logn•2^n/2-1 < 12•2ⁿ / n .

Наконец, следующая теорема О.Б.Лупанова дает окончательную неулучшаемую асимптотическую оценку.

Теорема. Справедливо соотношение L(n) < 2ⁿ / n .

Доказательство. Рассмотрим произвольную булеву функцию n переменных. Отделим q := n-k первых переменных и рассмотрим таблицу, в которой 2^k строк и 2^q столбцов. Строки занумеруем всевозможными значениями послед­них k переменных, а столбцы — всевозможными значениями первых q переменных. Ячейки таблицы заполним значениями функции. Каждый столбец представляет собой значения функции, полученной подстановкой кон­стант в первые q переменных, то есть . Разрежем таблицу на горизонтальные полоски по s строк в каждой (последняя полоса будет, возможно, меньше; пусть в ней s' < s строк). Число полос будет равно p=[2^k /s]< 2^k /s+1.

Через I_i обозначим индикатор i-й полосы, то есть функцию, которая равна единице на строках этой полосы, и только на них. Обозначим теперь

 

Такие функции называются обрезанными функциями. Ясно, что

= .

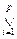
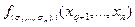Тогда имеем

.

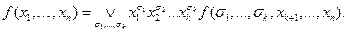Реализуем все конъюнкции первых q переменных, потратив 2^q элементов. Кроме этого, реализуем все конъюнк­ции последних k переменных, потратив 2^k элементов. Все обрезанные функции имеют не более s ненулевых значений, значит, их количество не превышает 2^s. Поскольку все конъюнкции последних переменных уже есть, на изготовление СДНФ для каждой обрезанной функции уйдёт всего s дизъюнкций, значит, всего на реализацию обрезанных функций каждой полосы мы потратим не более s2^s элементов, а всего — не более ps 2^s.

На сборку каждой уйдёт ещё p дизъюнкций (поэтому всего на это уйдёт p 2^q операций), а на сборку функции f уйдёт ещё 2^q конъюнкций и 2^q дизъюнкций.

Суммируя полученные оценки, имеем

L( f) < 2^q + 2^k + ps2^s + p2^q + 2^q + 2^q = 3 2^q + ps 2^s + p2^q + 2^k.     

Вспоминая, что р< 2^k /s+1, получаем

L( f) < 3 • 2 ^q +(2^k /s+ 1)(s2^s + 2^q) + 2^k.    

Видно, что s должно быть порядка п, но всё же чуть меньше его. Что касается к, то нужно, чтобы 2^k /s→∞, чтобы нам не мешала единица в скобках. Положим k := [2 log n] и s := [n — 4 log n]. Подставляя эти значения, получаем оценку порядка 2ⁿ / n.

Теорема доказана.

Чтобы доказать, что получена асимптотически неулучшаемая оценка, нужно аналогичную асимптотику L(n) 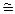> 2ⁿ / n снизу.

Пусть P* (n) — функции, существенно зависящие от n переменных. N(h, n) — число функций, существенно зависящих от n переменных, которые реализуются схемами слож­ности, не превосходящей h. N^'(h, n) — число функций, существенно зависящих от n переменных, которые реализуются схемами слож­ности ровно h; N^''(h, n) — число схем сложности h для функций, существенно зависящих от n переменных. Очевидно, что N^' = N, потому что всегда можно дополнить схему ничего не делающими элементами. Оче­видно также, что N≤N^'', так как одну функцию можно реализовать разными схемами, но не наоборот.

Покажем, что для любого ε>0, число функций, реализуемых схемами сложностью меньше (1-ε ) 2ⁿ /n, гораздо меньше, чем всех функций. Итак, покажем, что для h_o= (1-ε ) 2ⁿ / n выполнено соотношение N( h_o, n)<< |P*(n)|. Мы будем оценивать величину N, мажорируя её величиной N''.

Пусть y(p, q) — число графов с q ребрами и p= h + n вершинами (n входов и h элементов), N''(h, n, q) — число схем с q ребрами. Сколько схем можно сделать из одного графа? У нас имеется не более:

· 2^q способов выбрать ориентацию ребер;

· ( h + n) ⁿ способов выбрать входы;

· 3^h способов присвоения вершинам различных ФЭ;

· h + n способов выбора выхода.

Число γ(n,m) связных графов с n вершинами и m ребрами не превосходит  n^m-nconst^n+m. Действительно, чтобы из n-вершинного дерева сделать m-рёберный граф, нужно дополнительно провести ещё m—(n— 1)= k ребро. Из каждой вершины дерева можно выпустить куда-то ребро (так, чтобы второй конец пока не входил ни в какую вершину). Это можно сделать, очевидно, 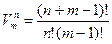 способами. Теперь эти концы надо как-то подсоединить к имеющимся вершинам. Это можно сделать mⁿ способами. Значит, существует не более

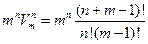 способов получить из дерева граф. А поскольку количество деревьев не превосходит 4^n-1, то в итоге имеем оценку сверху

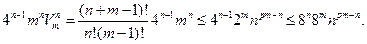Таким образом, достаточно взять const = 8.

Отсюда получаем:

N(h, n, q) ≤ γ(n,m) 2^q (h + n)ⁿ+¹ 3^h ≤ const^h+ⁿ+^q(h + n)^q—h+¹ 2^q 3^h. (15)

Вспоминая, что q ≤ 2h, и собирая константы в новую константуB , имеем:

N''(h, n, q)≤ B^3h+ⁿ(h + n)^h+¹.   

Теперь получим оценку для N^''(n, h):

N''(h, n, q)≤ B^3h+ⁿ(h + n)^h+¹.

 Нам нужно убедиться, что N''(h_o,n) < |P*(n)| при достаточно больших n. Заметим, что

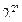|P*(n)| >  — n 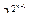≈ 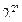.  Таким образом, требуемое неравенство будет выполнено, если при n→∞ будет выполняться

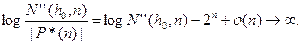
Далее для достаточно боль­ших n:

log N’’(h_o,n) — 2ⁿ + o(1) ≤ (h_o + n) log(C(h_o + n)) — 2ⁿ + o(1)≤((1-ε)2ⁿ/n+n)n

-2ⁿ + o(l) = (1-ε)2ⁿ + n² - 2ⁿ + o(l) = n² + o(1) — ε2ⁿ →∞ при n→∞.

Что и требовалось доказать.

 

Теорема. Справедливо соотношение L(n) 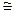2ⁿ / n .

Теория NP-полноты

В конце 60-х и начале 70-х годов был внесен интересный вклад в теорию сложности, касающийся сравнения различных типов алгоритмов. Главная роль здесь принадлежит американскому математику С.А.Куку.

Три фундаментальных части предложенной Куком концепции заключаются в следующем.

1. Были введены определения двух классов задач. Один из них был связан с полиномиальными алгоритмами, а другой - с переборными.

2. Были введены понятия сводимости задач. Сводимость позволяла характеризовать принадлежность к определенному классу.

3. Для некоторой конкретной задачи было конструктивно доказано, что она в определенном смысле может рассматриваться, как самая сложная. (С помощью сводимости затем множество таких самых сложных задач было дополнено.)

Классы P и NP.

Рассмотрим дискретную оптимизационную задачу Z в форме распознавания. Ей, как было выше описано, сопоставляется язык L_Z.

Класс P - это класс языков, допускаемых МТ за полиномиальное время. (То есть эта МТ, во-первых, допускает язык, а, во-вторых, время ее работы ограничено полиномом.)

Задачи (языки) из этого класса называют полиномиально разрешимыми.

В случае НМТ для одного и того же слова I, представляющего собой запись условия некоторой индивидуальной задачи, может существовать множество различных отгадок {U}. Зафиксируем слово I и рассмотрим все возможные вычисления НМТ на различных отгадках. На каждой из них обычная головка работает t_T(I,U) тактов.

Если хотя бы для одного такого вычисления НМТ за конечное число шагов остановится в конечном состоянии q_y ,то это вычисление называется принимающим, t_T(I,U) полагается равным числу тактов работы НМТ. В противном случае (НМТ зацикливается или останавливается в состоянии q_n) вычисление называется непринимающим.

В качестве меры трудоемкости решения задачи I в форме распознавания на НМТ рассматривается величина

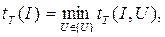
где минимум берется по всем принимающим вычислениям.

Если для некоторой массовой задачи Z НМТ допускает ее индивидуальную задачу I тогда и только тогда, когда I имеет ответ "да", то говорят, что НМТ допускает язык L_Z .

Класс NP - это класс языков, допускаемых НМТ за полиномиальное время. (То есть эта НМТ, во-первых, допускает язык, а, во-вторых, время ее работы ограничено полиномом.)

Теорема. Если ZÎNP, то существует такой полином p, что Z может быть решена на детерминированной МТ за время O(2^p(n)).

Доказательство. Пусть T - НМТ, решающая Z за время q(n). То есть для каждого I найдется отгадка U(I) такая, что после ее записи НМТ работает уже как обычная МТ, а число тактов работы не превосходит q(n). Ясно, что число символов самой отгадки (ее нужно прочесть в процессе решения) не может превосходить q(n).

Пусть k - число символов в алфавите НМТ. Тогда всего нужно рассмотреть k^q(n) отгадок. Построим такую МТ, которая работает также, как обычная головка нашей НМТ, а на входной ленте у нее записаны все k^q(n) отгадок. Она поочередно просматривает отгадки. Если хотя бы на одной она останавливается в состоянии, то вычисление завершается. Временная сложность не превосходит q(n)k^q(n), что при надлежащем выборе полинома не превосходит O(2^p(n)).

Теорема доказана.

Сводимость задач

Смысл сводимости

Мы уже видели, что существует определенный качественный разрыв между алгоритмами полиномиальной и экспоненциальной сложности. Но сложность алгоритма решения задачи еще не полностью характеризует сложность решения задачи. Действительно, для одной и той же задачи могут быть построены алгоритмы решения разной сложности. С эти связана одна из самых важных проблем теории сложности - получение "хороших" нижних оценок сложности задачи.

Если для некоторой задачи Z построен алгоритм сложности O(f(n)), то можно говорить, что сложность решения задачи не превосходит O(f(n)). Таким образом, верхние оценки сложности решения задачи могут быть получены конструктивным образом с помощью построения конкретных алгоритмов. Нижние оценки - это утверждения следующего типа: "Задача Z не может быть решена никаким алгоритмом со сложностью, меньшей O(g(n))". Эти оценки нельзя получить, построив конкретный алгоритм. (Может быть, это просто плохой алгоритм, а в будущем кто-то построит хороший.) Эти оценки строятся путем анализа свойств задачи, возможностей кодировок условия и пр. Тривиальная нижняя оценка - длина входа задачи. Но выше мы видели, что проблемы кодировки входа достаточно тонкие. Хотя в большинстве случаев здесь можно все прояснить.

Лишь для небольшого количества задач верхние и нижние оценки сложности близки. Например, сложность сортировки n чисел равна O(nlogn). То есть, известен конкретный алгоритм, который с такой сложностью сортирует n чисел. Кроме того, доказано, что эту задачу нельзя решить быстрее, чем за O(nlogn) шагов.

Для многих полиномиальных задач верхняя и нижняя оценки различаются степенью полинома. Это может быть достаточно существенное различие, но в силу сказанного выше оно все же не столь критично как различие экспоненциальной верхней оценки, например, от линейной нижней. А это, к сожалению, достаточно типичная ситуация для многих задач дискретной оптимизации.

Но кроме разделения задач на два класса: с полиномиальной и экспоненциальной верхней оценкой сложности,- хотелось бы, в свою очередь, более детально разобраться со вторым классом.

Вот для этого и служит понятие сводимости. Это, грубо говоря, установление некоторой связи между парой задач. Смысл этой связи иллюстрирует следующий пример. Пусть известно две задачи X и Y. Задача X сформулирована 200 лет назад и с тех пор ничего лучшего, чем экспоненциальный алгоритм для нее не построено. Задача Y сформулирована вчера, и мы хотим приложить максимум усилий для ее эффективного решения. Под таким решением мы подразумеваем полиномиальный алгоритм.

Предположим теперь, что существует некоторое понятие сводимости. Если эта сводимость так устанавливается между X и Y, что наличие полиномиального алгоритма для Y влечет за собой существование полиномиального алгоритма для X, то интуитивно ясно, что подобный факт существенно повлияет на наш оптимизм в вопросе эффективного решения задачи Y и, возможно, после здравого рассуждения мы ограничимся эвристиками и переборными алгоритмами для нашей новой задачи.

Было введено несколько определений сводимости.

Полиномиальная сводимость

Рассмотрим класс задач NP. Здесь можно говорить о сводимости языков. Формальное определения полиномиальной сводимости следующее.

Определение. Говорят, что язык L₁ÍA* сводится к языку L₂ÍB*, если существует такое отображение f: A*®B*, что выполняются два условия.

1. Функция f вычисляется за полиномиальное время. (Например, существует МТ, которая за полиномиальное число тактов вычисляет эту функцию.)

2. Для любого входа IÎA* соотношение IÎL₁ выполняется тогда и только тогда, когда выполняется соотношение f(I)ÎL₂.

Сводимость языков обозначается L₁µL₂.

Вначале приведем два простых примера.

Пример. Задача "гамильтонов цикл" сводится к задаче "коммивояжер".

Схема решения. Матрица весов ребер A задачи коммивояжер строится из матрицы инциденций графа G задачи гамильтонов цикл по правилам: наличие ребра в G соответствует единице в A, а его отсутствие соответствует двойке. Число B для задачи коммивояжер определяется равным числу вершин в G.

Определим задачу «3-КНФ» как частный случай задачи «КНФ-выпонимость», в котором каждая КНФ содержит не более трех литералов.

Теперь приведем два очевидных свойства соотношения "сводимость".

Лемма. Если L₁µL₂ и L₂ÎP, то L₂ÎP.

Доказательство. Смысл этого утверждения в том, что сведения некоторой новой задачи к известной полиномиально разрешимой позволяет утверждать, что эта новая также полиномиально разрешима.

Мы приводим доказательство этого утверждения, так как оно конструктивно и, по сути дела, описывает алгоритм решения новой задачи.

Пусть A и B алфавиты языков L₁ и L₂, а функция f: A*®B* осуществляет полиномиальную сводимость L₁ к L₂.

Так как L₂ÎP, то существует МТ, которая за полиномиальное число тактов решает эту задачу. Обозначим эту машину через М₂. Через М_f обозначим машину Тьюринга, которая за полиномиальное число тактов вычисляет эту функцию f. Верхние оценки сложности решения обозначим через p₂(n) и p_f(n), где p₂ и p_f - некоторые полиномы.

Построим теперь МТ, которая решает первую задачу (допускает язык L₁). Пусть задан некоторый вход IÎL₁ (условие индивидуальной задачи). Сначала с помощью М_f преобразуем его во вход f(I) второй задачи. Затем с помощью М₂ выясняем справедливость соотношения f(I)ÎL₂. Так как для любого входа IÎA* соотношение IÎL₁ выполняется тогда и только тогда, когда выполняется соотношение f(I)ÎL₂, то требуемый алгоритм построен. Время работы ограничено O(p₂(p_f(I)) + p_f(I))), что является полиномом, от n.

Лемма доказана.

Мы видим, что в построенном алгоритме по одному разу работают обе машины Тьюринга. В случае программы на некотором современном языке программирования это аналогично ситуации, когда некоторая программа составляется путем последовательного однократного выполнения двух других программ.

Соотношение полиномиальной сводимости транзитивно, то есть справедливо следующее соотношение.

Лемма. Если L₁µL₂ и L₂µL₃, то L₁µL₃.

Доказательство этого утверждения очевидно.

Определение. Задача из NP называется NP-полной, если к ней полиномиально сводится любая задача из NP.

Класс NP-полных задач обозначается через NPC.

Сводимость по Тьюрингу

Это иной подход к понятию сводимости. Заметим, что в оригинальной работе Кука использовался именно он.

Этот тип сводимости касается более широкого класса задач, чем задачи в форме распознавания.

В задачах оптимизации Z для каждого входа I условия задачи определяют множество конечных объектов S_Z(I), которые являются ее решениями. Так, в задаче "гамильтонов цикл" это некоторый гамильтонов цикл, а в задаче "коммивояжер" на минимум - это гамильтонов цикл минимального веса. Первая из этих задач является задачей в форме распознавания, а вторая таковой не является. Но даже при решении первой как задачи в форме распознавания ответом будет только утверждение о наличии или отсутствии гамильтонова цикла, в то время как ее же решение в оптимизационной форме предполагает в качестве ответа предъявление требуемого гамильтонова цикла в случае его наличия.

Считается, что некоторый алгоритм решает задачу Z, если он выдает некоторый sÎS_Z(I), если множество S_Z(I) не пусто. В противном случае он выдает некоторый условленный ответ, например, "нет".

Выше мы видели, что для формальных рассуждений удобно представлять задачу в форме распознавания в виде некоторого языка. По той же причине рассматриваемые здесь задачи удобно представлять в виде известного формального объекта, называемого словарным отношением.

Пусть имеется алфавит A. Обозначим через A⁺ множество всех непустых слов этого алфавита. Словарным отношением над алфавитом A называется бинарное отношение RÍA⁺xA⁺.

Со словарным отношением R свяжем язык L над A. Определим некоторое словарное отношение R={(I,s): IÎA⁺ и IÎL}. Здесь s- любой фиксированный символ алфавита A.

Говорят, что функция f: A*®A*реализует словарное отношение R тогда и только тогда, когда для каждого IÎA⁺ имеет месть f(I)=D, если не существует yÎA⁺ такого, что(I,y)ÎR; в противном случае f(I)=y для некоторого yÎA⁺, (I,y)ÎR.

МТ разрешает отношение R, если она вычисляет функцию f, которая реализует R.

Если раньше речь шла только о кодировании условия задачи Z, то теперь схема кодирования включает как кодирование входа I, так и кодирование решения S_Z(I). Тогда задаче Z можно сопоставить словарное отношение R={(x,y)}, где x - код входа индивидуальной задачи, а y -код некоторого ее решения. (Как и раньше, чтобы не загромождать изложение мы не будем различать сам вход и его код.)

Сводимость по Тьюрингу базируется на определенном выше понятии оракульной МТ.

Определение. Пусть R и R' - два словарных отношения над A. Будем говорить, что R сводится по Тьюрингу к R', если существует оракульная машина Тьюринга M с входным алфавитом A такая, что для любой функции g:A*®A*, реализующей словарное отношение R', релятивизированная программа M_g будет полиномиальной программой ОМТ, а функция, вычисляемая программой M_g, будет реализовывать отношение R.

Обозначим этот тип сводимости как Rµ_TR'. Как и в случае полиномиальной сводимости имеет место транзитивность.

Лемма. Если L₁µ_TL₂ и L₂µ_TL₃, то L₁µ_TL₃.

Данное понятие сводимости относится уже не только к задача в форме распознавания, т.е. оно является более широким и, возможно, позволяет анализировать сложность задач за пределами класса NP задачи.

Определение. Словарное отношение R назовем NP -трудным, если существует NP-полный язык L (представленный как словарное отношение), который сводится по Тьюрингу к R, т.е. Lµ_TR.

Более неформально NP-трудная задача определяется как задача, к которой по Тьюрингу сводится некоторая NP-полная задача.

Пример. Задача "разбиение" сводится по Тьюрингу к задаче "K-е по порядку подмножество".

Первая определена выше. Вторая задача состоит в следующем. Задано конечное множество A, каждый его элемент a имеет размер s(a), выраженный натуральным числом. Заданы также два неотрицательных числа K£2^|A| и

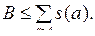
Вопрос заключается в следующем. Существует ли не менее K различных подмножеств A'ÍA, удовлетворяющих условию s(A')£B, где

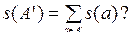
Весьма вероятно, что эта задача не принадлежит классу P. Более того, она может не принадлежать и NP.Интуитивно очевидный путь ее решения на НМТ требует угадывания K подмножеств множества A. Пока неизвестен способ записать эти угаданные подмножества на ленте в виде слова, длина которого была бы полиномом от |A|logKlogs(A). Если говорить о полиномиальной сводимости, то сегодня неизвестно никакой NP-полной задачи, которая бы сводилась к задаче "K-е по порядку подмножество".

Покажем теперь, что задача "разбиение" сводится по Тьюрингу к задаче "K-е по порядку подмножество".

Пусть S(A, s, B, K) - программа для решения задачи "K-е по порядку подмножество". Положим |A|=n. Условие индивидуальной задачи "разбиение" задаются просто в виде множества A с размерами элементов. Программа для решения задачи "разбиение" начинается с вычисления s(A). Если оно нечетно, то ответ "нет". В противном случае полагаем B=s(A)/2 и применяем приведенный ниже алгоритм (он использует процедуру S(A, s, B, K)), позволяющий определить число L* подмножеств A'ÍA, удовлетворяющих условию s(A')£B.

1. Шаг 1. Положить L_min=0, L_max=2ⁿ.

2. Шаг 2. Если L_min-L_max=1, то положить L*= L_min и остановиться.

3. Шаг 3. Положить L=(L_min+L_max)/2 и вызвать подпрограмму S(A, s, B, L). Если ответ "да", то положить L_min=Lи перейти к шагу 2. В противном случае положить L_max=L и перейти к шагу 2.

Подпрограмма S(A, s, B, L) вызывается ровно n раз. Требуется еще один вызов S(A,s,B-1,L*) для определения ответа в задаче "разбиение". Если ответ будет "да", то все подмножества A'ÍA, удовлетворяющих условию s(A')£B, должны удовлетворять и условию s(A')£B-1. Поэтому ответом в задаче "разбиение" будет "нет". В противном случае должно существовать некоторое подмножество A'ÍA, удовлетворяющее условию s(A')=B. Поэтому ответом в задаче "разбиение" будет "да".

Мы видим, что данный тип сводимости, возможно, позволяет выйти за пределы класса NP и оценивать сложность задач, сформулированных не только в виде задач распознавания. Ряд известных оптимизационных задач мы задавали в форме распознавания: задача о коммивояжере, задача ЦЛП, задача о клике и др. В этой форме они принадлежат классу NP и, как мы ниже увидим, являются NP-полными. Их NP-полнота доказывается с использованием полиномиальной сводимости. Если их задавать в традиционной для них оптимизационной форме, то нельзя использовать понятие полиномиальной сводимости. В то же время можно использовать сводимость по Тьюрингу. Ко всем таким задачам можно по Тьюрингу сводить NP-полные задачи. Поэтому оптимизационная форма NP-полной задачи, как правило, является NP-трудной задачей.

 

Теорема Кука

Само понятие NP-полноты - инструмент исключительно описательный. Из приведенных выше утверждений легко получить следующую теорему.

Теорема. Если L₁µL₂ и L₁ является NP-полной задачей, тогда LÎтакже NP-полная задача.

Это утверждение позволяет гипотетически разбить весь класс NP на части. То есть выделить в нем некоторое множество сравнительно простых задач. Это класс P. И множество задач самых сложных –  класс NPC. Это множество NP-полных задач.

Пусть, например, появилась некоторая новая задача Z. Мы пытаемся оценить ее сложность. Если мы придумали полиномиальный алгоритм ее решения, то она относится к классу P. Если наши усилия по построению такого алгоритма долго не увенчиваются успехом, то мы можем попытаться доказать с помощью сформулированной теоремы NP-полноту задачи Z. Если это удается, то можно утверждать, что новая задача в некотором смысле не проще многих известных задач, NP-полнота которых уже доказана.

Но доказательство NP-полноты можно проводить разными способами. Пока нам ясно два: использовать сформулированную только что теорему и технику сведения одной конкретной задачи к другой или непосредственно исходить из определения. Первый способ кажется предпочтительней (да так, наверное, и есть). Но для применения теоремы нужно иметь хотя бы одну NP-полную задачу.

Вот в этом и основной смысл теоремы Кука. Он доказал, пользуясь только определением, NP-полноту одной конкретной задачи. Всюду в дальнейшем пустой символ будем обозначать через L.

Теорема Кука. Задача о выполнимости (ЗВ) NP-полна.

Мы приведем схему доказательства этой теоремы, взятую из лекций А.Разборова.

По определению NP-полноты мы должны доказать два факта.

1. ЗВ лежит в NP.

2. Любая задача Z из NP полиномиально сводится к ЗВ.

Для доказательства первого факта мы должны построить НМТ, которая за полиномиальное время решает ЗВ. Это очевидно. Действительно, вход задачи - КНФ f от p переменных x₁,…,x_p, заданная в виде конъюнкции из m конъюнкций. Если она обращается в единицу на некотором наборе значений переменных x₁=a₁,…,x_p=a_p, то угадывающая головка данный набор длины p напишет. Подстановка в формулу и проверка требует полиномильного по длине входа времени.

Доказательство второго факта строится по следующему принципу. По входу w задачи Z строится вход задачи ЗВ. Это некоторая КНФ f_w, которая обращается в единицу тогда и только тогда, когда на слове w задача Z имеет ответ "да".

Так как задача Z (язык L_Z) лежит в NP, то имеется НМТ T_Z={S, A, F, q₀, d}, решающая эту задачу (допускающая язык L_Z) за полиномиальное от длины входа |w|=n время. Пусть p(n) - полином, ограничивающий число тактов работы NMT. Для простоты индексации будем считать, что подобрано подходящее k, такое что p(n)<n^k.

Идея состоит в том, чтобы смысл данной фразы записать в виде логической формулы. Наглядно представить себе подобную формулу позволяет подробное описание всех шагов вычисления T_Z на входе w. Их легче всего представить в виде таблицы, строки которой - конфигурации работы T_Z на стадии проверки. Такая таблица называется допускающей таблицей и имеет вид.

Номера конфигураций/ячеек

-nk

...

v+1

v

...

-1

0

1

...

n

n+1

...

nk

1

L

…

L

av

…

a1

q0

w1

…

wn

L

…

L

2

...

nk

 

Ее размеры очевидным образом ограничены условием полиномиального времени работы: количество столбцов не превосходит времени работы, а число строк просто равно числу тактов работы НМТ. В первой строке написана отгадка a₁,…,a_v и код слова индивидуальной задачи (слово языка L_Z) w₁,…,w_n . В следующей строке приведена конфигурация НМТ после первого такта ее работы и т.д. Ясно, что построение такой таблицы потребует полиномиального по длине входа n времени.

Грубо говоря, эта таблица будет теперь входом задачи о выполнимости. То есть, по ней мы построим некоторую КНФ, которая выполнима тогда и только тогда, когда данный вход описывает именно таблицу допустимости.

Логика же здесь простая. Должны быть справедливы одновременно четыре утверждения.

1. В каждой клетке таблицы записан ровно один символ, причем это или пустой символ, или буква алфавита A, или символ (номер) состояния из S. (Пусть это условие можно записать в виде некоторой конъюнкции f₀).

2. В первой строке записана начальная конфигурация, например, в том виде, что на рисунке выше. (Пусть это условие можно записать в виде некоторой конъюнкции f_start).

3. В последней строке записана некоторая допускающая конфигурация, т.е. машина остановилась в состоянии q_y. (Пусть это условие можно записать в виде некоторой конъюнкции f_accept).

4. Каждая следующая строка в таблице получается вследствие допустимого перехода МТ. Этот переход осуществляется путем выполнения некоторой команды q_ia_j®q_ra_t{Z},заданной функцией переходов d.(Пусть это условие можно записать в виде некоторой конъюнкции f_computs).

В результате получаем КНФ

f_w = f₀&f_start&f_accept&f_computs.

Если она обращается в единицу, то выполняются все вышеприведенные четыре условия, которые влекут за собой допустимость некоторого корректного вычисления НМТ на индивидуальной задаче w некоторой массовой задачи Z. Набор значений переменных в задаче о выполнимости, на котором КНФ обращается в единицу, и даст нам содержимое допускающей таблицы, которая и описывает данное корректное вычисление.

С другой стороны, если мы имеем некоторое корректное вычисление НМТ на индивидуальной задаче w некоторой массовой задачи Z, то оно может быть представлено в виде допускающей таблицы, по которой строится КНФ

f_w = f₀&f_start&f_accept&f_computs.

И просто по построению эта КНФ должна быть выполнима на том входе, который задает содержимое допускающей таблицы.

Остается построить за полиномильное время четыре вышеупомянутые конъюнкции.

В качестве переменных рассмотрим множество булевских переменных

Var = {x_ijs, i=-n^k,…,n^k; j=-n^k,…,n^k; sÎSÈA}.

Эти переменные обращаются в единицу, если на пересечении i-й строки и j-го столбца допускающей таблицы стоит символ s.

Покажем, что первая из четырех конъюнкций f₀ выражается в следующем виде.

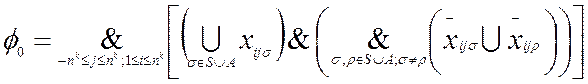
Знак конъюнкции означает, что логическое условие в скобках должно выполняться для каждой клетки таблицы. Первое из условий в круглых скобках соответствует требованию наличия в каждой клетки таблицы хотя бы одного символа (из области значений введенного выше множества переменных Var). То требование, что в клетке должно быть не более одного символа, записано в виде логического выражения во второй круглой скобке формулы для f₀.

Так как число состояний и число символов алфавита являются константами, то длина выражения в скобках от n не зависит. Поэтому длина всей конъюнкции f₀ равна O(n^2k).

Следующая конъюнкция f_start выражается формулой

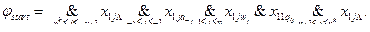
Здесь все понятно. Это просто логическая запись требования к содержимому первой строки таблицы. Для индивидуального входа w и отгадки a оно должно быть именно таким, как показано на рисунке выше. Длина всей конъюнкции f_start равна O(n^k).

Что касается конъюнкции f_accept , то она выражается формулой

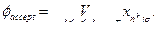
Смысл в том, что в последней строке допускающей таблицы должна стоять конфигурация, содержащая символ конечного состояния. Длина всей конъюнкции f_accept равна O(n^k).

Самым сложным является вычисление конъюнкции f_computs. Мы не будем выписывать его во всей строгости, приведем лишь общую идею формулы. Как уже говорилось выше, эта конъюнкция должна быть формальной записью того условия, что каждая следующая строка в таблице получается вследствие допустимого перехода МТ. А сам переход осуществляется путем выполнения некоторой команды q_ia_j®q_ra_t{Z},заданной функцией переходов d. Обозначим через f_i(i+1) условие того, что правильно осуществлен переход между соседними конфигурациями. Тогда f_computs выглядит следующим образом

Для нахождения f_i(i+1) заметим следующее. Две соседние строки допускающей таблицы различаются не более чем в трех клетках. То есть все изменения сосредоточены в "окошке" таблицы" следующего вида

(i,j-1)	(i,j)	(i,j+1)
(i+1,j-1)	(i+1,j)	(i+1,j+1)

Первая строка таблицы правильно заполнена в силу условия f_start. Заполняем таблицу, начиная со второй строки. Поэтому в паре i-й и (i+1)-й строк проверка того условия того условия, что каждая следующая строка в таблице получается вследствие допустимого перехода МТ, сводится к правильности проверки заполнения (i+1)-й строки. Для этого "проходим" всю пару вышеупомянутыми окошками.

Если в верхней части окошка нет символа состояния, то в нижней части символы алфавита совпадают с верхними. Как только символ состояния встретился, читаем стоящий рядом символ алфавита. Так как число состояний, число букв алфавита и число правил переходы - постоянные величины, то логическое условие, определяющее правильность перехода между соседними конфигурациями, не зависит от n. Действительно, вспомним теорему о полноте базиса из трех булевых функций: &, È и Ø. В качестве простого упражнения можно записать упомянутое условие через эти функции.

Но для построения конъюнкции f_i(i+1) все равно нужно пройти всю строку. Поэтому и длина всей конъюнкции f_computs равна O(n^2k).

Таким образом, все четыре требуемые конъюнкции построены за полиномиальное время.

Теорема доказана.

Итак, у нас появилась первая NP-полная задача. Для доказательства NP-полноты следующей задачи можно либо повторить что-то похожее на только что доказанную теорему, либо использовать понятие сводимости.

Классы NP и co-NP

Для любой Z задачи из NP можно сформулировать дополнительную задачу (язык) Z'. Если язык L_Z образуют все слова, являющиеся условием индивидуальных задач с ответом "да", то язык L_Z' образуют все слова, являющиеся условием индивидуальных задач с ответом "нет". Совокупность таких "дополнительных" задач и составляет класс co-NP. Аналогично для класса P может быть определен класс co-P.

 

Вообще говоря, дополнение множества слов, являющихся условиями индивидуальных задач с ответом "да", содержит два типа слов: слова, являющиеся кодами условиями индивидуальных задач с ответом "нет", и слова, не являющиеся условиями задач.

Предполагается, что последние можно отсеять с помощью каких-то вспомогательных "простых" процедур, например, синтаксических проверок и т.п.

Для любой задачи из класса P дополнение можно получить заменой заключительного состояния (q_no заменяем на q_yes и наоборот). Так как нет никакой угадывающей головки, то на любом корректно заданном условии задачи МТ остановится. Таким образом, мы автоматически получаем из МТ, решающей задачу Z, МТ для решения Z'. Поэтому классы P и co-P совпадают.

Пример. Рассмотрим задачу "Связность графа". Ее входом является неориентированный граф, а вопрос состоит в проверке его связности. Пусть граф G=(V,E) задан списками соседей вершин.

Рассмотрим следующий алгоритм. Берем пустое множество W.

1 шаг. На первом шаге включаем в него некоторую вершину v. Она считается помеченной, но не просмотренной. Переходим ко второму шагу.

2 шаг. Включаем в W всех соседей всех непросмотренных вершин. После этого только вновь включенные вершины считаются помеченными, но непросмотренными. Переходим к шагу 3.

3 шаг. Если W=V, то ответ "да". Если W¹V и непросмотренных вершин нет, то ответ "нет". В остальных случаях переходим к шагу 2.

Ясно, что шагов не более n. И на каждом шаге не более m проверок. Очевидно, что данный алгоритм решает как задачу с вопросом, связен ли G, так и задачу с вопросом, является ли G несвязным.

Для NP и co-NP ситуация иная. Например, обратная к задаче "гамильтонов цикл" задача состоит в ответе на вопрос: "Правда ли, что в данном графе нет гамильтонова цикла?" Как здесь может выглядеть подсказка? На сегодняшний день единственной возможной подсказкой представляется выписывание всех возможных гамильтоновых циклов и проверка их отсутствия в данном графе.

                       

 

Но такой список циклов имеет экспоненциальную длину.

Поэтому вопрос о соотношении NP и co-NP является открытым.

Теорема 9.2. Если существует NP-полная задача Z такая, что ее дополнение лежит в NP, то

NP=co-NP.

Доказательство строится конструктивно с помощью композиции машин Тьюринга.

Пусть дополнение Z' некоторой NP-полной задачи Z лежит в NP. Покажем, что тогда дополнение W' любой задачи W лежит в NP. По определению полиномиальной сводимости функция f, осуществляющая эту сводимость, например, задачи W к задаче Z одновременно осуществляет полиномиальную сводимость задачи W' к задаче Z'. Функция f (одна МТ) вычисляется за полиномиальное время, проверка принадлежности Z' к NP (другая МТ, уже недетерминированная) тоже вычисляется за полиномиальное время. Поэтому проверка принадлежности W' к NP осуществляется путем последовательной комбинации этих двух машин, т.е. может быть проведена за полиномиальное время на недетерминированной МТ.

Классы P-SPACE и NP-SPACE.

Классы P и P/poly.

Рассматриваем, как обычно, задачи в форме распознавания. В начале курса мы говорили о возможности двух принципиально разных подходов к анализу понятия «сложность задачи». Один из них был связан с алгоритмом решения задачи Z, второй – со сложностью СФЭ, реализующих булеву функцию f_Z, значение которой дает ответ на задачу Z в форме распознавания.

Схема доказательства теоремы Кука позволяет легко установить соответствие между классами P и P/poly.

Действительно, для любой задачи из P можно построить допускающую таблицу ее решения на машине Тьюринга так же, как это сделано выше при доказательстве теоремы Кука. По этой таблице мы построим КНФ полиномиальной длины f, а уже для этой КНФ - схему их функциональных элементов, вычисляющую f. Очевидно, что схема будет содержать полиномиальное число вершин. Таким образом, справедливо следующее утверждение.

Теорема 9.1. P Í P/poly.

А что будет, если Z 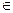P/poly? Оказывается, что класс P/poly шире класса P. Это связано с тем, что существуют алгоритмически неразрешимые проблемы. В курсе дискретной математики вам о них, наверное, рассказывали.

Приведем пример, который, по сути, является известным со времен античности парадоксом брадобрея. В деревне есть брадобрей, который бреет всех, кто не бреется сам. Попробуйте ответить на вопрос, бреет ли он самого себя. При любом ответе получается противоречие.

Облачим теперь этот парадокс в «математическую форму». Проблема остановки (halting problem) состоит в том, чтобы ответить на вопрос (мы о нем говорили выше, когда давали определение машины Тьюринга): остановится или зациклится данная машина Тьюринга T на данном входе x? Оказывается, что, как и в случае брадобрея, любой ответ приводит к противоречию. То есть не существует машины Тьюринга, которая решает проблему остановки.

Теорема. Проблема остановки алгоритмически неразрешима.

Доказательство. От противного. Пусть такая машина T* существует. Тогда на входе (T,x) она выдает ответ «да», если машина Т останавливается на этом входе, и «нет» в противном случае. (Здесь Т – слово в алфавите А, являющееся описанием машины Т). Тогда по Т* можно построить машину Тьюринга T’(x), которая в случае, если T*(x,x)=”да”, начинает двигать головку в одну сторону и зацикливается, а в случае T*(x,x)=”нет” она останавливается. Что в этом случае будет означать T’(T’)? Остановится или нет машина на этом входе? Если «да», то это означает, что T*(T’)= «нет», т.е. T’ не должна останавливаться на T’. Если «нет», то это означает, что T*(T’)= «да», т.е. T’  должна останавливаться на T’.

Получили противоречие

Теорема доказана.

Рассмотрим функцию натурального аргумента f(n), принимающую значения 0 или 1. Можно показать, что вычисление такой функции может быть алгоритмически неразрешимой проблемой, т.е. не входит такая задача ни в какой класс сложности, а не только в класс P. Рассмотрим теперь предикат A_f(x)=f(|x|). Для любого фиксированного n предикат равен константе. А константе сопоставляется СФЭ, сложность которой тоже равна константе. Поэтому  A_f(x) 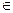P/poly, но его вычисление может быть алгоритмически неразрешимой проблемой.

Конечно, все это связано с тонкостями определений математических объектов и тем, что при вычислении предикатов основная сложность может лежать не в логических операциях, а в вычислении термов, от которых зависит предикат. Это вычисление связано с интерпретацией и допускает наличие в качестве аргумента предиката произвольной, сколь угодно сложновычислимой функции.

Результатом этого рассмотрения является следующая простая теорема (см. [6]).

Пусть задача Z в форме распознавания эквивалентна вычислению булевой функции f. Суть в том, что с ростом числа переменных n=1,2,… мы имеем последовательность формул f_n и схем S_n для этой функции. И именно свойства такой последовательности для нас выжны.

Теорема. Функция (задача) f 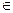P тогда и только тогда, когда f 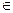P/poly и существует машина Тьюринга, которая за полиномиальное от длины входа n время строит СФЭ для f_n.

Для доказательства заметим следующее. Теорема Кука дает конструктивный метод построения СФЭ полиномиального по входу размера за полиномиальное по входу время для функции f 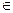P. Т.е. в этом случае f 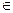P/poly и за полиномиальное от длины входа n время строястя СФЭ для f_n.

И наоборот, если f 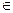P/poly и существует Т - машина Тьюринга, которая для каждого отдельного n за полиномиальное от длины входа время по n строит СФЭ S_n для f_n. Вычислений значения функции по этой схеме тоже потребует не более, чем полиномиального времени.

Грубо говоря, с точностью до «разницы в определениях» двух подходов: алгоритмического и схемного, можно представлять себе классы P и P/poly достаточно близкими. Про соотношение классов P и NP мы ничего не знаем. А вот на вопрос, как соотносится класс P/poly с классом всех СФЭ, ответ дает теорема Лупанова. Почти все схемы имеют экспоненциальную сложность 2ⁿ/n, т.е. множество функций (задач в форме распознавания), имеющих СФЭ полиномиального размера , пренебрежимо мало. Этот результат создал иллюзию безысходности в области исследований по алгоритмической сложности в 1960-е годы. На этом фоне результат Кука (1971 год) явился определенным идеологическим прорывом в том смысле, что он обратил внимание исследователей на небезнадежность решения задач, принадлежность которых к классу NPC не удалось доказать после достаточно серьезных усилий квалифицированных специалистов. И хотя таких задач было решено немного (пионером здесь является Л.Г.Хачиян , решивший за полиномиальное время задачу линейного программирования), но каждое из таких решений явилось фундаментальным достижением в математике.

Некоторые результаты

Обозначим через SPACE(f(n)) класс задач (языков), для которых существует МТ, работающая на памяти с объемом, ограниченным f(n).

Аналогично NSPACE(f(n)) класс задач (языков), для которых существует НМТ, работающая на памяти с объемом, ограниченным f(n).

Приведем без доказательства следующее утверждение, уточняющее некоторые из вышеприведенных.

Теорема 9.7. NSPACE(f(n))ÍSPACE(f(n)²).

Приближенные алгоритмы

Понятие приближенный алгоритм мы будем использовать только для алгоритмов решения задач в оптимизационной форме.

Опр. Пусть дана задача Z=(F, c) и – c(x*) значение функции стоимости c на оптимальном решении x*. Пусть дан некоторый алгоритм W, результатом работы которого будет выдача некоторого решения x’, а c_W(x’)– значение функции стоимости на решении x’. Будем говорить, что алгоритм W является ε-приближенным (или алгоритмом с оценкой точности ε), если выполняется следующее соотношение:|( c_W(x’)- c(x*))/ c(x*) |≤ ε.

Опр. Пусть дана задача Z=(F, c) и – c(x*) значение функции стоимости c на оптимальном решении x*. Пусть дан некоторый алгоритм W, результатом работы которого будет выдача некоторого решения x’, а c_W(x’)– значение функции стоимости на решении x’. Будем говорить, что алгоритм W является эвристическим, если про соотношение c_W(x’) и c(x*) ничего не известно.

Часто эвристические алгоритмы называют приближенными без оценки точности. Примером эвристического алгоритма для задачи коммивояжера называется жадный алгоритм или алгоритм иди в ближайшую.

Пример. Дана задача коммивояжера на n городах с матрицей попарных расстояний. Будем строить решение x’ следующим образом.

Из вершины 1 идем в вершину i₁ такую, что ребро (1,i₁) имеет минимальный вес среди всех ребер вида (1,j), на втором шаге из вершины i₁ идем в вершину i₂ 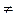1 такую, что ребро (i₁,i₂) имеет минимальный вес среди всех ребер вида (i₁,j), j 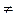1; из вершины i₂ идем в вершину i₃ 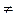1, i₂ такую, что ребро (i₂,i₃) имеет минимальный вес среди всех ребер вида (i₂,j), j 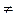1,i₂.  И так далее. На последнем шаге замыкаем цикл.

Легко привести пример того, что этот алгоритм может не находить оптимального решения. Трудоемкость алгоритма не превосходит  O(n²), но мы ничего не можем сказать про соотношение c_W(x’) и c(x*).

А как обстоят дела с приближенными алгоритмами для этой задачи?

Теорема. Если P 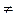NP, то при любом ε >0 не существует ε – приближенного алгоритма для задачи коммивояжера.

Доказательство. От противного. Пусть такой алгоритм W для некоторого ε >0 существует. Покажем, что тогда P=NP. Для этого мы докажем, что алгоритм W решает задачу гамильтонов цикл. Так как эта последняя является NP-полной, то отсюда и будет следовать равенство P=NP.

Пусть входом задачи гамильтонов цикл является граф G=(V,E). Постоим на его основе условие некоторой вспомогательной задачи коммивояжера на |V| городах, а расстояние между городами i и j положим равным 1, если ребро (i,j) есть в графе G, и равным 2+ ε|V|, если такого ребра в графе нет.

Применим наш полиномиальный алгоритм W для получения ε –приближенного решения вспомогательной задачи коммивояжера. Докажем, что этот алгоритм выдаст обход коммивояжера длины |V| тогда и только тогда, когда в G есть гамильтонов цикл. Очевидно, что, если такой обход выдан, то каждое ребро в нем имеет длину единица, т.е. соответствует ребру графа G, а выданный обход, таким образом, гамильтонову циклу этого графа. И наоборот, если в графе G есть гамильтонов цикл, то алгоритм обязательно выдаст обход длины |V| потому, что в случае выдачи любого другого обхода (а в этом случае минимальное значение длины такого обхода не меньше |V|-1+2+ ε|V|) нарушается свойство ε –приближенности алгоритма:

(|V|-1+2+ ε|V|-|V|)/|V|=1/|V|+ ε > ε.

Теорема доказана.

В некотором смысле ситуация с приближенными алгоритмами для задачи коммивояжера типична для NP-трудных задач: полиномиальные эвристические алгоритмы всегда есть, а полиномиальных приближенных (для общего случая) нет.

Теорема. Если для задачи о клике существует ε – приближенный алгоритм для некоторого ε>0, то тгда для этой задачи можно будет построить ε – приближенный алгоритм для любого 1> ε>0.

Однако, в отличие от точных алгоритмов, полиномиальные приближенные можно построить для интересных частных случаев NP-трудных задач. Например, для задачи коммивояжера с неравенством треугольника (для любых трех вершин i,j,k длина ребра (i,j) не превосходит суммы длин ребер (i,k)и (k,j)) существуют приближенные алгоритмы. Одним из самых первых был 1/2-приближенный алгоритм Кристофидеса.

Мы видим, что с практической точки зрения, если вам нужно решать –трудную задачу, сложность точного и приближенного решения для общего случая одинакова, поэтому или вам надо искать в своей задаче какие-то особенности, которые сведут ее к частному случаю, либо пользоваться методами направленного перебора.

Коммуникационная сложность

Этот подход к оценке сложности задач в некотором смысле связан с предыдущим и, так же как и параллельные вычисления, обусловлен, в первую очередь, развитием компьютерной техники.

В случае параллельных вычислений основная забота – эффективно использовать вычислительный ресурс. В модели параллельных вычислений процессоры обмениваются информацией. Время обмена информацией и стоимость такого обмена полагается пренебрежительно малой по сравнению со временем и стоимостью вычислений.

Если же поменять акценты на противоположные: время и стоимость вычислений пренебрежительно мала по сравнению временем обмена информацией и стоимостью такого обмена – получаем подход, называемый коммуникационной сложностью. Обсчет сложных физических экспериментов научными центрами, обмен информацией между гидрометцентрами в реальном времени для составления прогноза погоды и т.п. – это реальные современные задачи, которые встают в условиях распределенных хранилищ информации, критичности времени обмена и не всегда разумной стоимостью трафика как коммуникационного ресурса.

Так же, как и в случае параллельных вычислений, модель коммуникационного взаимодействия между хранилищами информации в процессе совместного решения конкретной индивидуальной задачи – это предмет постановки задачи. Такая модель обычно связывается с понятием коммуникационного протокола. Три основных группы параметров модели связаны со следующими ее составляющими.

1. Участники. Это процессоры (ФУ, серверы, ЛВС предприятий и т.п.), осуществляющие вычисления (обработку информации) на местах (в точках распределенной сети). Они могут быть равноправны и неравноправны, потребность в информации (обращении) каждого участника со стороны остальных может быть разной и т.д.

2. Линии связи. Стоимость обмена данными может зависеть от конкретной пары обменивающихся участников. Она может быть несимметричной. Пропускная способность канала связи может быть ограниченной и пр.

3. Ограничения на возможности (правила) обмена информацией. Не все участники могут одновременно получать и отправлять информацию (кто-то может делать только одно из этих действий). Друг с другом можно связать только определенные пары участников. И т.д.

Все эти параметры в модели вычислений должны быть оговорены и тогда они станут частью протокола вычислений, который на их основе опишет правила работы получившейся распределенной вычислительной системы. Те, кто работал с СУБД, сразу смогут увидеть здесь аналогию этого протокола с протоколами обработки распределенной базы данных.

В теории сложности в качестве базового случая рассматривается простейший: два равноправных участника (Алиса и Боб) с симметрично распределенной между ними входной информацией совместно вычисляют булеву функцию f(x₁,…,x_n), обмениваясь в процессе вычисления сообщениями фиксированной длины (они называются битами). Процесс обмена представляется корневым ориентированным деревом (корень ассоциируется с инициатором обмена), каждая промежуточная вершина которого соответствует участнику посылающему информацию, висячая вершина – результату вычислений, а ребро значению бита (0 или 1). Такое дерево называется протоколом вычисления функции f, а длиной протокола называется максимум длины пути в этом дереве. Вообще говоря, даже в нашем простейшем случае можно построить разные протоколы (как можно построить разные машины Тьюринга для решения одной и той же задачи), поэтому формально определение коммуникационной сложности для рассматриваемой модели вычислений выглядит следующим образом.

Опр. Коммуникационная сложность вычисления функции – это минимум по длинам всех протоколов, вычисляющих эту функцию.

Получаем такой min- max –ый критерий. До сих пор мы имели дело с  max- min-ми критериями: определение сложности «в худшем», функция Шеннона и пр.

Ниже приведен пример совместной проверки участниками равенства x₁y₂=x₁y₂.

Очевидно, что в нашей простейшей модели коммуникационная сложность любой задачи не превосходит O(n) (здесь n, как обычно, обозначает длину входа задачи). Действительно, тривиальный протокол, состоящей в единичной посылке своих данных одним участником другому приводит к вычислению функции. (Еще раз подчеркнем, что в нашей модели трудоемкость самих вычислений равна нулю).

Приведем несколько примеров задач. Коммуникационная сложность которых может быть меньше O(n).

Пример. Задача «четность». Дано два булевых вектора: x (находится у Алисы) и  y (находится у Боба). Определить четность длины вектора конкатенации xy.

Задача решается за О(1) путем посылки четности своей части одним участником другому.

Пример. Задача «сумма бит». Дано два булевых вектора одинаковой длины n: x (находится у Алисы) и  y (находится у Боба). Определить, одинаково ли число единиц в этих векторах.

Задача решается за О(logn) очевидным образом путем посылки суммы единиц  своей части одним участником другому.

Пример. Задача «эквивалентность». Дано два булевых вектора одинаковой длины n: x (находится у Алисы) и  y (находится у Боба). Определить эквивалентны ли они.

Задача решается за О(n) тривиальным алгоритмом путем посылки своего вектора одним участником другому. Оказывается, что ее нельзя решить быстрее. Это, в каком-то смысле тривиальное следствие теоремы Шеннона из теории информации. Вектора битовые. Каждый участник должен получить информацию о каждом бите, но нельзя бит закодировать информацией меньшей длины, чем один бит.

Но это тривиальные примеры. Учебник по коммуникационной сложности начинается, обычно, со следующего, менее очевидного примера.

Пример. Задача «медиана». Медианой упорядоченного числового множества из n  элементов называется элемент этого множества, стоящая на ]n/2[ месте. Алиса и Боб имеют по одному подмножеству множества {1,2,…,n}. Требуется найти медиану объединения подмножеств Алисы и Боба.

Легко построить алгоритм решения со сложностью O(log²n). Для этого заметим, что медиана всего множества лежит между медианами частей Алисы и Боба. Вначале Боб посылает Алисе свою медиану, Алиса в ответ посылает ему медиану той части своего множества, которая лежит между ее медианой и медианой Боба и т.д. Получаем сходящуюся дихотомию, в которой не больше O(logn) шагов и на каждом шаге посылается O(logn) битов.

Однако можно построить и более экономный алгоритм сложности O(logn).

Рассматриваются и более общие (по сравнению с моделью Алиса-Боб) модели. Они, как правило, имеют практическое обоснование и учет их специфики приводит либо к тривиальным результатам, либо требует решения технически сложных задач на стыке комбинаторной математики и теории телекоммуникационных протоколов. Важно, что вы должны знать о существовании таких постановок и при столкновении с ними в своей будущей инженерной деятельности сможете, при желании, найти результаты тридцатилетних исследований в этой области. А, если эти результаты вам не помогут, то можете переквалифицироваться в математиков и попытаться внести свой вклад в эти исследования.

 

Заключение

Предложенный здесь текст обладает рядом свойств.

1. Он является базовым как для объема 17 лекций – 17 семинаров (для студентов по программе «специалист», так и для объема 17 лекции – 9 семинаров (для магистратуры).

2. Сам материал является классическим и в той или иной мере присутствует в аналогичных курсах ведущих Вузов России. Однако, подбор материала, логика изложения и акценты ориентированы на специфику подготовки студентов кафедры ИУ-8.

3. Для студентов, желающих углубить и расширить свои знания в этой области, автор постарался привести (в минимальном объеме) необходимые источники, освоение которых должно быть не очень затруднительным при условии овладения предлагаемым здесь текстом лекций.

4. Предполагается, исходя из методического плана подготовки на кафедре ИУ-8, что студент, освоивший предмет в полной мере, готов к пониманию курсов «Алгоритмы и структуры данных» и «Исследование операций».

5. Во многом тематика данного курса явилась поводом для изложения в нем подготовительных материалов для другой дисциплины- курса по выбору: «Дополнительные главы теории сложности алгоритмов».

13. Задачи и вопросы для самопроверки по курсу «Математическая логика и теория алгоритмов».

Задачи.

Задача 1.1 Написать на любом языке алгоритм находящий минимальное из n чисел и оценить его трудоемкость.

Задача 1.2 Написать на любом языке алгоритм сортирующий n чисел и оценить его трудоемкость.

Задача 1.3 Для заданного графа с 8 вершинами построить примеры: цикла, контура, гамильтонова цикла, клики, вершинного покрытия.

Задача 1.4 Написать на любом языке алгоритм распознавания простоты натурального n и оценить его трудоемкость.

Задача 1.5 Для 6 камней с заданными весами написать алгоритм решения задачи о камнях и оценить его трудоемкость.

Задача 2.1 Построить НАМ f(x)= 3.

Задача 2.2 Построить НАМ f(x,y)=x+êx-yú.

Задача 2.3 Построить НАМ f(x,y,z)=z+êx-yú.

Задача 2.4 Построить НАМ, преобразующую слово P в слово PP.

Задача 3.1 . Построить МТ, вычисляющую функцию f(x,y,z)=z.

Задача 3.2. Построить МТ, вычисляющую функцию f(x)=x+1.

Задача 3.3. Построить МТ, вычисляющую функцию f(x,y)=x+y.

Задача 3.4. Построить МТ, вычисляющую функцию f(x,y,z)=z+êx-yú.

Задача 4.1. Построить МТ, записывающую буквы любого слова некоторого конечного алфавита в обратном порядке.

Задача 4.2. Построить МТ, преобразующую слово P в слово PP.

Задача 4.3. Для входного алфавита {b, c} построить МТ, "различающую" слова, содержащие b от остальных.

Задача 4.4 Определена машина Тьюринга (см. лекции) T = {S, A, F, q₀, d}, d - упорядоченная последовательность команд. Доказать, что определение МТ эквивалентно определению, в котором команды перехода - L, R, St – включены в алфавит. (Докажите это в виде простого упражнения.).

Задача 5.1 Для функции f построить схему в базисе B.

· f= xÚy, B={Ù,»}.

· F=xÅyz, B={®,ù}.

Задача 5.2. Для системы функций построить схему в базисе B.

· F=xyÚxzÚzy, g=xÅzÅy; B={Å,Ù}.

· F=ùx, g=ùxùy, h=1, T=ùxùzùy; B={ù,¯}.

Задача 5.2. Для функции f построить схему сложности не выше m в базисе B={Ù,Ú,ù}.

· f=x»y, m=4.

· F=ùxùy, m=2.

Задача 6.1. Доказать, что задача "гамильтонов цикл" сводится к задаче "коммивояжер".

Задача 6.2 Доказать, что задача "КНФ выполнимость" сводится к задаче "клика".

Задача 6.3 Доказать, что задача «3-выполнимости" сводится к задаче "ЦЛП".

Задача "ЦЛП" (целочисленного линейного программирования) :

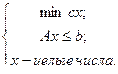
Задача 7.1. Доказать полиномиальную разрешимость задачи «2-КНФ».

Задача 7.2. Доказать NP- полноту задачи «вершинное покрытие». ( Вершины вершинного покрытия содержатся во всех ребрах графа).

Задача 8.1 Для задач из класса NP, рассмотренных на предыдущих трех занятиях, сформулировать соответствующие задачи из класса co-NP.

Задача 8.2 Для алгоритмов, рассмотренных на Занятии 1 оценить используемую память.

Задача 8.3 Для задачи «k-е по порядку подмножество» оценить используемую память.

Вопросы.

· Понятие «задача». Форма задачи. Индивидуальная и массовая задача. Привести примеры.

· Определение Машины Тьюринга (МТ). Различие детерминированной и недетерминированной МТ.

· Определение Оракульной Машины Тьюринга (ОМТ). Различие оракульной и недетерминированной МТ.

· Определение Недерминированной Машины Тьюринга (НМТ). Привести пример.

· Задание «входа» для индивидуальной задачи. Примеры кодировок графов. Понятие полиномиальной эквивалентности для различных кодировок объекта.

· Классы  P, NP, NPC. Соотношение между ними.

· Привести примеры выполнимой и общезначимой формулы в исчислении предикатов.

· Классы  PSPASE, NPSPASE. Соотношение между ними.

· Классы  PSPASE, EXPTIME. Соотношение между ними.

· Определение СФЭ. Пример СФЭ.

· Классы  P/Poly и P. Соотношение между ними.

· Построить НАМ для обращения слов в заданном алфавите.

· Класс  PSPASE и игра двух лиц. Соотношение между ними.

· По заданной формуле в исчислении предикатов построить формулу в приведенной нормальной форме.

· Отношения. Сводимость по Тьюрингу.

· Примеры полиномиально разрешимых частных случаев NP –полных задач.

· Предикат. Формула в исчислении предикатов. Выполнимые и общезначимые формулы. Приведенная нормальная форма.

· Теорема Кука. Схема доказательства.

· Понятие алгоритма. Эквивалентность алгоритмов. Тезис Черча.

· Алгоритм нахождения кратчайшего пути между вершинами графа.

· Примеры подходов к решению NP-полных задач.

· Определение полиномиальной сводимости и сводимости по Тьюрингу. Пример полиномиальной сводимости.

· Теорема о PSPACE-полной задаче.

· Классы NP и co-NP. Соотношение между ними. Теорема об  NP–полной задаче и классе Co-NP.

· Приближенные алгоритмы с оценкой точности. Теорема о существовании такого алгоритма для «Задачи коммивояжера».

· Игра двух лиц. Определение. Игра двух лиц и классы NP и co-NP.

· Коммуникационная сложность. Коммуникационная сложность задачи о равенстве числа единиц в двух булевских векторах.

· По заданной формуле в исчислении предикатов построить формулу в приведенной нормальной форме.

 

14. Рекомендованная литература

1. Ахо А.А., Хопкрофт Д.Э., Ульман Д.Д. Структуры данных и алгоритмы. М.: Вильямс, 2007. – 400 с.

2. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 2012.

3. Мендельсон Э. Введение в математическую логику. М.: Наука, 2012.

4. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. М.: Мир, 1984.

5. Гордеев Э.Н. Задачи выбора и их решение. – Сб. «Компьютер и задачи выбора. М.: Наука, 1989.

6. Кузюрин Н.Н., Фомин С.А. Эффективные алгоритмы и сложность вычислений.М: МФТИ, 2007.

7. Лупанов О.Б. Курс лекций по дискретной математике. - Конспект лекций. МГУ. 2012.

 

Э.Н.Гордеев

 

ВВЕДЕНИЕ В ТЕОРИЮ СЛОЖНОСТИ АЛГОРИТМОВ.

Учебное пособие

 по дисциплине «Математическая логика и теория алгоритмов».

 

 

Москва

(С) 2016 МГТУ им. Н.Э. БАУМАНА

 

УДК 519.7

Гордеев Э.Н.

Введение в теорию сложности алгоритмов. Электронное учебное издание. - М.: МГТУ имени Н.Э. Баумана, 2016. 128 с.

Издание содержит конспект лекций по курсу «Математическая логика и теория алгоритмов», предусмотренного учебным планом МГТУ им. Н.Э.Баумана. Представлены формальные модели алгоритмов, рассмотрены различные подходы к понятию сложность задачи. Описаны наиболее известные классы сложности задач. Приведены примеры исследования сложности известных задач.

Для студентов факультета «Информатики и систем управления» МГТУ имени Н.Э. Баумана.

 

Рекомендовано учебно-методической комиссией НУК «Информатики и систем управления» МГТУ им. Н.Э. Баумана

 

Гордеев Эдуард Николаевич