На рис. 1. приведены результаты расчетов величины баротермического эффекта от времени при различных барических сжимаемостях. В расчетах принято: ε=-0.5∙10-5 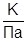 ; r=0.1
; r=0.1 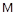 ; с=850
; с=850 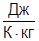 ; k=10-15
; k=10-15 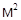 ; сPL=84000000
; сPL=84000000 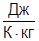 ; µ=10-5
; µ=10-5 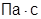 ; R=100
; R=100 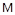 ; ρ=150
; ρ=150 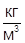 ; α=10-7
; α=10-7  ; P=100∙105
; P=100∙105 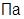 ; P0=150∙105
; P0=150∙105  ; PC=200∙105
; PC=200∙105 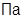 ; PW=150∙105
; PW=150∙105  .
.
Из рисунка видно, что изменение температуры подчиняется следующим закономерностям. Линейное нарастание температурного эффекта при малых временах сменяется логарифмической стабилизацией - при больших временах. Время, при котором происходит смена линейного нарастания на логарифмическую стабилизацию, зависит от барической сжимаемости; с увеличением сжимаемости это время уменьшается.
 Величина температурного эффекта также сильно зависит от сжимаемости. С увеличением сжимаемости величина температурного эффекта возрастает. Коэффициент барической сжимаемости приблизительно обратно пропорционален давлению. Реальные значения этого коэффициента в условиях газовых пластов лежат в пределах от 3 10-8 Па-1 до 10-5; поэтому величина эффекта лежит в пределах до –10 ¸ –15 К.. Это хорошо согласуется с величиной измеряемых в скважинных условиях температурных эффектов.
Величина температурного эффекта также сильно зависит от сжимаемости. С увеличением сжимаемости величина температурного эффекта возрастает. Коэффициент барической сжимаемости приблизительно обратно пропорционален давлению. Реальные значения этого коэффициента в условиях газовых пластов лежат в пределах от 3 10-8 Па-1 до 10-5; поэтому величина эффекта лежит в пределах до –10 ¸ –15 К.. Это хорошо согласуется с величиной измеряемых в скважинных условиях температурных эффектов.

| Рис.1. Зависимость величины баротермического эффекта от времени при различных барических сжимаемостях. Обозначения: 1 - a = 3 10-4 Па-1, 2 – 10-5, 3 – 10-6, 4 – 10-7, 5 – 5 10-8 |
Важно отметить, что согласно разработанной нами теории время установления температурного эффекта при a ~ 10-8 Па-1, что часто встречается на практике, составляет около суток. Этот факт чрезвычайно важен при практическом использовании баротермического эффекта.
На рис. 2 показана зависимость баротермического эффекта от времени при различных относительных вязкостях. Из рисунка видно, что величина температурного эффекта возрастает со временем тем больше, чем меньше относительная вязкость. В расчетах принято: ε=-0.5∙10-5 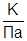 ; r=0.1
; r=0.1 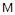 ; с=850
; с=850 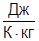 ; k=10-15
; k=10-15 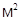 ; сPL=84000000
; сPL=84000000 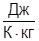 ; µ=10-5
; µ=10-5 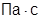 ; R=100
; R=100 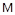 ; ρ=150
; ρ=150 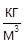 ; α=10-7
; α=10-7 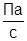 ; P=100∙105
; P=100∙105 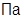 ; P0=150∙105
; P0=150∙105  ; PC=200∙105
; PC=200∙105  ; PW=150∙105
; PW=150∙105  .
.
 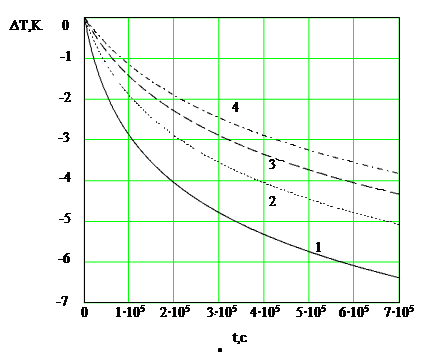
| Рис 2. Зависимость нестационарной температуры от времени при различных относительных вязкостях. Обозначения: 1- µ = 10-5 ; 2 - 2∙10-5 ; 3 – 3∙10-5 ; 4 - 4∙10-5 |
На рис. 3. показана зависимость баротермического эффекта от времени при различных относительных проницаемостях. Из рисунка видно, что величина температурного эффекта возрастает со временем тем больше, чем больше относительная проницаемость. В расчетах принято: ε=-0.5∙10-5  ; r=0.1
; r=0.1  ; с=850
; с=850 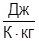 ; сPL=84000000
; сPL=84000000 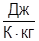 ; µ=10-5
; µ=10-5 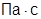 ; R=100
; R=100 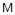 ; ρ=150
; ρ=150 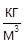 ; α= 10-7
; α= 10-7 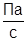 ; P=100∙105
; P=100∙105 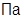 ; P0=150∙105
; P0=150∙105 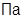 ; PC=200∙105
; PC=200∙105 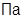 ; PW=150∙105
; PW=150∙105  .
.

| Рис 3. Зависимость нестационарной температуры от времени при различных относительных проницаемостях.Обозначения:1- k = 10-15 м2; 2 -2∙10-15 ; 3 – 3∙10-15; 4 -4∙10-15 |
На рис. 4 показана зависимость баротермического эффекта от времени на различных расстояниях от оси скважины. Из рисунка видно, что величина температурного эффекта возрастает со временем тем больше, чем меньше радиус скважины. В расчетах принято: ε=-0.5∙10-5  ; с=850
; с=850  ; k=10-15
; k=10-15 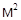 ; сPL=84000000
; сPL=84000000 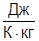 ; µ=10-5
; µ=10-5 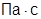 ; R=100
; R=100 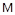 ; ρ=150
; ρ=150 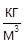 ; α=10-7
; α=10-7 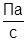 ; P=100∙105
; P=100∙105 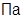 ; P0=150∙105
; P0=150∙105  ; PC=200∙105
; PC=200∙105  ; PW=150∙105
; PW=150∙105  .
.
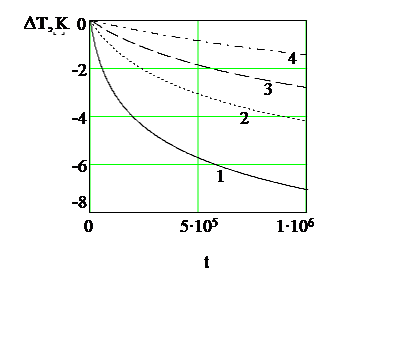
| Рис 4. Зависимость нестационарной температуры от времени при различных радиусах скважины. Обозначения: 1- r =0.1 м ; 2 -0.2 ; 3 – 0.3; 4 -0.5. |
На рис. 5. показана зависимость баротермического эффекта от радиуса скважины при различных временах. Из рисунка видно, что величина температурного эффекта убывает со временем. Чем меньше радиус скважины, тем больше величина температурного эффекта, при увеличении радиуса скважины температурный эффект уменьшается и стабилизируется. В расчетах принято: ε=-0.5∙10-5 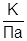 ; с=850
; с=850 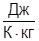 ; k=10-15
; k=10-15 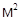 ; сPL=84000000
; сPL=84000000 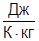 ; µ=10-5
; µ=10-5 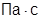 ; R=100
; R=100 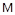 ; ρ=150
; ρ=150 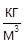 ; α=10-7
; α=10-7 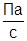 ; P=100∙105
; P=100∙105 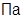 ; P0=150∙105
; P0=150∙105 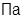 ; PC=200∙105
; PC=200∙105 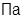 ; PW=150∙105
; PW=150∙105 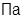 .
.
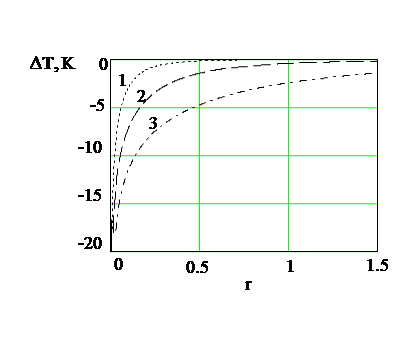
| Рис 5. Зависимость нестационарной температуры от радиуса скважины при различных временах. Обозначения: 1- t =10 000 с; 2 -100 000 ; 3 – 1 000 000. |
На рис. 6. показана зависимость баротермического эффекта от времени при различных радиусах контура питания. Из рисунка видно, что величина температурного эффекта убывает при увеличении радиуса контура питания. В расчетах принято: ε=-0.5∙10-5 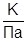 ; rW=0.1
; rW=0.1 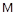 ; с=850
; с=850  ; k=10-15
; k=10-15 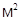 ; сPL=84000000
; сPL=84000000 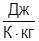 ; µ=10-5
; µ=10-5 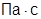 ; ρ=150
; ρ=150 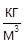 ; α=10-7
; α=10-7 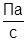 ; P=100∙105
; P=100∙105 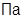 ; P0=150∙105
; P0=150∙105 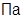 ; PC=200∙105
; PC=200∙105 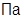 ; PW=150∙105
; PW=150∙105 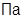 .
.
На рис. 7. показана зависимость баротермического эффекта от теплоёмкости при различных временах. В расчетах принято: ε=-0.5∙10-5 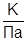 ; rW=0.1
; rW=0.1 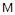 ; k=10-15
; k=10-15 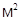 ; сPL=84000000
; сPL=84000000 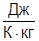 ; µ=10-5
; µ=10-5  ; R=100
; R=100 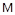 ; ρ=150
; ρ=150 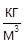 ; α=10-7
; α=10-7 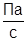 ; P=100∙105
; P=100∙105  ; P0=150∙105
; P0=150∙105 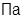 ; PC=200∙105
; PC=200∙105  ; PW=150∙105
; PW=150∙105  .
.
Из рисунка видно, что величина температурного эффекта возрастает при увеличении теплоемкости.
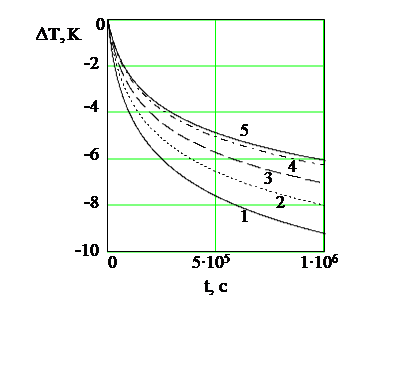
| Рис 6. Зависимость нестационарной температуры от времени при различных радиусах контура питания. Обозначения: 1- R =25 м ; 2 - 50 ; 3 – 100 ; 4 - 200; 5 - 250 . |
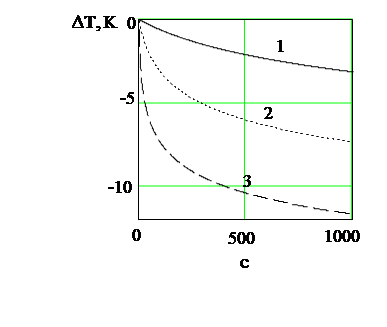
| Рис 7. Зависимость нестационарной температуры от теплоёмкости при различных временах. Обозначения: 1- t =100 000 c ; 2 -1 000 000; 3 – 10 000 000. |
На рис. 8. показана зависимость баротермического эффекта от относительной вязкости при различных временах. Из рисунка видно, что величина температурного эффекта возрастает при уменьшении относительной вязкости. В расчетах принято: ε=-0.5∙10-5  ; rW=0.1
; rW=0.1 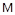 ; с=850
; с=850 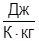 ; k=10-15
; k=10-15 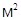 ; сPL=84000000
; сPL=84000000 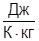 ; R=100
; R=100  ; ρ=150
; ρ=150 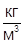 ; α=10-7
; α=10-7 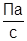 ; P=100∙105
; P=100∙105 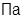 ; P0=150∙105
; P0=150∙105 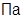 ; PC=200∙105
; PC=200∙105  ; PW=150∙105
; PW=150∙105  .
.
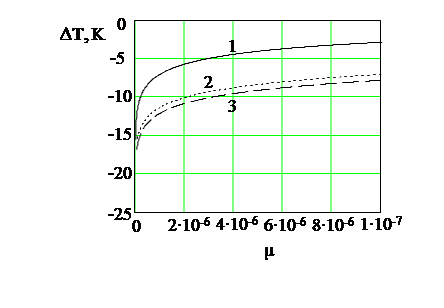
| Рис 8. Зависимость нестационарной температуры от относительной вязкости при различных временах. Обозначения: 1- t =100 000 c ; 2 -1 000 000; 3 – 1 500 000. |
На рис. 9. показана зависимость баротермического эффекта от времени при различных коэффициентах барической сжимаемости. Из рисунка видно,
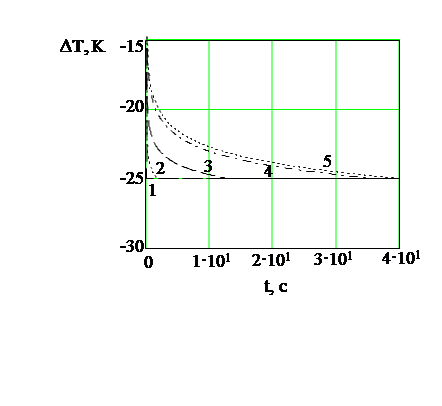
| Рис 9. Зависимость нестационарной температуры от времени при различных коэффициентах барической сжимаемости. Обозначения: 1- α =0,0003 Па-1; 2 -0,00001; 3 -0,000001; 4 -0,0000001;5 – 0,0000005. |
что при уменьшении барической сжимаемости величина температурного эффекта уменьшается. В расчетах принято: ε=-0.5∙10-5  ; rW=0.1
; rW=0.1  ; с=850
; с=850 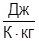 ; k=10-15
; k=10-15 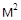 ; сPL=84000000
; сPL=84000000 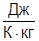 ; µ=10-5
; µ=10-5 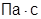 ; R=100
; R=100 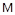 ; ρ=150
; ρ=150 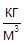 ; P=100∙105
; P=100∙105 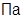 ; P0=150∙105
; P0=150∙105 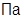 ; PC=200∙105
; PC=200∙105 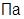 ; PW=150∙105
; PW=150∙105 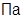 .
.
Дата: 2019-07-30, просмотров: 409.