Модель идеального газа хорошо описывает свойства газообразного состояния вещества при средних и высоких температурах (от комнатной и выше) и небольших давлениях (около атмосферного). Расчет свойств газов в широком интервале экспериментальных условий требует использования уравнения состояния реального газа[1].

Реальным газом называется газ, между молекулами которого существуют заметные силы межмолекулярного взаимодействия. Оно имеет электромагнитную и квантовую природу и осуществляется посредством сил межмолекулярного притяжения и отталкивания.

Силы притяжения, проявляющиеся на расстояниях r между центрами молекул порядка 10^-7 см, называются ван-дер-ваальсовыми силами. Они убывают с расстоянием ~ r ^–7, что соответствует изменению потенциальной энергии по закону r ^–6.

Различают три вида ван-дер-ваальсовых сил [7]:

Ориентационные силы между двумя молекулами, обладающими постоянными дипольными моментами. Они стремятся расположить молекулы упорядоченно так, чтобы векторы дипольных моментов ориентировались вдоль одной прямой. Этому препятствует тепловое движение молекул.

Индукционные силы, возникающие между молекулами, обладающими высокой поляризуемостью. Если молекулы достаточно сближены, то под действием электрического поля одной из них в другой возникает индуцированный дипольный момент.

Дисперсионные силы возникают в результате возбуждения колебаний электронов в молекуле (атоме) под влиянием колебаний электронов в другой молекуле (атоме). Колебания электронов соседних молекул происходят в одинаковой фазе и приводят к притяжению двух молекул (атомов). Величина дисперсионных сил определяется нулевой энергией молекул (атомов), если их колебания можно рассматривать как колебания линейных гармонических осцилляторов.

Полная потенциальная энергия ван-дер-ваальсовых сил описывается суммой:

Для полярных молекул основную роль играют ориентационные силы притяжения, для остальных молекул – дисперсионные силы. Энергия ван-дер-ваальсового притяжения составляет (0,1 – 1) ккал/моль [7]. В большинстве случаев ван-дер-ваальсовы силы притяжения перекрываются значительно превосходящими их химическими валентными силами притяжения с энергиями порядка (10 – 100) ккал/моль.

Согласно упрощенной модели ван-дер-ваальсовых сил, молекулы газа – абсолютно упругие шары – притягиваются с силами, достигающими наибольшего значения при непосредственном их соприкосновении. Силы отталкивания проявляют себя на значительно меньших расстояниях.

Для описания свойств реальных газов применяют различные уравнения состояния, отличные от уравнения Клапейрона-Менделеева. Наиболее удобны двухпараметрические уравнения, разрешимые относительно давления и содержащие объем в третьей степени (кубические уравнения состояния). Первое такое уравнение было предложено Ван-дер-Ваальсом в 1873 г.

Уравнение Ван-дер-Ваальса состояния реального газа имеет следующий вид [7]:

,

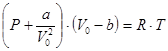(I.1.2)

где V₀ – объем 1 моля газа, а  – внутреннее давление, обусловленное силами притяжения между молекулами, b – поправка за собственный объем молекул, учитывающая действие сил отталкивания между молекулами и равная учетверенному объему молекул в 1 моле газа:

,

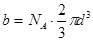(I.1.3)

.

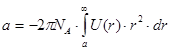(I.1.4)

Здесь N_A – число Авогадро, d – диаметр молекулы, U(r) – потенциальная энергия притяжения двух молекул.

Уравнение состояния Бертло (1900г.):

.

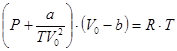(I.1.5)

Здесь а и b связаны с параметрами критического состояния (в критической точке) соотношениями [8]:

.

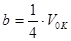(I.1.6)

Уравнение состояния Вукаловича и Новикова [7]:

.

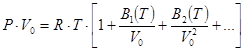(I.1.7)

Здесь B₁, B₂ и т.д. – так называемые вириальные коэффициенты весьма сложного вида. Их вычисление производится с учетом ассоциации молекул – объединения под влиянием ван-дер-ваальсовых сил притяжения.

Уравнение состояния Майера [7]:

,

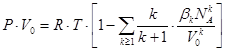(I.1.8)

где: 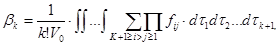 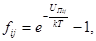       dt_i=dq_i1*...dq_in.

Здесь U_пij – взаимная потенциальная энергия i-й и j-й молекул, взаимодействующих по закону центральных сил, q_i1,......,q_in – обобщенные координаты i-той молекулы, обладающей n степенями свободы.

Уравнение Камерлинг-Оннеса (1901) [8]:

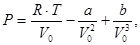
(I.1.9)

где        , .

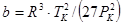Уравнение Редлиха-Квонга (1949 г.) [8]:

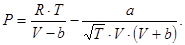
(I.1.10)

Здесь 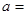0,42748·R²·T^2,5_k/P_k, b = 0,08664·R·T_k/P_k. Уравнение Редлиха-Квонга считается наилучшим двухконстантным уравнением. При его выводе авторы не руководствовались какими-то определенными теоретическими обоснованиями [8]. Это уравнение следует рассматривать как произвольную, но удачную эмпирическую модификацию предшествующих уравнений состояния.

Уравнение Мартина (1967 г.) [8]:

,

(I.1.11)

где 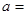 27·R²·T²_k/(64P_k), b = R·T_k/(8P_k).