В последнее время наблюдается рост интереса к различным термодинамическим эффектам в пористых средах. Это связано с их многообразными практическими приложениями[4,5].

Особую важность упомянутые проблемы имеют в физике нефтегазоносных пластов. Поля давления в нефтегазоносных пластах в условиях разработки, как правило, нестационарны. Дросселирование нефти и газа приводит к проявлению баротермического эффекта – изменению температуры при течении нефти или газа в пористой среде в нестационарном поле давления. Величина барометрического эффекта в отличие от эффекта Джоуля – Томсона, наблюдающегося при стационарном дросселировании, зависит от коллекторских свойств пористой среды, времени, геометрии течения и других факторов. Эти особенности баротермического эффекта обеспечивают возможность его практического применения при исследовании скважин и пластов.

В основу исследований положена полная система уравнений для 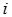- той фазы (компонента), описывающих баротермический эффект. Ядром этой системы является уравнение для температуры  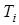с учетом термодинамических эффектов высокого порядка [9]

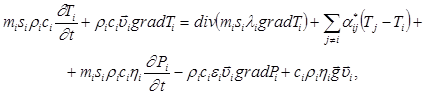
(I.2.1)

где первое слагаемое в левой части уравнения (I.2.1) описывает изменение температуры в пласте со временем, второе – за счет конвекции (перемещения больших объемов газа). Первое слагаемое в правой части ответственно за теплопроводность, второе – за межфракционный теплообмен, третье описывает адиабатический эффект, четвертое – эффект Джоуля-Томсона и пятое – влияние поля тяготения Земли.

Вторым уравнением системы является уравнение неразрывности, которое записывается в виде:

.

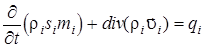(I.2.2)

Фильтрация газа подчиняется закону Дарси

.

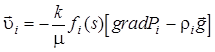(I.2.3)

К системе добавляется уравнение состояния

.

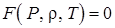(I.2.4)

Система (I.2.1)-(I.2.4) является нелинейной, кроме того, уравнения (I.2.1)-(I.2.2) являются взаимосвязанными.

Описание задачи

Рассмотрим температурную задачу в полярной системе координат, где среда представлена одной бесконечной областью (рис.1). Область является пористой и насыщена газом. Будем рассматривать случай радиального движения газа из бесконечности к скважине радиуса 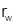, ось которой совпадает с осью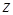

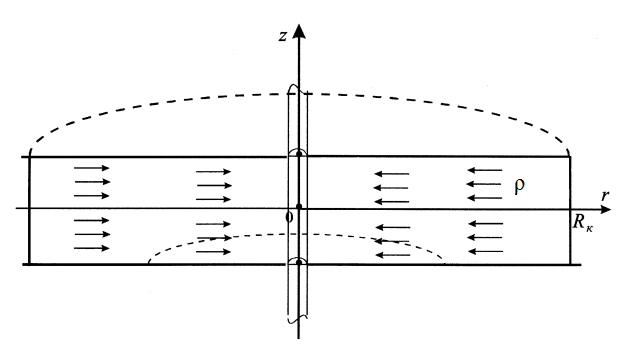
Рис. 1. постановка задачи

При описании температурной задачи примем следующие допущения:

- пористый пласт считается однородным и изотропным по гидродинамическим и теплофизическим свойствам;

- давления в скважине и на контуре питания остаются неизменными;

- породы, окружающие пласт предполагаются непроницаемыми и однородными по своим теплофизическим свойствам;

- температуры газа и скелета пористой среды в каждой точке совпадают;

- естественное тепловое поле Земли считается стационарным;

- пласт расположен на глубине порядка 1 – 2 км, поэтому суточные и сезонные колебания температуры не достигают пласта;

- адиабатическим эффектом, обусловленным гравитационным полем пренебрегаем.