Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Как было ранее показано (см. п. 2.1.), фактографические методы про­гнозирования можно условно разделить на две большие группы: статисти­ческие и методы аналогий.

Статистические методы прогнозирования

Статистические методы изучены лучше всего, однако не являются единственно возможными. В ряде случаев прибегают к построению сцена­риев развития, морфологическому анализу, историческим аналогиям. Но­вым подходом к прогнозированию НТП является, в частности, «симптома­тическое» прогнозирование, суть которого заключается в выявлении «предвестников» будущих сдвигов в технике и технологии. Однако в прак­тике экономики преобладающими по-прежнему являются статистические методы (что связано с наличием инерционности). Немаловажным является и то, что статистические методы опираются на аппарат анализа, развитие и практика которого имеют достаточно длительную историю.

Процесс статистического прогнозирования распадается на 2 этапа:

• Индуктивный, заключающийся в обобщении данных, наблюдаемых за более или менее продолжительный период времени, и в представлении соответствующих статистических закономерностей в виде модели. Про­цесс построения модели включает: выбор формы уравнения, описывающе­го динамику или взаимосвязь явлений; оценивание его параметров.

• Дедуктивный — собственно прогноз. На этом этапе определяют ожидаемое значение прогнозируемого показателя.

Не всегда статистические методы используются в чистом виде. Часто их включают в виде важных элементов в комплексные методики, преду­сматривающие сочетание статистических методов с другими, например, экспертными оценками.

Статистические методы основаны на построении и анализе динами­ческих рядов, либо данных случайной выборки. К ним относятся методы прогнозной экстраполяции, корреляционный и регрессионный анализ. В группу статистических методов можно включить метод максимального правдоподобия и ассоциативные методы — имитационное моделирование и логический анализ.

Динамику исследуемых показателей развития хозяйственной систе­мы можно прогнозировать при помощи двух различных групп количест­венных методов: методов однопараметрического и многопараметрического прогнозирования. Общим для обеих групп методов является, прежде всего, то, что применяемые для параметрического прогнозирования математиче­ские функции, основываются на оценке измеряемых значений прошедшего периода (ретроспективы). Однопараметрическое прогнозирование базиру­ется на функциональной зависимости между прогнозируемым параметрам (переменной) и его прошлым значением, либо фактором времени.

ŷ_t+1=ſ(y_t,y_t-1,…,y_t-n).                                                                       (2.1)

При обработке таких прогнозов пользуются методом экстраполяции трендов, экспоненциальным сглаживанием или авторегрессией.

В основе многопараметрических прогнозов лежит предположение о причинной взаимосвязи между прогнозируемым параметром и нескольки­ми другими независимыми переменными:

ŷ_t+1=f(x), или;                                                                                   (2.2)

ŷ_t+1=f(x₁, x₂,…, x_n).

Однопараметрические методы следует использовать при кратко­срочном (менее одного года) прогнозирования показателей, изменяющихся еженедельно или ежемесячно. Многопараметрические оправдывают себя для средне- и долгосрочного прогнозирования.

 

 

Да                                        нет                                         да                            нет

 

 

Нет                      

Инструмент прогноза   Скользящие и экспоненциаль- ные средние, ав- торегрессия

                                         да                             нет                                        да

 

 

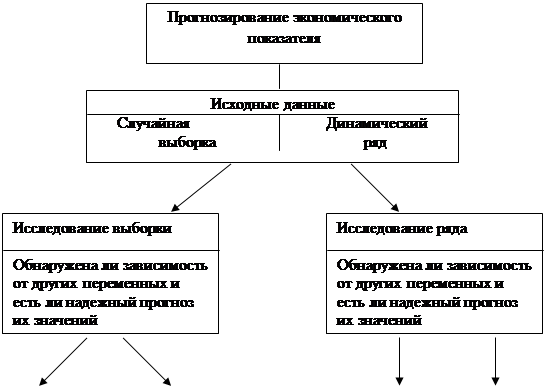
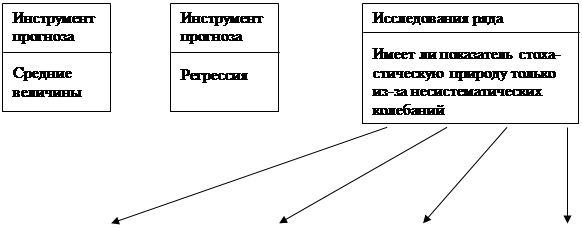
Рис.2.2.Схема выбора статистического метода прогнозирования

 

Выбор конкретного параметрического метода прогнозирования, кроме того, зависит от характера исходной статистической базы. В качест­ве исходных данных могут быть взяты выборочные наблюдения и динами­ческие ряды. В первом случае в качестве инструмента прогноза применя­ется регрессия. Значительно чаще, чем случайная выборка, информацион­ной базой для прогноза являются динамические ряды.

Тогда в качестве инструментов прогноза выступают тренды, авто­регрессия, смешанная авторегрессия и т.п. Выбор адекватного подхода за­висит от того, обнаружены ли экзогенные факторы, влияющие на значение зависимой переменной или нет, влияют ли на зависимую переменную предшествующие значения этой же переменной и т.д. В целом процесс вы­бора конкретного метода статистического параметрического прогнозиро­вания показан на рис. 2.2. [39].

Методы экстраполяции сводятся к обработке имеющихся данных об объекте прогнозирования за прошлое время и распространению обнару­женной в прошлом тенденции на будущее.

Методы моделирования — наиболее сложный метод прогнозирова­ния, состоящий из разнообразных подходов к прогнозированию сложных систем, процессов и явлений. Эти методы могут пересекаться и с эксперт­ными методами.

Экстраполяция трендов

Наиболее распространенными из группы математических методов являются методы прогнозной экстраполяции. Временной ряд при экстра­поляции представляется в виде суммы детерминированной (неслучайной) составляющей, называемой трендом, и стохастической (случайной) со­ставляющей, отражающей случайные колебания или шумы процесса.

Прогнозную экстраполяцию можно разбить на два этапа.

• Выбор оптимального вида функции, описывающей ретроспектив­ный ряд данных. Выбору математической функции для описания тренда предшествует преобразование исходных данных с использованием сгла­живания и аналитического выравнивания динамического ряда.

• Расчет коэффициентов (параметров) функции, выбранной для экст­раполяции.

Для оценки коэффициентов чаще остальных используется метод наименьших квадратов (МНК).

Сущность МНК состоит в отыскании коэффициентов модели тренда, минимизирующих ее отклонение от исходного временного ряда:

S = ∑(y_t - ŷ)² → min,                                                               (2.3)

где ŷ, - расчетные (теоретические) значения тренда;

у — фактические значения ретроспективного ряда;

n — число наблюдений.

Подбор модели в каждом конкретном случае осуществляется по це­лому статистически ряду критериев (дисперсии, корреляционному отно­шению и др.). Кроме того, для выбора зависимости

ŷ_t=f(t)

существует несколько подходов. Это метод последовательных разностей, метод характеристик прироста, визуальный (глазомерный) выбор формы. Расчет оценок прироста показателя, дополненный визуальным выбором взаимосвязи, уменьшает риск неправильного выбора модели для прогнози­рования. В частности, могут быть рекомендованы следующие аппрокси­мирующие зависимости:

∆ Y / ∆ t = const → ŷ_t =a₀ + a₁ t,                                                      (2.4)

∆ ln y / ∆ t = const → ŷ_t = a₀ t^a,                                                        (2.5)

∆ ln y / ∆ ln t = const → ŷ_t = a₀ t^t₁,                                                   (2.6)

∆ Y² / ∆ X² = const → ŷ_t = a₀ + a₁ t + a₂ t²,                                       (2.7)

∆ (t / y) / ∆ t = const → ŷ_t = t / (a₀ + a₁ t).                                          (2.8)

В Приложении 1 показаны графические зависимости, позволяющие осуществлять визуальный выбор формы зависимости прогнозируемого по­казателя от фактора времени, а в Приложении 2 - системы нормальных уравнений, применяемые для оценки параметров полиномов невысоких степеней.

Для выявления более четкой тенденции уровни, нанесенные на гра­фик, можно сгладить (элиминировать) с помощью трех приемов:

• метода технического выравнивания - когда на графике визуально (на глаз) проводится равнодействующая линия, отражающая на взгляд ис­следователя тенденцию развития;

• метода механического сглаживания - расчет скользящих и экспо­ненциальных средних;

• метода аналитического выравнивания - построение тренда.

Преимущество трендовой модели в более высокой степени надежно­сти. Кроме того, она позволяет экономически интерпретировать параметры уравнения тренда и достаточно наглядно изображает тенденцию и откло­нения от нее на графике.

В рыночной ситуации можно порекомендовать конкретные виды функций, наиболее пригодные для экстраполяции [29].

Спрос на ряд непродовольственных товаров может быть описан сте­пенной функцией или экспонентой (особенно на активных этапах жизнен­ного цикла товаров). Общие закономерности спроса отражаются кривой Гомперца. При изучении влияния фактора времени на спрос может быть использована логистическая (сигмоидальная) кривая. Процесс затухания роста спроса по мере перехода населения к группам населения с более вы­соким доходом отражается полулогарифмической кривой.

В развитии рынка как единого экономического пространства (как и в развитии локальных рынков) могут проявиться определенная повторяе­мость, цикличность, обусловленная как внутренними свойствами рынка, так и внешними причинами.

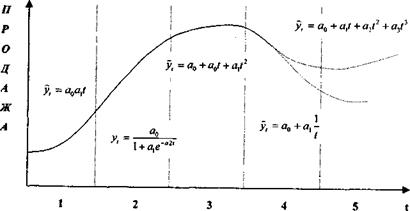
Рис. 2.3. Моделирование тенденции продажи товара по стадиям жизненного цикла

Условные обозначения:

1 - выведение товара на рынок; 2 - рост; 3 - зрелость; 4 - упадок; 5 - реанимация спроса.

Внутригодовая цикличность носит часто сезонный характер.

При изучении сезонных процессов часто применяется спектральный анализ, который позволяет прогнозировать тенденции, динамика которых содержит колебательные или гармонические составляющие [31].

Сезонные волны можно описать гармоникой ряда Фурье:

ŷ=α₀+∑^m_k(α_k coskt + b_k sinkt),                               (2.9)

где t - номер гармоники ряда Фурье;

а о и а k , bk — определяют по МНК;

k - число гармоник (1,2,...)

В условиях переходной экономики возрастает значимость прогнози­рования жизненного цикла товара (ЖЦТ). Автором концепции ЖЦТ счи­тается известный маркетолог Теодор Левитт, предложивший ее в 1965г.

Суть прогноза заключается в том, чтобы определить, как надолго и насколько интенсивно будет сохраняться спрос на данный товар. Прогноз ЖЦТ - многоплановый процесс, важной составляющей которого является подбор для каждого этапа соответствующей трендовой модели, отражаю­щей не только рост, стабилизацию или спад, но и степень ускорения или замедления этих процессов. Такой прогноз является составным элементом прогнозирования покупательного спроса и рыночной конъюнктуры.

Жизненный цикл товара можно графически смоделировать в виде сложной кривой (рис. 2.3).

Математически смоделировать весь жизненный цикл товара практи­чески невозможно, пришлось бы использовать сложную многочленную функцию, которую трудно интерпретировать. Целесообразно использовать метод линейно-кусочных агрегатов, то есть моделировать и прогнозиро­вать каждый этап ЖЦТ с помощью трендовой и (или) многофакторной мо­дели, отражающей закономерности каждого этапа.

Отмеченные ранее методы механического выравнивания могут так­же выступать в роли самостоятельных методов статистического прогнози­рования.

Прогнозирование на основе адаптивных скользящих средних произ­водится с использованием следующих формул:

 

M_i = M_i-1 + (y_i - y_i-m) / (m),                                                            (2.10)

где M_i – скользящая средняя, отнесенная к концу интервала.

 

M_i = ŷ_t = (∑^t+p_i=1 y_i) / (m).                                                             (2.11)

 

Первый член уравнения (2.10) – М_i-1 несет «груз прошлого» - инер­цию развития, а второй адаптирует среднюю к новым условиям. Таким об­разом, средняя как бы обновляется, «впитывая» информацию о фактически реализуемом процессе (степень обновления определяется весом 1/т).

Экспоненциальные средние. Влияние прошлых наблюдений должно затухать по мере удаления от момента, для которого определяется средняя. Для этой цели используют экспоненциальное сглаживание, применяемое в краткосрочном прогнозировании (идея Н.Винера):

Q_t = α · y_t + (1+α) · Q_t-1,                                                                     (2.12)

 

где Q_t - экспоненциальная средняя на момент t ;

а - коэффициент, характеризующий вес текущего наблюдения (параметр сглаживания).

При расчете по формуле (2.12) необходимо выбрать Q_t-1. Часто  

 Q_t-1 принимают равным y_t.

Применение метода успешно, когда ряд имеет достаточно большое число уровней. Чем меньше а, тем больше роль «фильтра», поглощающего колебания 0< а <1. Практически диапазон а ограничивается величинами 0,1; 0,3. Хорошие результаты дает а = 0,1. При выборе а следует иметь в виду, что для повышения скорости реакции на изменение процесса разви­тия необходимо повысить а, однако это уменьшает «фильтрационные» возможности средней.

Специфика экономических процессов состоит в том, что они обла­дают взаимосвязью и инерционностью (см. п. 1.3). Последнее означает, что значение фактического показателя в момент времени зависит определенным образом от состояния этого показателя в предыдущих периодах, т.е. значения прогнозируемого показателя должны рассматриваться как фак­торные признаки. Уравнение авторегрессионной зависимости в общем имеет вид:

 

ŷ_t = α₀ + α₁ · y_t-1 + α₂ · y_t-2 +...+ α_k · y_t-k,                                     (2.13)

 

где ŷ_t – прогнозируемые значения показателя в момент времени t;

y_{t-1 –} значения показателя y в момент времени (t-i);

α₁ – i-тый коэффициент регрессии.

Часто прогнозируемый показатель зависит не только от предшествующих состояний, но и от других факторов x. Тогда говорят о смешанной авторегрессии:

ŷ_t = α₁ · y_t-1 + α₂ · y_t-2 +...+ α_k · y_t-k + b₁ · x₁ + b₂ · x₂ +...+ b_m · x_m =

= ∑^k_i=1 α_i · y_t-I + ∑^m_j=1 b_j · x_j.                                                                  (2.14)

 

Оценки α_i и b_j находят по МНК.

Все приведенные выше модели позволяют получить точечные оценки. Для определения наиболее вероятных интервалов варьирования прогнозных показателей необходимо найти доверительные оценки. В общем виде расчет доверительного интервала может быть представлен следующим образом:

 

ŷ_t+a  ± t_a Sŷ,                                                                                          (2.15)

 

где ŷ_t+a  - точечный прогноз;

Sŷ – средняя квадратическая ошибка прогноза;

t_{a –} t-статистика Стьюдента;

α – период упреждения прогноза.

В общем виде для полиномов различных степеней:

Sŷ_t+2 = Sy √T`<sub>α</sub> (T` · T)^-1 · T_α,                                                             (2.16)

 

где (T` · T) – матрица системы нормальных уравнений;

Sy – среднее квадратическое отклонение фактических значений от расчётных.

В частности, для линейного тренда:

Sŷ = Sy √1 + 1 : n + (t_α - t)² : ∑(t')²,                                     (2.17)

 

Где t_{α –} заданное на период упреждения значение переменной t,

t – среднее значение t, т.е. значение порядкового номера уровня, стоящего в середине ряда;

∑(t')² – сумма квадратов отклонений значений независимой переменной от их средней.

Важно иметь в виду, что экстраполяция в рядах динамики носит приближенный и условный характер. Поэтому применение методов экст­раполяции не должно становиться самоцелью, а при разработке социально-экономических прогнозов должна привлекаться дополнительная информа­ция, на основе которой в полученные методом экстраполяции количест­венные оценки вносятся соответствующие коррективы.