Если заданная в промежутке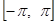 
функция 
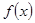будет нечетной, то очевидно
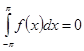
В этом легко убедится:
.
Таким же путем устанавливается, что в случае четной функции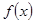 
:
.
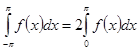Пусть теперь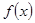 
будет кусочно-дифференцируемая в промежутке 
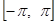четная функция. Тогда произведение 
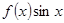окажется нечетной функцией, и по сказанному
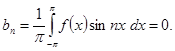
Таким образом, ряд Фурье четной функции содержит одни лишь косинусы:
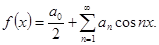(21)
Так как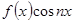 
в этом случае будет тоже четной функцией, то, применив сюда второе из сделанных выше замечаний, можем коэффициенты 
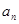разложения написать в виде
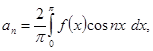
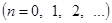(22)
Если же функция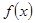 
будет нечетной, то нечетной будет и функция 
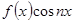, так что
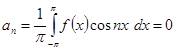
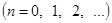
Мы приходим к заключению, что ряд Фурье нечетной функции содержит одни лишь синусы:
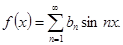(23)
При этом ввиду четности произведения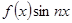 
можно писать:
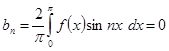
(24)
Отметим, что каждая функция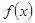 
, заданная в промежутке 
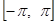, может быть представлена в виде суммы четной и нечетной составляющих функций:
,
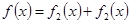Где
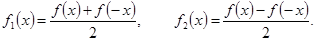
Очевидно, что ряд Фурье функции 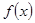как раз и составится из разложения по косинусам функции 
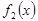и разложения по синусам функции 
.
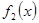Предположим, далее, что функция 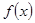задана лишь в промежутке 
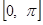. Желая разложить ее в этом промежутке в ряд Фурье мы дополним определение нашей функции для значений x в промежутке 
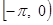по произволу, но с сохранением кусочной дифференцируемости, а затем применим сказанное в пункте «Случай непериодической функции».
Можно использовать произвол в определении функции в промежутке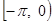 
так, что бы получить для 
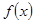разложение только лишь по косинусам или только по синусам. Действительно, представим семе, что для 
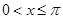мы полагаем 
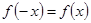, так что в результате получается четная функция в промежутке 
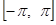. Ее разложение, как мы видели, будет содержать одни лишь косинусы. Коэффициенты разложения можно вычислять по формулам (22), куда входят лишь значения первоначально заданной функции 
.
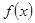Аналогично, если дополнить определение функции 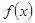по закону нечетности, то она станет нечетной и в ее разложении будут одни лишь синусы. Коэффициенты ее разложения определяются по формулам (24).
Таким образом, заданную в промежутке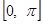 
функцию при соблюдении условий оказывается возможным разлагать как по косинусам, так и по одним лишь синусам.
Особого исследования требуют точк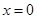и 
и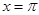 
. Здесь оба разложения ведут себя по-разному. Предположим, для простоты, что заданная функция 
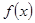непрерывна пр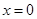и 
и 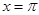, и рассмотрим сначала разложение по косинусам. Условие 
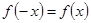, прежде всего, сохраняет непрерывность при 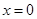, так что ряд (21) при 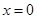будет сходиться именно к 
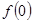. Так как, далее,
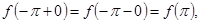
то и при 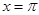имеет месть аналогичное обстоятельство.
Иначе обстоит дело с разложением по синусам. В точках 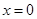и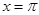 
сумма ряда (23) явно будет нулем. Поэтому она может дать нам значения 
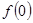и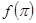 
, очевидно, лишь в том случае, если эти значения равны нулю.
Если функция 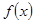задана в промежутке 
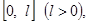то, прибегнув к той же замене переменной, что и в предыдущем параграфе, мы сведем вопрос о разложении ее в ряд по косинусам
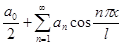
или в ряд по синусам
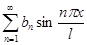
к только что рассмотренному. При этом коэффициенты разложений вычисляются, соответственно, по формулам
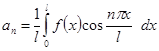
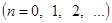
или
.
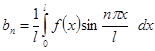
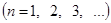Примеры разложения функций в ряд Фурье
Функции, которые ниже приводятся в качестве примеров, как правило, относятся к классу дифференцируемых или кусочно-дифференцируемых. Поэтому сама возможность их разложения в ряд Фурье—вне сомнения, и на этом мы останавливаться не будем.
Все задания взяты из Сборника задач и упражнений по математическому анализу, Б. Н. Демидович.
№ 2636. Функцию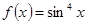 
разложить в ряд Фурье.
Так как функция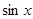 
является нечетной, то, следовательно, 
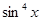будет четной. Поэтому ее разложение в ряд Фурье содержит одни лишь косинусы.
Найдем коэффициенты разложения;
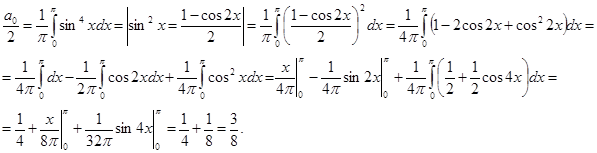
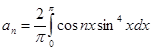
№ 2938. Разложить в ряд Фурье функцию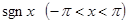 
. Изобразить этой функции и графики нескольких частных сумм ряда Фурье этой функции.
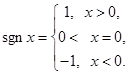
Функция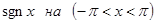 
нечетная, поэтому ее разложение будет содержать одни лишь синусы.
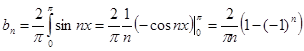
То есть, получается, что при четных значениях n коэффициент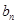 
, а следовательно и все слагаемое, обращается в нуль. Поэтому суммирование идет только лишь по четным значениям n.
Ряд Фурье для этой функции примет следующий вид:
. 
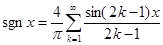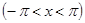
Ниже изображены графики функций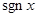 
и нескольких частных сумм ряда Фурье:
График функци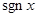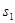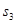и , 
, 
и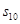 
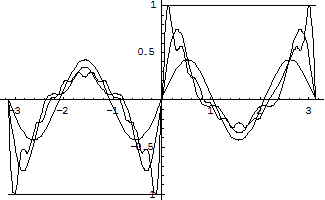
№ 2940.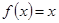 
в интервале 
.
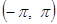Функция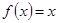 
нечетная.
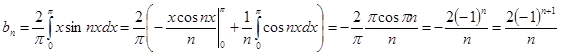
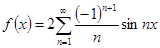
№ 2941. 
в интервале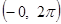 
.
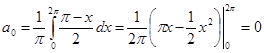
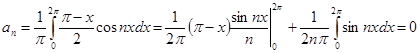
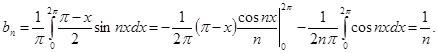
В итоге получаем ряд Фурье:
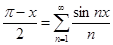
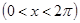
№ 2941.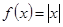 
в интервале 
.
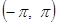Функция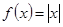 
четная.
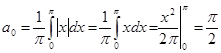
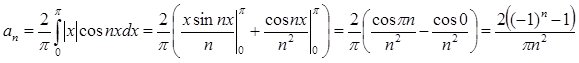
Как и в № 2938, у нас при четных значениях n коэффициент 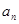обращается в нуль. Поэтому суммировать будем лишь по нечетным значениям.
В итоге получим:
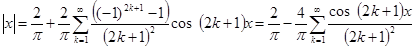
№ 2950.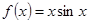 
в интервале .
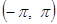Функция 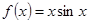четная.
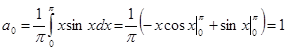
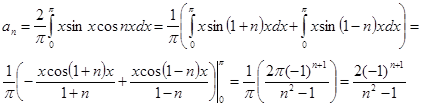
Так как при n=1 знаменатель обращается в нуль, то суммирование необходимо произвести начиная в двойки.
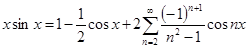
№ 2951.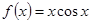 
в интервале 
.
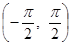Функция 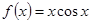нечетная.
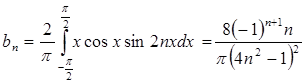
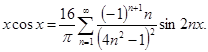
№ 2961. Функцию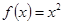 
разложить а) в интервале 
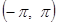по косинусам кратных дуг; б) в интервале 
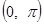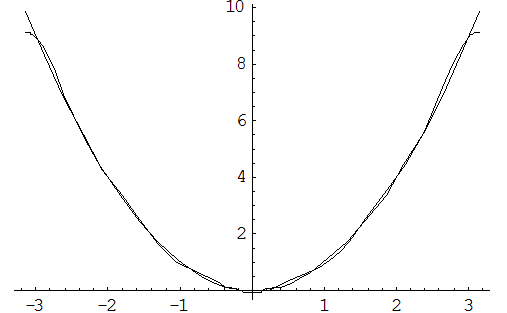
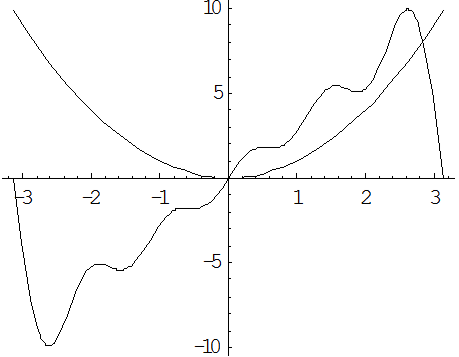
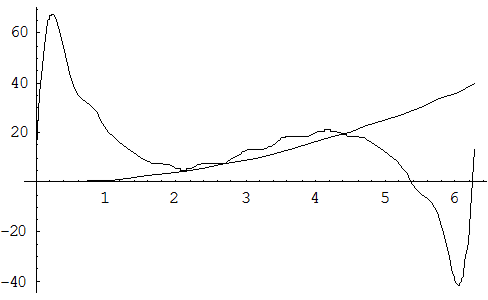
по синусам кратных дуг; в) в интервале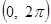 
. Изобразить график функции 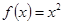и сумм рядов Фурье для каждого отдельного случая. Используя разложения, найти суммы рядов: 
; 
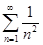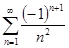и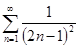 
.
а)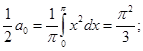 
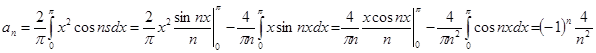
И, наконец получаем разложение в ряд Фурье:
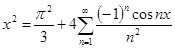
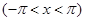
б)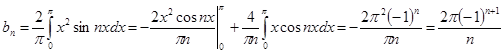 
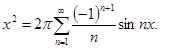
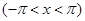
в)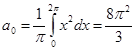 
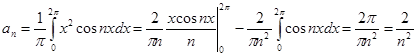
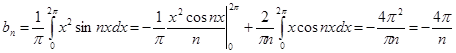
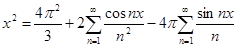
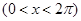
№ 2962 Исходя из разложения
,
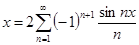
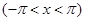почленным интегрированием получить разложение в ряд Фурье на интервале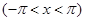 
функций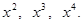 
Проинтегрируем равенство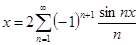 
почленно, получим
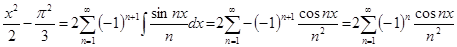
И окончательно получаем:
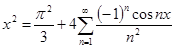
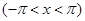
Проинтегрируем полученное равенство повторно
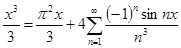
или отсюда получаем
.
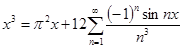Список использованной литературы
1 И.М. Уваренков, М.З. Маллер „Курс математического анализа”, М., „Просвещение”, 1976 г.
2 Г.М. Фихтенгольц „Курс дифференциального и интегрального исчисления”, том III, издание 8, М., „ФИЗМАТЛИТ”, 2005г.
3 В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов „Краткий курс высшей математики”, том2, М., „Высшая школа”, 1978г.
4 Н.Я. Виленкин, В.В. Цукерман, М.А. Доброхотова, А.Н. Сафонов „Ряды”, М. „Просвещение”, 1982г.
5 Б.П. Демидович „Сборник задач и упражнений по математическому анализу” издание 9, М. „Наука”, 1977г.
Дата: 2019-07-31, просмотров: 216.
