В предыдущем параграфе было сказано, что существует ряд функций, которые можно представить в виде бесконечного тригонометрического ряда. Для того, что бы установить возможность разложения некоторой функции 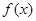, имеющей период 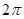в тригонометрический ряд вида:

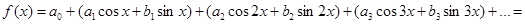
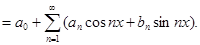 (4)

нужно иметь набор коэффициентов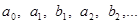

Прием для нахождения этих коэффициентов во второй половине XVIII века был применен Эйлером и независимо от него в начале XIX века—Фурье.

Впредь будем предполагать функцию 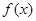непрерывной или кусочнонепрерывной в промежутке .

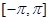Допустим, что разложение (4) имеет место. Проинтегрируем его почленно от 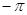до 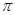; в результате получим:

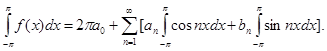
Но, как легко видеть,

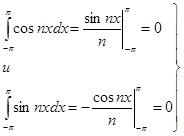 (5)

Поэтому все члены под знаком суммы будут равняться нулю, и окончательно получаем

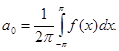 (6)

Для того чтобы найти значение коэффициента 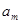, умножим обе части равенства (4) на  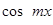и снова проинтегрируем почленно в том же промежутке:

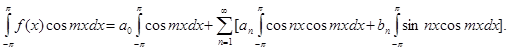
В виду (5) .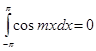

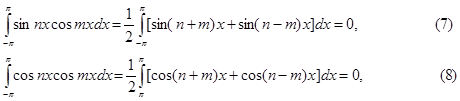
если 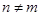, и, наконец,

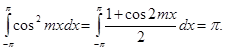 (9)

Таким образом, обращаются в нуль все интегралы под знаком суммы, кроме интеграла, при котором множителем стоит именно коэффициент 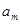. Отсюда получаем:

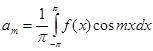
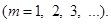
Аналогично, умножая разложение (4) на 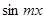и затем, интегрируя почленно, определим коэффициент при синусе:

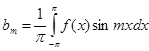
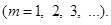
Формулы, по которым вычисляются коэффициенты 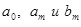, называются формулами Эйлера-Фурье, а сами коэффициенты называются коэффициентами Фурье для данной функции. И, наконец, тригонометрический ряд (4), составленный по этим коэффициентам, получил название ряд Фурье для данной функции.

Дадим теперь отчет в том, какова логическая ценность проведенных рассуждений. Мы исходили из того, что тригонометрический ряд (4) имеет место, поэтому вопрос о том, отвечает ли это действительности, остается открытым. Мы пользовались повторно почленным интегрированием ряда, а эта операция не всегда дозволительна, достаточным условием для применения операции является равномерная сходимость ряда. Поэтому строго установленным условием можно считать лишь следующее:

если функция f(x) разлагается в равномерно сходящийся тригонометрический ряд (4), то этот ряд будет являться ее рядом Фурье.

Если же не предполагать наперед равномерности сходимости, то все приведенные выше соображения не доказывают даже того, что функция может разлагаться только в ряд Фурье. Эти рассуждения можно рассматривать лишь как наведение, достаточное для того, чтобы в поисках тригонометрического разложения данной функции начать ее с ряда Фурье, обязуясь установить условия, при которых он сходится и притом именно к данной функции.

Пока этого не сделано, мы имеем право лишь формально рассматривать ряд Фурье данной функции, но не можем о нем ничего утверждать, кроме того, что он «порожден» функцией f(x). Эту связь обычно обозначают так:

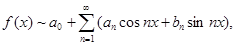
 избегая знака равенства.