Курсовая работа
«Ряды Фурье»
Выполнил: Студент 131 группы
Гаврутенко А.В.
Научный руководитель: профессор кафедры фундаментальной и прикладной математики,
теории и методики обучения математике
Менчер А.Э.
Чита 2009
Оглавление
Введение
Определение коэффициентов по методу Эйлера-Фурье
Ортогональные системы функций
Интеграл Дирихле Принцип локализаци
Представление функций рядом Фурье
Случай непериодической функции
Случай произвольного промежутка
Случай четных и нечетных функций
Примеры разложения функций в ряд Фурье
Список использованной литературы
Введение
В науке и технике часто приходиться иметь дело с периодическими явлениями, т. е. такими, которые воспроизводятся в прежнем виде через определенный промежуток времени Т, который называется периодом. Например, движение паровой машины повторяется, после того как пройдет полный цикл. Различные величины, связанные с периодическим явлением, по истечении периода Т возвращаются к своим прежним значениям и представляют собой периодические функции от времени t с периодом Т.
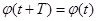
Если не считать постоянной, то простейшей периодической функцией является синусоидальная величина: 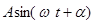 , где
, где 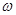 есть частота, связанная с периодом Т соотношением:
есть частота, связанная с периодом Т соотношением:
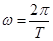 .
.
Из подобных простейших периодических функций могут быть составлены и более сложные. Ясно, что составляющие синусоидальные величины должны быть разных частот, иначе их сложение не дает ничего нового, а вновь приводит к синусоидальной величине, причем той же частоты. Если же сложить величины вида:
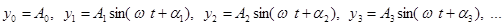 (1)
(1)
которые имеют разные частоты
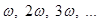 ,
,
то получится периодическая функция, но уже существенно отличающаяся от величин, входящих в сумму.
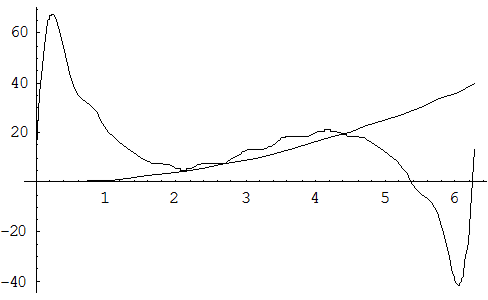
Рассмотрим для примера сложение трех синусоидальных величин:
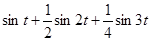
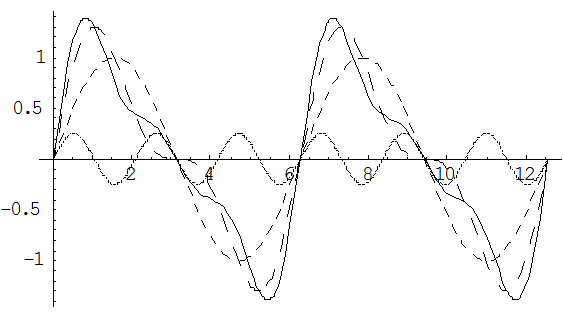
На рисунке мы видим, что график функции полученной в результате сложения трех синусоидальных величин (показан сплошной линией) уже значительно отличается от синусоиды. В большей степени это имеет место для суммы бесконечного ряда величин вида (1).
Теперь возникает обратный вопрос: можно ли данную периодическую функцию представить в виде суммы конечного или бесконечного множества синусоидальных величин вида (1).
Как будет показано ниже, на этот вопрос можно ответить удовлетворительно, но только лишь используя бесконечную последовательность величин вида (1). Для функций некоторого класса имеет место разложение в «тригонометрический ряд»:
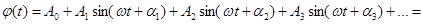
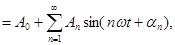 (2)
(2)
С геометрической точки зрения это означает, что график периодической функции получается путем наложения ряда синусоид. Если же каждую синусоидальную величину истолковать механически как представляющую гармонические колебательные явления, то можно сказать, что здесь сложное колебание разлагается на отдельные гармонические колебания. Исходя из этого, отдельные синусоидальные величины, входящие в состав разложения (2), называют гармоническими составляющими функции 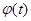 или просто ее первой, второй и т. д. гармониками. Сам же процесс разложения периодической функции на гармоники носит название гармонического анализа.
или просто ее первой, второй и т. д. гармониками. Сам же процесс разложения периодической функции на гармоники носит название гармонического анализа.
Если за независимую переменную выбрать
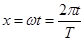 ,
,
то получиться функция, зависящая от х, так же периодическая, но уже со стандартным периодом 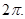 Разложение (2) в этом случаи примет вид:
Разложение (2) в этом случаи примет вид:

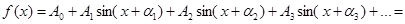
 (3)
(3)
Теперь развернув члены этого ряда по формуле синуса суммы и обозначив
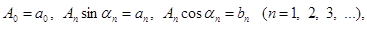
мы придем к окончательной форме тригонометрического разложения:

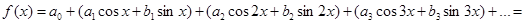
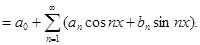 (4)
(4)
В данном разложении функция от угла х, имеющая период 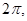 разложена по косинусам и синусам углов, кратных х.
разложена по косинусам и синусам углов, кратных х.
Мы пришли к разложению функции в тригонометрический ряд, отправляясь от периодических, колебательных явлений и связанных с ними величин. Подобные разложения часто оказываются полезными и при исследовании функций, заданных в определенном конечном промежутке и вовсе не порожденных никакими колебательными явлениями.
Примеры разложения функций в ряд Фурье
Функции, которые ниже приводятся в качестве примеров, как правило, относятся к классу дифференцируемых или кусочно-дифференцируемых. Поэтому сама возможность их разложения в ряд Фурье—вне сомнения, и на этом мы останавливаться не будем.
Все задания взяты из Сборника задач и упражнений по математическому анализу, Б. Н. Демидович.
№ 2636. Функцию 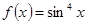 разложить в ряд Фурье.
разложить в ряд Фурье.
Так как функция 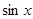 является нечетной, то, следовательно,
является нечетной, то, следовательно, 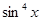 будет четной. Поэтому ее разложение в ряд Фурье содержит одни лишь косинусы.
будет четной. Поэтому ее разложение в ряд Фурье содержит одни лишь косинусы.
Найдем коэффициенты разложения;
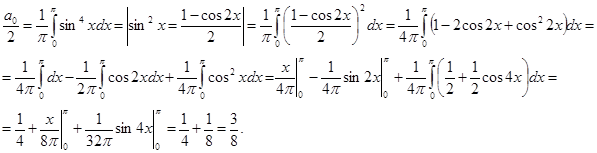
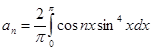
№ 2938. Разложить в ряд Фурье функцию 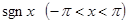 . Изобразить этой функции и графики нескольких частных сумм ряда Фурье этой функции.
. Изобразить этой функции и графики нескольких частных сумм ряда Фурье этой функции.
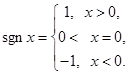
Функция 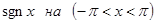 нечетная, поэтому ее разложение будет содержать одни лишь синусы.
нечетная, поэтому ее разложение будет содержать одни лишь синусы.
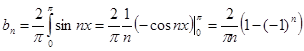
То есть, получается, что при четных значениях n коэффициент 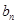 , а следовательно и все слагаемое, обращается в нуль. Поэтому суммирование идет только лишь по четным значениям n.
, а следовательно и все слагаемое, обращается в нуль. Поэтому суммирование идет только лишь по четным значениям n.
Ряд Фурье для этой функции примет следующий вид:
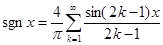 .
. 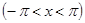
Ниже изображены графики функций 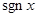 и нескольких частных сумм ряда Фурье:
и нескольких частных сумм ряда Фурье:
График функции 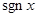 ,
, 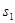 ,
, 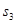 и
и 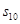
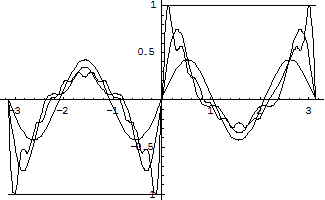
№ 2940. 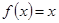 в интервале
в интервале 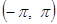 .
.
Функция 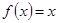 нечетная.
нечетная.
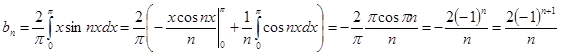
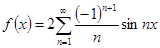
№ 2941.  в интервале
в интервале 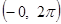 .
.
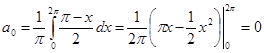
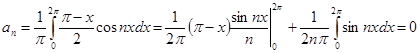
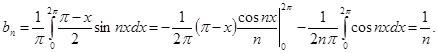
В итоге получаем ряд Фурье:
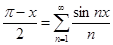
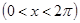
№ 2941. 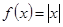 в интервале
в интервале 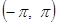 .
.
Функция 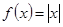 четная.
четная.
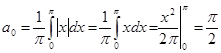
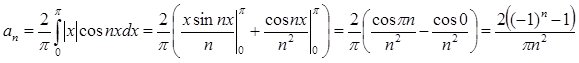
Как и в № 2938, у нас при четных значениях n коэффициент 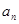 обращается в нуль. Поэтому суммировать будем лишь по нечетным значениям.
обращается в нуль. Поэтому суммировать будем лишь по нечетным значениям.
В итоге получим:
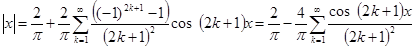
№ 2950. 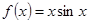 в интервале
в интервале 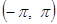 .
.
Функция 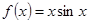 четная.
четная.
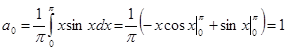
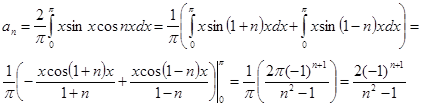
Так как при n=1 знаменатель обращается в нуль, то суммирование необходимо произвести начиная в двойки.
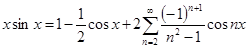
№ 2951. 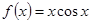 в интервале
в интервале 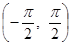 .
.
Функция 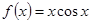 нечетная.
нечетная.
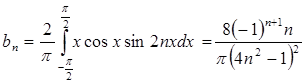
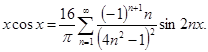
№ 2961. Функцию 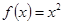 разложить а) в интервале
разложить а) в интервале 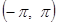 по косинусам кратных дуг; б) в интервале
по косинусам кратных дуг; б) в интервале 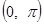 по синусам кратных дуг; в) в интервале
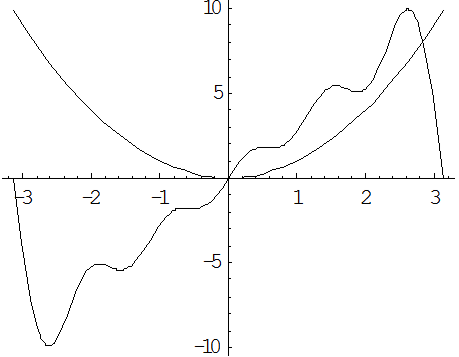
по синусам кратных дуг; в) в интервале 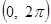 . Изобразить график функции
. Изобразить график функции 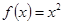 и сумм рядов Фурье для каждого отдельного случая. Используя разложения, найти суммы рядов:
и сумм рядов Фурье для каждого отдельного случая. Используя разложения, найти суммы рядов: 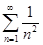 ;
; 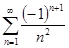 и
и 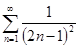 .
.
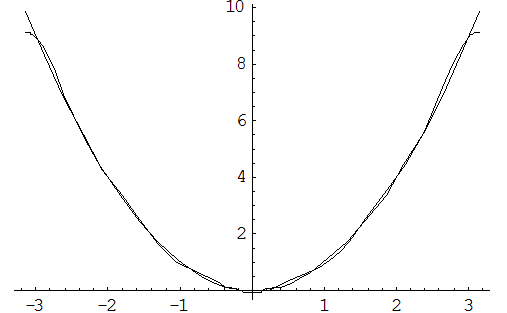
а) 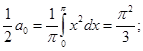
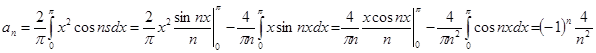
И, наконец получаем разложение в ряд Фурье:
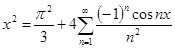
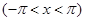
б) 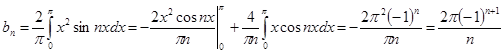
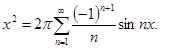
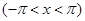
в) 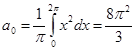
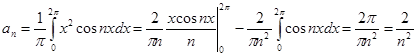
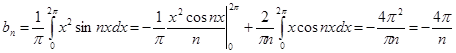
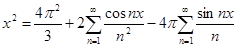
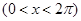
№ 2962 Исходя из разложения
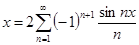
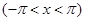 ,
,
почленным интегрированием получить разложение в ряд Фурье на интервале 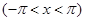 функций
функций 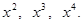
Проинтегрируем равенство 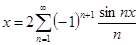 почленно, получим
почленно, получим
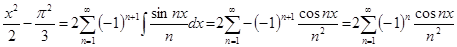
И окончательно получаем:
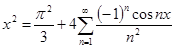
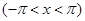
Проинтегрируем полученное равенство повторно
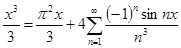
или отсюда получаем
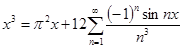 .
.
Список использованной литературы
1 И.М. Уваренков, М.З. Маллер „Курс математического анализа”, М., „Просвещение”, 1976 г.
2 Г.М. Фихтенгольц „Курс дифференциального и интегрального исчисления”, том III, издание 8, М., „ФИЗМАТЛИТ”, 2005г.
3 В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов „Краткий курс высшей математики”, том2, М., „Высшая школа”, 1978г.
4 Н.Я. Виленкин, В.В. Цукерман, М.А. Доброхотова, А.Н. Сафонов „Ряды”, М. „Просвещение”, 1982г.
5 Б.П. Демидович „Сборник задач и упражнений по математическому анализу” издание 9, М. „Наука”, 1977г.
Курсовая работа
«Ряды Фурье»
Выполнил: Студент 131 группы
Гаврутенко А.В.
Научный руководитель: профессор кафедры фундаментальной и прикладной математики,
теории и методики обучения математике
Менчер А.Э.
Чита 2009
Оглавление
Введение
Определение коэффициентов по методу Эйлера-Фурье
Дата: 2019-07-31, просмотров: 350.