Пусть 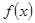 будет непрерывная или кусочно-непрерывная функция с периодом 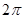. Вычислим постоянные (ее коэффициенты Фурье):

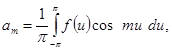
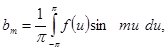
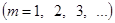
и по ним составим ряд Фурье нашей функции

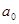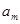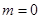Как видим, здесь коэффициент  мы определили по общей формуле для  при , но зато свободный член ряда запишем в виде .

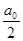Если функция F(x) кусочно-непрерывна в любом конечном промежутке и к тому же имеет период 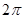, то величина интеграла

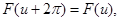
по прежнему промежутку длины 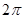 не зависит от .

Действительно, имеем

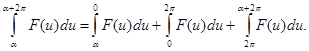
Если в последнем интеграла сделать подстановку 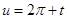, то он приведется к интегралу

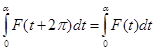
и лишь знаком будет отличаться от первого интеграла. Таким образом, рассматриваемый интеграл оказывается равным интегралу

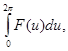
уже не содержащему .

Для того чтобы исследовать поведение ряда в какой-нибудь определенной точке 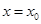, составим удобное выражение для его частичной суммы

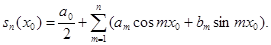
Подставим вместо 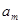 и 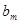 их интегральные выражения и подведем постоянные числа  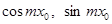под знак интеграла:

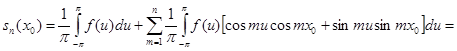
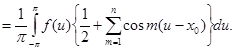
Легко проверить тождество

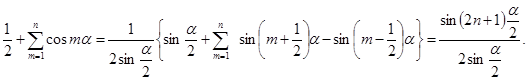
Воспользуемся этим тождеством для преобразования подынтегрального выражения, окончательно получим

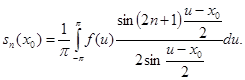 (13)

Этот интеграл называют интегралом Дирихле, хотя у Фурье он встречается гораздо раньше.

Так как мы имеем дело с функцией от u периода 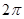, то промежуток интегрирования  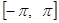по сделанному выше замечанию можно заменить, например, промежутком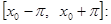

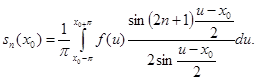
Подстановкой 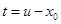 преобразуем этот интеграл к виду

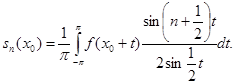
Затем, разбивая интеграл на два: 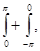 и приводя второй интеграл путем замены знака переменной тоже к промежутку 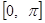, придем к такому окончательному выражению для частичной суммы ряда Фурье:

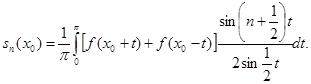 (14)

Таким образом, дело сводится к исследованию поведения именно этого интеграла, содержащего параметр n.

Для дальнейшего изложения материала нам потребуется одна лемма, принадлежащая Риману, которую мы оставим без доказательства.

Если функция  непрерывна или кусочно-непрерывна в некотором конечном промежутке 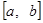, то

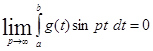
и, аналогично,

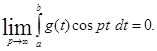
Если вспомнить формулы, выражающие коэффициенты Фурье 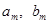, то в качестве первого непосредственного следствия из леммы получается утверждение:

Коэффициенты Фурье 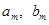 кусочно-непрерывной функции при  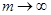стремятся к нулю.

Вторым непосредственным следствием является так называемый «принцип локализации».

Взяв произвольное положительное число 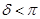, разобьем интеграл в (14) на два: 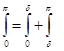. Если второй из них переписать в виде

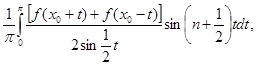
то станет ясно, что множитель при синусе

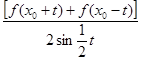
является кусочно-непрерывной функцией от t в промежутке 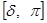. В этом случае по лемме этот интеграл при  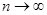стремится к нулю, так что и само существование предела для частичной суммы ряда Фурье и величина этого предела целиком определяется поведением одного лишь интеграла

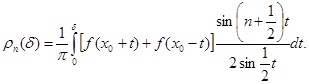
Но в этот интеграл входят лишь значения функции f(x), отвечающие изменению аргумента в промежутке от 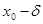 до 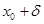. Этим соображением доказывается «принцип локализации», состоящий в следующем:

Поведение ряда Фурье функции f(x) в некоторой точке 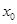 зависит исключительно от значений, принимаемых этой функцией в непосредственной близости рассматриваемой точки, т. е. в сколь угодно малой ее окрестности.

Таким образом, если взять две функции, значения которых в произвольно малой окрестности 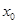 совпадают, то как бы они не расходились вне этой окрестности, соответствующие этим функциям ряды Фурье ведут себя в точке  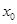одинаково: либо оба сходятся, и притом к одной и той же сумме, либо оба расходятся.